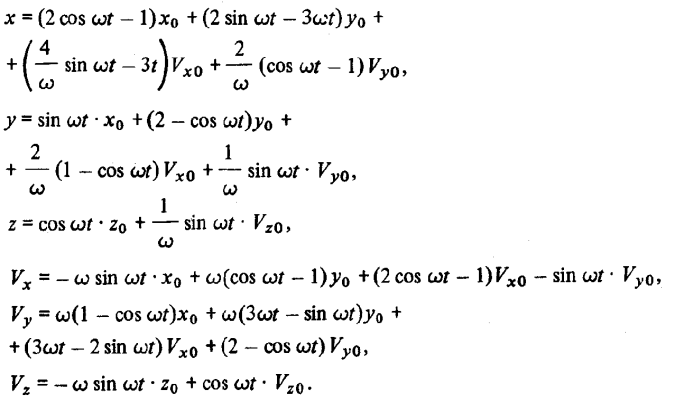Траектория относительно опорного движения. Смещение движения

Пользуясь свойством независимости плоского и бокового движений в решении (2.6), рассмотрим геометрию движения ЛА в плоскости опор­ной орбиты. Для этого сгруппируем члены первых двух уравнений (2.6) следующим образом:

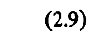
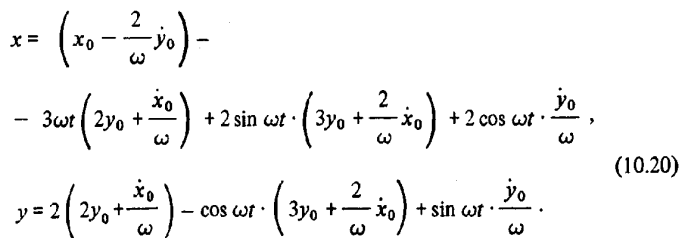
Введем величину 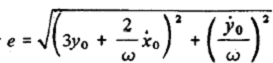и заметим, что всегда можно найти такое значение некоторого угла 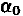что

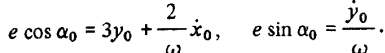
Теперь уравнения (2.9), описывающие траекторию относительного движения, приводятся к виду

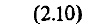
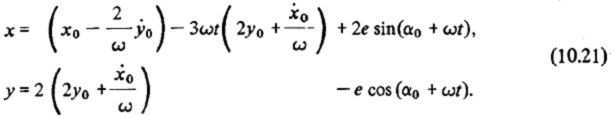
Выделим слагаемые:

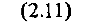
характеризующие движение по эллипсу, и слагаемое, характеризующее движение центра эллипса параллельно оси х со скоростью

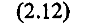
причем в начальный момент времени t = 0 центр эллипса имеет координаты

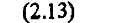
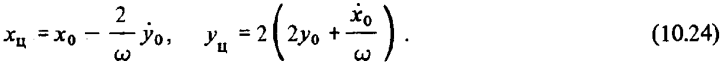
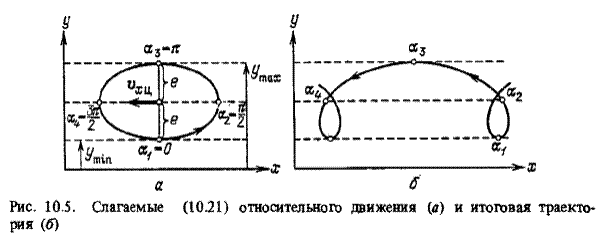
Величина полуоси эллипса вдоль оси Ох вдвое больше величины полуоси вдоль оси Оу и движение по эллипсу происходит против направления движения часовой стрелки, причем началом отсчета угла а является луч, исходящий из центра эллипса в направлении, обратном направлению оси Оу.

Центр эллипса может лежать выше и ниже опорной орбиты - его положение определяется знаком скобки 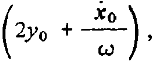который определяет и направление скорости смещения эллипса вдоль оси Ox: при 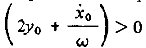центр лежит выше орбиты, а скорость его смещения отрицательна, в противном случае – наоборот. При 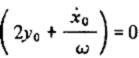центр лежит на оси Оx и не смещается в течении времени.

Из второго уравнения (5.21) определяются максимальные и минимальные смещения по высоте относительно опорного движения

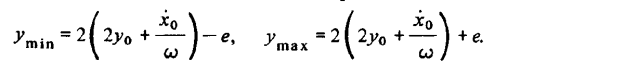
На рис. 2.3,а изображено движение по эллипсу согласно (2.11), на рис. 2.5, б — суммарное движение в соответствии с (2.10).

Говоря об относительном движении, не будем забывать, что каждый из двух летательных аппаратов движется по кеплеровой орбите, причем опорная орбита является круговой, а другая орбита, — вообще говоря, эллиптической. Будем называть вторую орбиту возмущенной и установим связь между параметрами относительного движения и кеплеровыми эле­ментами возмущенной орбиты.

Поскольку опорное движение происходит по круговой орбите радиу­са R, можно определить перигейное и апогейное расстояния возмущен­ной орбиты, соответствующие экстремальным высотам относительного движения:

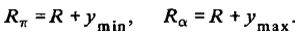
Зная 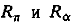возмущенной орбиты, нетрудно определить ее большую полуось

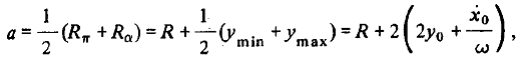
т.е. от большой полуоси опорной орбиты 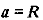большая полуось возмущенной орбиты отличается на 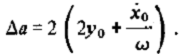Заметим, что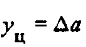

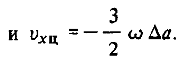
Поскольку при изменении большой полуоси орбиты на 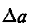ее период в линейном приближении меняется на величину

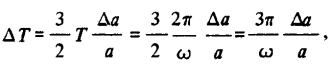
то период возмущенной орбиты отличается от периода опорного движения 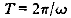на величину

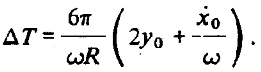
Вектор эксцентриситета.

Рассмотрим более подробно величину е, которая по компонентам вектора состояния 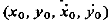в момент 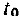определяется формулой

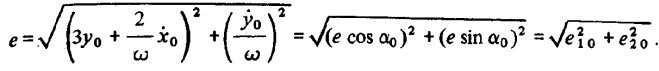
Если мы спрогнозируем вектор состояния на момент 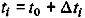и по компонентам нового вектора состояния вновь определим е, то получим

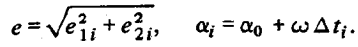
Существенным является то, что величина е для относительного движения, заданного начальным вектором состояния, постоянна, хотя ее компоненты 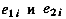меняются во времени:

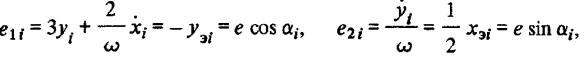
т.е. 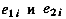можно трактовать как компоненты вектора е, модуль которо­го постоянен, а направление относительно осей Ох и Оу характеризуется переменным углом отсчитываемым в соответствии с рис. 2.2.

Вектор е вращается в ОСК с угловой скоростью изменения угла 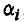, т.е. со скоростью 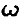. Заметим, что относительно инерциального пространства орбитальная СК (или цилиндрическая СК) вращается также с угловой ско­ростью 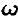, но в направлении, обратном направлению вращения вектора е. Следовательно, можно утверждать, что направление вектора е неизменно в инерциальном пространстве и изменение его проекций в ОСК происходит только за счет вращения самой ОСК.

Для того чтобы понять, как расположен вектор е относительно кеплеро­вой возмущенной орбиты в инерциальном пространстве, заметим, что при 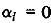достигается перигей 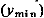,а при возмущен­ной орбиты. Но при 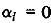имеем 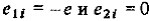,т.е. – вектор е в момент прохождения перигея направлен противоположно оси Оу (рис. 2.5). Как следует из рисунка, угол 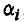фактически равен фазовому углу, который пройден ЛА по возмущенной орбите от момента последнего прохождения перигея, т.е. он равен истинной аномалии ЛА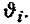

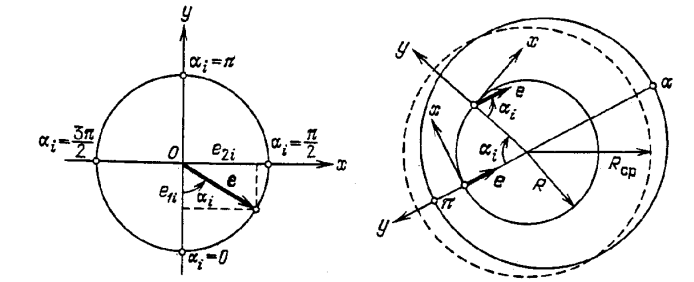
Рис. 2.4. Вектор эксцентриситета в декартовой объектоцентрической системе коор­динат.

Рис. 2.5. Положение вектора эксцентриситета относительно кеплеровой возмущен­ной орбиты.

Вектор е имеет размерность длины и в соответствии с ранее полученны­ми результатами его компонента 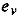характеризует высотный сдвиг возму­щенного движения относительно круговой орбиты, радиус которой равен большой полуоси возмущенной орбиты

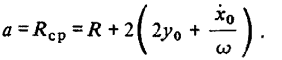
Выражения для перигейного и апогейного расстояний возмущенной орбиты могут быть теперь записаны в виде

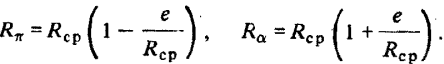
Из кеплеровой теории известны соотношения

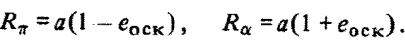
Сравнение выражений для 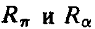, полученных при рассмотрении отно­сительного движения и в кеплеровой теории, сразу определяет зависимость между эксцентриситетом относительного движения е и кеплеровым эксцен­триситетом :

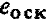2.7. Уравнения прогноза относительного движения двух ЛА, каж­дый из которых движется по эллиптической орбите.

До сих пор, говоря об относительном движении двух ЛА, мы полагали, что орбита одного из них является круговой. Можно ли использовать полу­ченные результаты для описания относительного движения двух ЛА, каж­дый из которых движется по эллиптической орбите? Оказывается можно, и эта возможность предоставляется нам благодаря тому, что мы рассмотре­ли относительное движение в линейном приближении. Действительно, пусть два ЛА движутся по эллиптическим орбитам и пусть для обоих ЛА можно указать такое фиктивное опорное круговое движение и такую связанную с ним орбитальную систему координат, что будут выполняться все необхо­димые условия для решения задачи в линейном приближении, т.е. соот­ветствующие отклонения координат обоих ЛА от начала системы отсчета будут достаточно малы (это одновременно означает и малость рассогласо­ваний координат самих ЛА). Для каждого ЛА мы вправе записать уравне­ние прогноза:

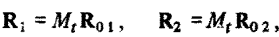
где 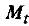- матрица прогноза, элементы которой являются функциями време­ни прогноза и угловой скорости опорного движения; - векторы состояния относительных движений летательных аппаратов в начальный момент времени; 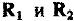— векторы состояния относительных движений летательных аппаратов в конечный момент времени. Из разности этих уравнений нетрудно получить

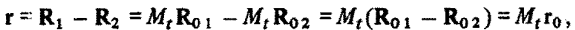
где 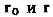— векторы состояния движения первого ЛА относительно второ­го соответственно в начальный и конечный моменты времени.

Естественно, что при указанном относительном движении невозможно установить простую связь между параметрами относительного движения и кеплеровыми элементами, поскольку 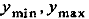и е в этом случае харак­теризуют возмущение не круговой, а эллиптической орбиты.

Завершая описание линейной теории относительного движения, остано­вимся на свойствах матрицы прогноза 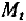, уравнения (2.18). Запишем это уравнение в виде

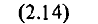
Где 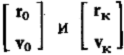векторы состояния относительного движения соответственно в начальный момент 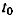и конечный момент 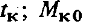— матрица, осуществляющая прогноз вектора состояния на временной интер­вал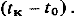

Получим вектор состояния в момент 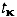иным образом, осуществив сначала прогноз на промежуточный момент 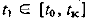и продолжив его затем до момента :

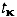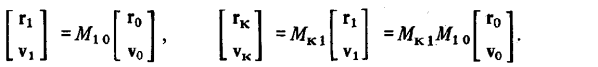
Таким образом, результирующая матрица прогноза 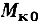на временной интервал 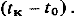есть результат произведения матриц прогноза 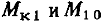при осуществлении прогноза последовательно на интервал 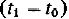и затем на интервал 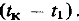Этот вывод можно обобщить следующим образом:

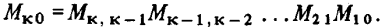
До сих пор рассматривался прогноз вектора состояния относительного движения на некоторый момент в будущем, но, очевидно, прогноз может быть осуществлен и на заданный момент в прошлом — для этого достаточно определить элементы матрицы прогноза 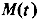для отрицательного времен­ного интервала. При этом

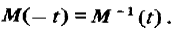
При решении ряда задач может оказаться более удобным рассматривать относительное движение в какой-либо системе координат, отличающейся от использованных нами орбитальных вращающихся систем (ОСК или ЦСК). Если преобразование вектора состояния R при переходе к новой системе координат является линейным и задается постоянной матрицей А 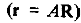, то легко получить матрицу прогноза относительного движения в новой системе координат:

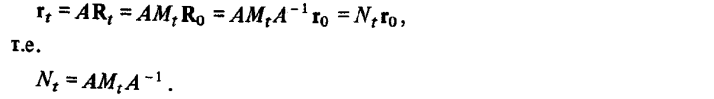
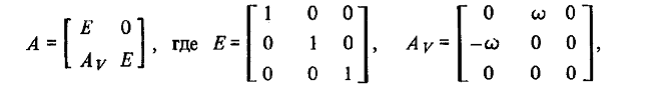В качестве примера подобного преобразования укажем на преобразова­ние "замораживания" вектора состояния, заданного в ОСК. В результате такого преобразования мы приходим к ОСКЗ (ОСК "замороженная"), оси которой в любой момент времени совпадают с осями ОСК и вместе с тем в каждый текущий момент неподвижны относительно инерциального пространства. Матрицу А этого преобразования можно представить в блочном виде

а результат преобразования вектора состояния R, заданного в ОСК, — в виде

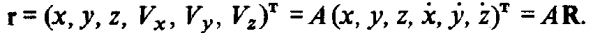
Исходя из характера преобразования, можно сказать, что вектор состоя­ния r есть результат проектирования разности абсолютных векторов состояния возмущенного и опорного движений на оси ОСК.

Матрица прогноза 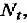полученная по формуле 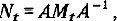дает следую­щий аналог решения (2.6) для ОСКЗ: