Основные расчетные соотношения
Для определения токов и напряжений в электрической цепи по заданным параметрам источников и элементов составляется и решается система уравнений электрического равновесия. Эта система состоит из топологических и компонентных уравнений. Топологические – это уравнения, составленные по законам Кирхгофа для токов (первый закон Кирхгофа) для каждого из независимых узлов (уравнение баланса токов):
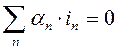 . (1.1)
. (1.1)
и напряжений (второй закон Кирхгофа) для каждого из независимых контуров (уравнение баланса напряжений):
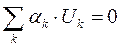 . (1.2)
. (1.2)
Здесь in(t) – ток n-й, ветви, взятый с плюсом ( 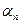 =1), если он втекает в узел, и с минусом – если вытекает(
=1), если он втекает в узел, и с минусом – если вытекает( 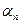 =-1). Это справедливо и для ветвей с источниками тока.
=-1). Это справедливо и для ветвей с источниками тока.
В ЗКН uk(t) – напряжение на k-й ветви, взятое с плюсом, если совпадают выбранные направления тока в ветви и обхода контура ( 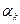 =1), в который эта ветвь входит. В противном случае uk(t) отрицательно, (
=1), в который эта ветвь входит. В противном случае uk(t) отрицательно, ( 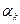 =-1). Для ветвей с источниками напряжения, напряжение источника входит в напряжение ветви со знаком минус, если стрелка внутри источника совпадает с условно выбранным направлением напряжения ветви, в противном случае – со знаком плюс. Что касается источников тока, то напряжение ветви на каждом из них можно выбирать произвольно. На идеальном источнике тока напряжение на нем находится на основании решения полной системы уравнений для данной цепи.
=-1). Для ветвей с источниками напряжения, напряжение источника входит в напряжение ветви со знаком минус, если стрелка внутри источника совпадает с условно выбранным направлением напряжения ветви, в противном случае – со знаком плюс. Что касается источников тока, то напряжение ветви на каждом из них можно выбирать произвольно. На идеальном источнике тока напряжение на нем находится на основании решения полной системы уравнений для данной цепи.
В топологии доказывается, что в электрической цепи, состоящей из q узлов и p ветвей независимых узлов Kну:
Kну= q-1-NE, (1.3)
а независимых контуров Kнк:
Kнк = p-q+1- NJ . (1.4),
Где: NE- число идеальных источников напряжения, которые не могут быть преобразованы в эквивалентные источники тока, NJ - число идеальных источников тока, которые не могут быть преобразованы в эквивалентные источники напряжения.
Это означает, что для не имеющей особенности цепи количество независимых уравнений, которое может быть составлено по первому закону Кирхгофа для токов равно q-1 , а по второму закону Кирхгофа для напряжений p-q+1.
Компонентные уравнения связывают токи и напряжения на идеальных пассивных элементах. Количество этих уравнений p-pит-pин, где pит и pин – количество ветвей с источниками тока и напряжения соответственно. Эти уравнения имеют следующий вид соответственно для сопротивления, емкости и индуктивности:
iR = uR/R; 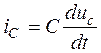 ;
; 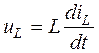 . (1.5)
. (1.5)
Для цепи, находящейся под гармоническим воздействием, составляется комплексная эквивалентная схема замещения, в которой мгновенные токи и напряжения представляются их комплексными амплитудами ( 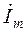 и
и 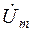 соответственно):
соответственно):
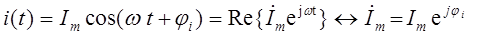 ,
,
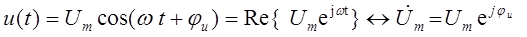 , (1.6)
, (1.6)
а пассивные элементы цепи – комплексными сопротивлениями в соответствии с соотношениями:
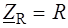 ,
, 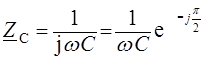 ;
; 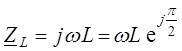 . (1.7)
. (1.7)
Связь между токами и напряжениями в них при этом определяется законом Ома в комплексной форме
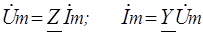 , (1.8)
, (1.8)
а законы Кирхгофа для токов и напряжений приобретают вид:
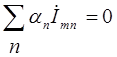 ,
, 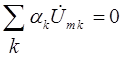 . (1.9)
. (1.9)
Таким образом, система уравнений электрического равновесия становится алгебраической, но комплексной.
Что касается мощностей, то комплексная мощность, потребляемая цепью определяется в виде
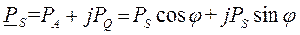 , (1.10)
, (1.10)
где 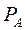 – активная мощность, характеризующая преобразование в цепи электрической в другие виды энергии,
– активная мощность, характеризующая преобразование в цепи электрической в другие виды энергии, 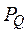 – реактивная мощность, характеризует процессы обмена энергией между цепью и источником,
– реактивная мощность, характеризует процессы обмена энергией между цепью и источником, 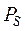 – полная мощность, потребляемая от источника.
– полная мощность, потребляемая от источника.
Приведенные соотношения используются при выполнении заданий 1 и 2 и подробно обсуждаются в [2,3].
Расчет сложных цепей при выполнении самотоятельной работы (задания 3, 4 и 5) выпоняется методами контурных токов, узловых напряжений (потенциалов), методом наложения и методом эквивалентного генератора.
Метод контурных токов (МКТ) основан на том, что токи всех ветвей могут быть выражены через токи главных ветвей (контурные токи). Каждый контурный ток проходит только по элементам своего контура. Количество контурных токов определяется количеством независимых контуров цепи (1.4). Количество же составляемых уравнений в МКТ может быть меньше (при наличии в цепи ветвей с вырожденными источниками тока уравнения для контуров в которые они входят не составляются, поскольку их контурные токи равны токам этих источников).
Уравнения МКТ в канонические форме записываются в виде:
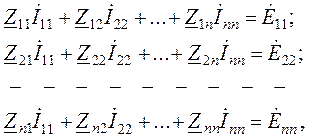 . (1.11)
. (1.11)
Здесь 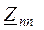 – собственное сопротивление n-го контура (всегда положительно), элементы
– собственное сопротивление n-го контура (всегда положительно), элементы 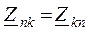 – взаимные сопротивления n-го и k-го контуров, взятые со знаком плюс при совпадении по направлению контурных токов в них. Контурная э.д.с.
– взаимные сопротивления n-го и k-го контуров, взятые со знаком плюс при совпадении по направлению контурных токов в них. Контурная э.д.с. 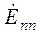 – алгебраическая сумма э.д.с. источников, входящих в контур (при совпадении с направлением контурного тока э.д.с. источника берется со знаком плюс).
– алгебраическая сумма э.д.с. источников, входящих в контур (при совпадении с направлением контурного тока э.д.с. источника берется со знаком плюс).
В методе узловых потенциалов (МУП) напряжения всех ветвей выражаются через разность потенциалов узлов, между которыми они включены. Количество узловых потенциалов определяется количеством независимых узлов цепи (1.3). Количество же составляемых в МУП уравнений может быть меньше (при наличии в цепи ветвей с вырожденными источниками напряжения уравнения для узлов к которым они подключены не составляются, поскольку их потенциалы равны напряжениям этих источников при подключении последних между данным узлом и базисным).
Уравнения МУП в канонические форме записываются в виде:
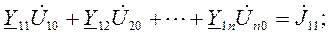
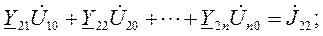 (1.12)
(1.12)
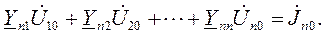
Здесь 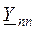 – собственная проводимость n-го узла (всегда положительна) сумма проводимостей ветвей подключенных к узлу, элементы
– собственная проводимость n-го узла (всегда положительна) сумма проводимостей ветвей подключенных к узлу, элементы 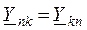 – взаимная проводимость n-го и k-го узлов – сумма проводимостей ветвей, соединяющих эти узлы взятая со знаком минус.
– взаимная проводимость n-го и k-го узлов – сумма проводимостей ветвей, соединяющих эти узлы взятая со знаком минус. 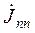 -алгебраическая сумма токов источников, подключенных к n-му узлу (втекающие с плюсом).
-алгебраическая сумма токов источников, подключенных к n-му узлу (втекающие с плюсом).
Метод наложенияиспользуется для нахождения тока или напряжения в одной из ветвей, если в линейной цепи несколько независимых источников энергии. Искомый ток 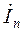 или напряжение
или напряжение 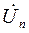 представляют суммой частичных токов
представляют суммой частичных токов 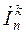 и соответственно напряжений
и соответственно напряжений 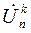 , каждый из которых найден из эквивалентной схемы, полученной последовательным выключением всех (кроме одного) независимых источников:
, каждый из которых найден из эквивалентной схемы, полученной последовательным выключением всех (кроме одного) независимых источников:
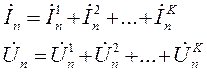 . (1.13)
. (1.13)
При выключении источников э.д.с. они закорачиваются, а источники тока – разрываются.
В методе эквивалентного генератора находится ток в одной из ветвей цепи. При этом, данная ветвь разрывается, а оставшаяся часть цепи представляется автономным двухполюсником – эквивалентным источником напряжения или тока. Параметрами эквивалентного источника напряжения являются напряжение и сопротивление холостого хода автономного двухполюсника. Параметрами эквивалентного источника тока являются ток короткого замыкания автономного двухполюсника и его входная проводимость. После этого, например в методе эквивалентного источника напряжения, ток ветви находится в соответствие с соотношением
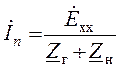 , (1.14)
, (1.14)
где 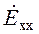 – напряжение холостого хода источника,
– напряжение холостого хода источника, 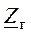 – его сопротивление,
– его сопротивление, 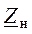 – сопротивление нагрузки источника (ветви, в которой определяется величина протекающего тока).
– сопротивление нагрузки источника (ветви, в которой определяется величина протекающего тока).
Далее приводятся варианты заданий для самостоятельного решения по этим темам. С примерами решения подобных задач можно ознакомиться в [4, 5].
Варианты заданий
| Вариант №1 | |||||
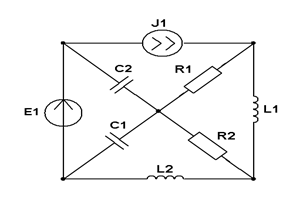 | Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. | ||||
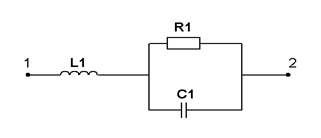 | R=1 кОм L=2 мГн C=0,5 нФ w=106 рад/с | ||||
| Определить комплексное сопротивление схемы Z экв и указать его характер (емкостной, индуктивный или резистивный) на заданной частоте. | |||||
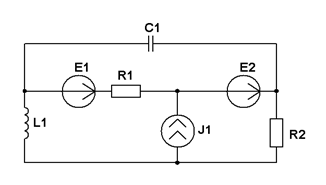
| Составить уравнения контурных токов и узловых напряжений и решить их для численных значений: R1=1 кОм; R2=100 Ом ; XL1=2 кОм; XC1=3 кОм; J1=1 мА; E1=25 В: E2=20 В; | ||||
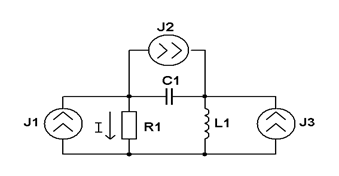 | R=1 кОм; XL=2 кОм; XC=3 кОм; J1=1 мА; J2=0,4 мА; J3=0,8 мА Рассчитать методом наложения ток в резисторе. | ||||
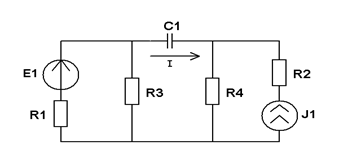 | E1=25 В: E2=20 В; R1=R2=R4=XC=100 Ом; R3=25 Ом. Методом эквивалентного генератора рассчитать ток в ветви с емкостью. |
| Вариант №2 | |||||
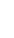  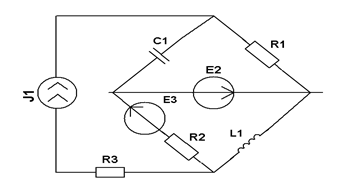
| Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. | ||||
 | R=2 кОм L=4 мГн C=0,4 нФ w=106 рад/с | ||||
| Определить мгновенное значение всех напряжений, если амплитуда напря-жения между точками 1 и 2 равна 1 В, а начальная фаза напряжения равна 0°. | |||||
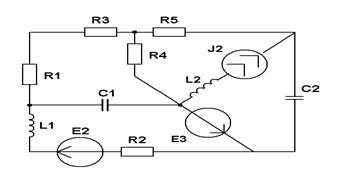
| Составить уравнения контурных токов и узловых напряжений и решить их для численных значений: R1=R2=R4= XC1=100 Ом R3=R5=XL1= XL2=25 Ом E2(t)=3coswt,В; E3(t)=5coswt, В.; J2(t)=0,4coswt, мА | ||||
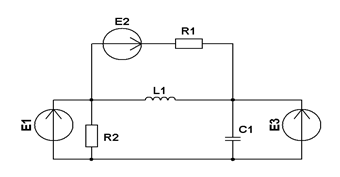 | R1=1 кОм; R3=2 кОм; XL=2 кОм; XC=3 кОм; e1=1 coswt, В; e2=3 coswt, В; e3=5 coswt, В. Рассчитать методом наложения ток в индуктивности. | ||||
| E=25 В; J=1 A; R1=R2=100 Ом; XL=25 Ом; XC=50 Ом. Методом эквивалентного генератора рассчитать ток в ветви с R1. | ||||
| Вариант №3 | |||||
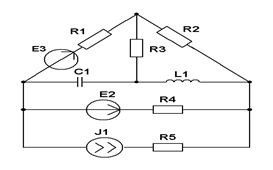
| Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. | ||||
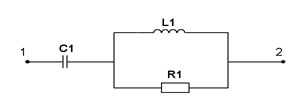 | R=3 кОм L=6 мГн C=0,3 нФ w=106 рад/с | ||||
| Определить мгновенное значение всех напряжений, если U1-2=1 В. | |||||
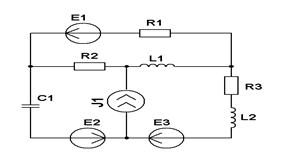
| Составить уравнения контурных токов и узловых напряжений и решить их для численных значений: R1=R2=R3= XC1=100 Ом XL1= XL2=25 Ом E1(t)=3coswt,В; J 1(t)=30coswt,мА; E2(t)=3coswt,В; E3(t)=5coswt, В.; | ||||
| Е1=80 В J=0,4 мА R1=R2=1 кОм XC=3 кОм XL=2 кОм. Рассчитать методом наложения ток в сопротивлении R2. | ||||
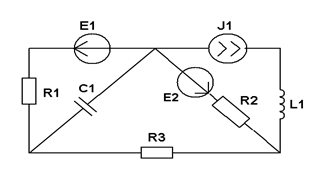 | 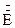 1=12 В 1=12 В 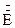 2=18 В 2=18 В 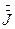 =1 A R1= XL =R2=12 Ом R3=XC=25 Ом Методом эквивалентного генератора рассчитать ток в ветви с R3. =1 A R1= XL =R2=12 Ом R3=XC=25 Ом Методом эквивалентного генератора рассчитать ток в ветви с R3. | ||||
| Вариант №4 | |||
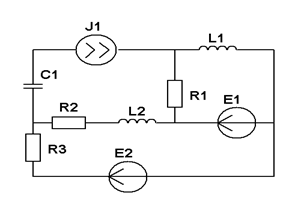
| Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. | ||
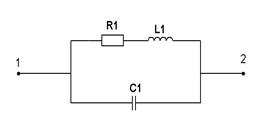 | R=4 кОм L=8 мГн C=0,1 нФ w=106 рад/с | ||
| Определить полную мощность, потребляемую цепью, если U1-2=1 В. | |||
напряжений и решить их для численных значений: R1=R2=R3= XC1=100 Ом; XL1= XL2=25 Ом; | |||
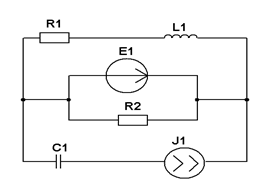
| R1=1 кОм; J1=0,4 мА; Е1 =1 В; XC1=3 кОм; XL1=2 кОм Рассчитать методом наложения ток в сопротивлении R1. | ||
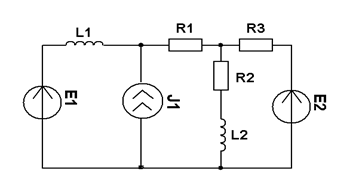 | E1=10 В; E2=20×еj90°; J=2×еj45° мA R1= 1 кОм R2=2 кОм R3=5 кОм XL1=4 кОм; XL2 =4 кОм Методом эквивалентного генератора рассчитать ток в ветви с R1. |
| Вариант №5 | |||
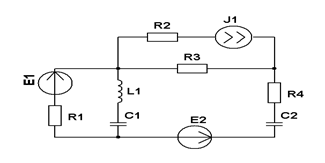
| Составить две системы уравнений электрического равновесия для мгновенных и комплексных значений электрических величин. | ||
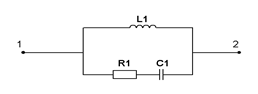
| R1=5 кОм; L1=10 мГн; C1=0,1 нФ; w=106 рад/с | ||
| Определить полную мощность, потребляемую цепью, если U1-2=1 В. | |||
Наши рекомендации
|
