Расчет цепи с реальной индуктивностью

Рассмотрим электрическую цепь, состоящую из источника питания и реальной катушки индуктивности (рис. 13а). L – индуктивность катушки, R – ее активное сопротивление. Эквивалентную схему реальной катушки называют индуктивным двухполюсником. Пусть по данной цепи проходит ток

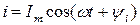(1)

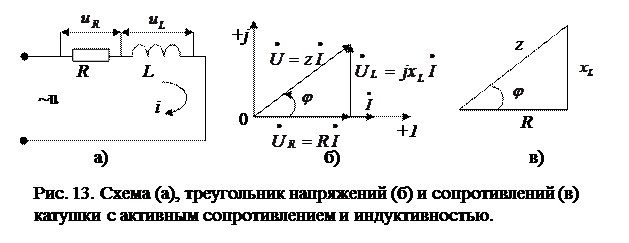Необходимо установить закон изменения напряжения на ее зажимах.

По второму закону Кирхгофа мгновенное значение напряжения равно сумме мгновенных значений напряжений на отдельных участках цепи:

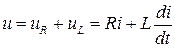(2)

Уравнение (2) называется уравнением баланса напряжений или уравнением электрического состояния индуктивности.

Так как данная цепь линейная, то каждое из напряжени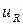й и 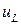является синусоидальным и имеет частоту, равную частоте тока 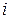. Поэтому подводимое напряжение 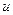тоже синусоидально:

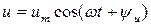(3)

Определим амплитуду 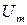и начальную фазу 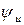напряжения 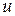, пользуясь комплексным методом. Перейдем от уравнения (2) для мгновенных значений напряжений к уравнению для комплексных действующих напряжений и тока:

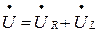(4)

Комплексное действующее значение тока равно: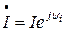

Комплексное действующее значение напряжений:

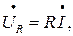
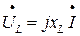(5)

Подставим значения (5) в (4) получим:

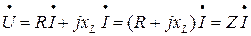(6)

Z - комплексное полное сопротивление:

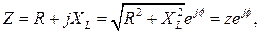(7)

где: 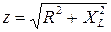- модуль комплексного полного сопротивления, 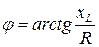- его аргумент.

Из выражения (6) получим закон Ома для индуктивного двухполюсника:

(8)

Подставим в (6) формулы для 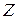и :

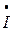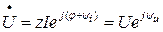(9)

Из (9) определим модуль напряжения и его начальную фазу:

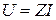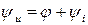, (10)

Начальная фаза 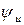положительна. Следовательно, подводимое напряжение опережает ток в цепи на угол .

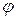На рис. 13б приведена векторная диаграмма реальной катушки. Для ее упрощения начальную фазу тока 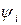приняли равной нулю, тогда вектор тока 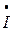совпадает с осью +1. Активное падение напряжения 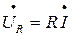совпадает по фазе с током, а вектор индуктивного падения напряжения 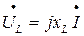опережает ток на угол 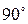. Векторную диаграмму рис. 13б называют треугольником напряжения.

Если каждую из сторон треугольника напряжений разделить на ток 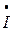, то получим треугольник сопротивлений (рис. 13в). Из него можно определить угол сдвига фаз между током и напряжением по формуле:

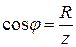(11)

Мгновенное значение мощности равно произведению мгновенных значений напряжений и тока:

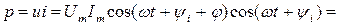
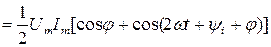
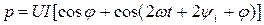(12)

На рис. 14 приведены графики напряжения, тока и мощности индуктивного двухполюсника.

Среднее значении мощности:

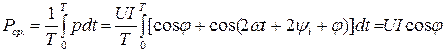
Учитывая, что 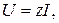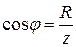, получим:

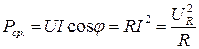(13)

Из полученного соотношения видно, что средняя мощность цепи равна ее активной мощности. Поэтому среднюю мощность обычно называют активной мощностью.

Наибольшее значение активной мощности называют полной мощностью и обозначают буквой S:

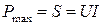. (14)

Величину 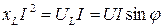называют реактивной индуктивной мощностью цепи, обозначают буквой

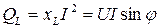. (15)

Активная, реактивная и полная мощности связаны между собой соотношением:

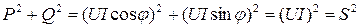
или

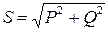(16)

Полную мощность принято измерять в вольтамперах (ВА).

Для пояснения каждой из этих мощностей рассмотрим графики на рис. 14. При 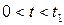, когда ток и напряжения положительны, мощность также положительна. Это означает, что в этот промежуток времени энергия источника расходуется на тепловую энергию и на энергию, запасаемую в магнитном поле . В течение времени 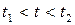мощность отрицательна. Это означает, что энергия частично возвращается обратно к источнику. В момент 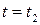к источнику возвратится энергия, равная заштрихованной площадке, ограниченной участком кривой и осью абсцисс.

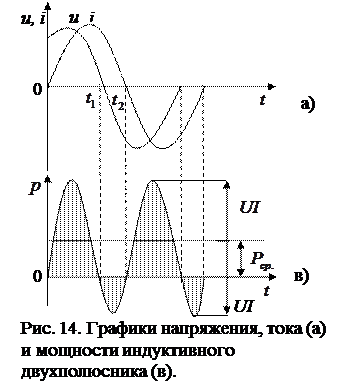Графически полная мощность S характеризует амплитуду колебания мощности около среднего значения. Полная мощность также является расчетной мощностью машины, т. к. она учитывает напряжение и ток, по величине которых выбираются все детали электротехнических устройств и аппаратов.