Определение начальных параметров внутренних усилий и деформаций при стесненном кручении тонкостенных стержней открытого профиля
Величина внутреннего усилия в сечении тонкостенного стержня определяется методом начальных параметров по табл. 6, где  – угол закручивания в начале координат;
– угол закручивания в начале координат;  – относительный угол закручивания в начале координат;
– относительный угол закручивания в начале координат;  – бимомент в начале координат;
– бимомент в начале координат;  – крутящий момент в начале координат. Начало координат располагается в левом сечении стержня.
– крутящий момент в начале координат. Начало координат располагается в левом сечении стержня.
Из четырех начальных параметров два неизвестных. Неизвестные начальные параметры определяются из условия крепления балки справа. Таким образом, при любом креплении однопролетной балки необходимо решать не более двух уравнений, вытекающих из условия опирания правого сечения балки (табл. 6).
Построение эпюр внутренних усилий
Аналитические выражения для определения внутренних усилий и деформаций можно составить по табл. 6. По результатам вычислений выполняется построение эпюр внутренних усилий:  или
или  – поперечных сил;
– поперечных сил; 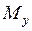 или
или  – изгибающих моментов;
– изгибающих моментов;  – бимомента;
– бимомента; 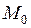 – момента чистого кручения;
– момента чистого кручения; 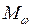 – изгибно-крутящего момента;
– изгибно-крутящего момента;  – внешнего крутящего момента.
– внешнего крутящего момента.
Вычисление нормальных напряжений
В сечениях тонкостенных стержней открытого профиля при стесненном кручении возникают нормальные напряжения
 ,
,
Таблица 6
Определение неизвестных начальных параметров
| № п/п | Схема закрепления балки | Начальные параметры |
 |     | |
 |     | |
 |      | |
 |      |
где N – продольная сила в сечении; 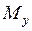 – изгибающий момент относительно оси Y;
– изгибающий момент относительно оси Y;  – изгибающий момент относительно оси X;
– изгибающий момент относительно оси X; 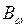 – изгибно-крутящий бимомент; А – площадь поперечного сечения;
– изгибно-крутящий бимомент; А – площадь поперечного сечения;
 – момент инерции относительно оси Х;
– момент инерции относительно оси Х;  – момент инерции относительно оси Y;
– момент инерции относительно оси Y; 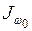 – секториальный момент инерции; Х, Y – эпюры линейных координат;
– секториальный момент инерции; Х, Y – эпюры линейных координат; 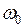 – эпюра главных секториальных координат.
– эпюра главных секториальных координат.
Вычисление касательных напряжений
Касательные напряжения при стесненном кручении тонкостенных стержней определяются выражением
 ,
,
где  – поперечная сила по направлению оси X;
– поперечная сила по направлению оси X;  – поперечная сила по направлению оси Y;
– поперечная сила по направлению оси Y; 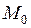 – момент при чистом кручении;
– момент при чистом кручении; 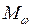 – изгибно-крутящий момент;
– изгибно-крутящий момент; 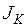 – момент инерции сечения при чистом кручении;
– момент инерции сечения при чистом кручении;  – секториальный момент инерции;
– секториальный момент инерции;  – эпюра статического момента отсеченной части сечения относительно оси Х;
– эпюра статического момента отсеченной части сечения относительно оси Х;  – эпюра статического момента отсеченной части сечения относительно оси Y;
– эпюра статического момента отсеченной части сечения относительно оси Y;  – площадь отсеченной части эпюры главных секториальных координат.
– площадь отсеченной части эпюры главных секториальных координат.
Для пояснения теории расчета тонкостенных стержней далее приведено несколько примеров.
ПРИМЕРЫ ВЫПОЛНЕНИЯ ЗАДАНИЯ
Пример №1
Исходные данные
Таблица 7
Исходные данные
| В, см | |
| Н, см | |
| δ, см | |
| q, кН/м | |
| L, м | |
| Е, ГПа | |
| G, ГПа |
В табл. 7 приведены исходные данные для примера №1. На рис. 5 и 6 даны поперечное сечение и расчетная схема рассматриваемого стержня.


