Виклад суті згаданого способу почнемо з визначника ІІ-го порядку
Отже, нехай дано
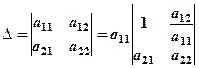 .
.
Домножимо елементи І-го рядка на 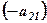 і почленно додамо до ІІ-го рядка.
і почленно додамо до ІІ-го рядка.
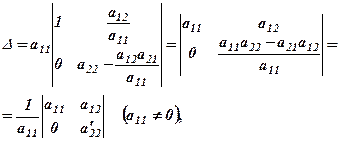
де 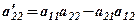 - знайдено за правилом прямокутника (див. 1.1). Таким чином, ми звели визначник до трикутної форми, і його значення дорівнює добутку діагональних елементів та коефіцієнта
- знайдено за правилом прямокутника (див. 1.1). Таким чином, ми звели визначник до трикутної форми, і його значення дорівнює добутку діагональних елементів та коефіцієнта 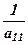 , тобто
, тобто
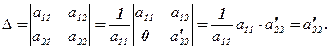 (1)
(1)
Застосуємо подібні перетворення для обчислення визначників ІІІ-го порядку
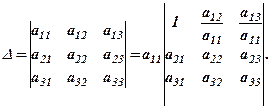
Згідно з властивістю визначників 8 домножимо елементи І-го рядка на 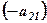 і додамо до відповідних елементів ІІ-го рядка. На місці елемента
і додамо до відповідних елементів ІІ-го рядка. На місці елемента  отримаємо
отримаємо 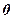 . Аналогічно, знову домножимо елементи І-го рядка на
. Аналогічно, знову домножимо елементи І-го рядка на 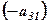 і додамо до відповідних елементів ІІІ-го рядка. На місці
і додамо до відповідних елементів ІІІ-го рядка. На місці  - теж
- теж 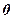 . Після цього співмножник
. Після цього співмножник 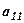 знову введемо в І-ий рядок, тоді
знову введемо в І-ий рядок, тоді
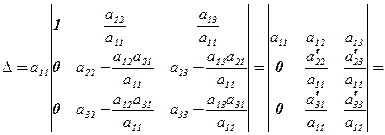
 (2)
(2)
де елементи 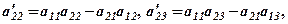
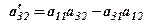 .
. 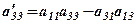 - знайдені за правилом прямокутника (див. 1.1).
- знайдені за правилом прямокутника (див. 1.1).
За співвідношенням (1) для мінора, що входить в останній визначник (2), маємо
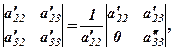
де 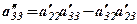 , при цьому вважається, що
, при цьому вважається, що 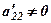 .
.
Отже, останній визначник із рівності (2) зводиться до трикутного вигляду, тобто в результаті маємо таку послідовність перетворень за правилом прямокутника
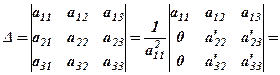
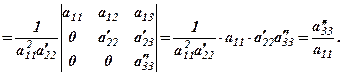 (3)
(3)
Для визначника 4-го порядку послідовність основних перетворень за правилом прямокутника має такий вигляд
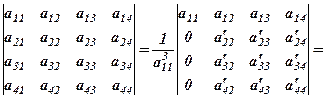

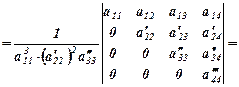
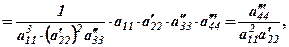 (4)
(4)

Очевидно, що при переході до визначника вищого порядку, наприклад, 5-го, ми можемо за правилом прямокутника і властивістю 8 утворити в першому стовпці, крім 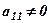 , нулі і звести задачу до обчислення визначника 4-го порядку.
, нулі і звести задачу до обчислення визначника 4-го порядку.
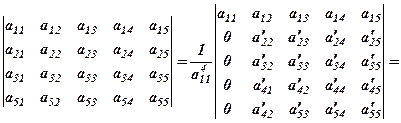

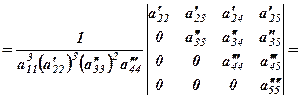
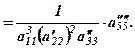 (5)
(5)
Тепер подамо алгоритм обчислення визначників за правилом прямокутника
1. Елемент 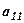 вважається провіднимі при цьому
вважається провіднимі при цьому 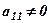 в супротивному випадку необхідно поміняти, із урахуванням знаку, стовпці або рядки місцями так, щоб елемент у першому рядку і першому стовпці був відмінним від нуля.
в супротивному випадку необхідно поміняти, із урахуванням знаку, стовпці або рядки місцями так, щоб елемент у першому рядку і першому стовпці був відмінним від нуля.
2. Перед визначником ставимо співмножник 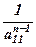 , де
, де 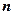 - порядок визначника, назвемо його поправочним коефіцієнтом. Значення показника степеня
- порядок визначника, назвемо його поправочним коефіцієнтом. Значення показника степеня 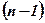 збігається з кількістю нулів, які будуть стояти в першому стовпці нижче елемента
збігається з кількістю нулів, які будуть стояти в першому стовпці нижче елемента 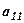 .
.
3. Елементи першого стовпця, що лежать нижче елемента 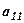 , заміняємо нулями, а всі інші – перетворюємо за правилом прямокутника, в буквеному вигляді вони позначені одним штрихом.
, заміняємо нулями, а всі інші – перетворюємо за правилом прямокутника, в буквеному вигляді вони позначені одним штрихом.
4. Наступним провідним елементом вибираємо по діагоналі 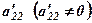 .
.
5. Вводимо в поправочний коефіцієнт співмножник 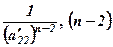 - кількість нулів, що будуть після
- кількість нулів, що будуть після 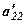 у другому стовпці.
у другому стовпці.
6. Замінюємо елементи ІІ-го стовпця, що лежать нижче 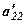 нулями, а всі інші - перетворюємо за правилом прямокутника, в буквеному вигляді вони позначаються двома штрихами.
нулями, а всі інші - перетворюємо за правилом прямокутника, в буквеному вигляді вони позначаються двома штрихами.
7. Процес перетворення продовжується поки не зведемо визначник до трикутної форми.
8. Знайдений добуток діагональних елементів скорочуємо з поправочними коефіцієнтами.
Зауваження. Описаний алгоритм у випадку дробових, або багатоцифрових елементів надійніше виконувати з застосуванням контролю, як це викладено в (1.1)
Приклад 1. Обчислити визначник: а) за алгоритмом; б) за допомогою обчислювальної таблиці з контролем.
а) 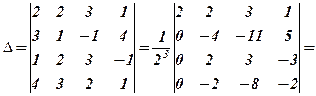
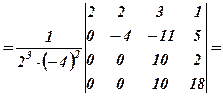
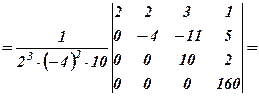
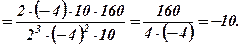
б) Обчислювальна таблиця
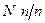 | 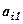 |  | 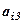 | 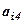 | Сума 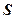 | Контроль |
| -1 | ||||||
| -1 | ||||||
| -4 | -11 | -10 | -10 | |||
| -3 | ||||||
| -2 | -8 | -2 | -12 | -12 | ||
