Гидростатический и пьезометрический напоры

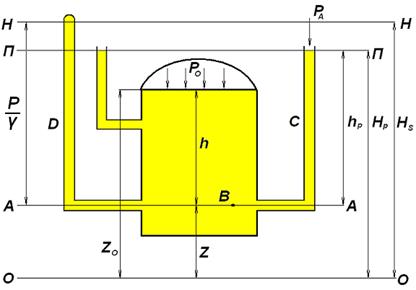Рассмотрим состояние равновесия жидкости, находящейся в закрытом резервуаре (рис. 2.12).

Рис. 2.12

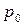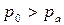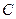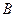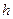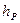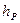Пусть давление воздействует на свободную поверхность жидкости и несколько превышает атмосферное, т.е. . Тогда, под влиянием избыточного давления со стороны резервуара жидкость в пьезометре , установленном в области произвольно выбранной точки на глубине , поднимется на высоту , где – пьезометрическая высота.

С целью сравнения положения различных точек в жидкости проведем горизонтальную плоскость сравнения 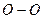. Вертикальное расстояние z от плоскости сравнения до какой-либо рассматриваемой точки называется геометрической высотой данной точки.

Пьезометрическим напором 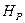жидкости, в какой – либо ее точке называется сумма геометрической высоты этой точки z и ее пьезометрической высоты 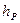, т.е.

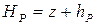. (2.52)

Значение пьезометрической высоты 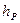может быть определено из условия равновесия жидкости в сосуде и пьезометре 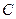, составленного относительно плоскости равного давлении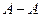

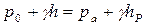. (2.53) Отсюда

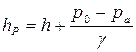, (2.54) следовательно, пьезометрический напор равен

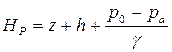. (2.55)

Для каждой точки жидкости сумма ее геометрической высоты z и глубины 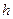выражает расстояние от плоскости сравнения 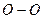до плоскости свободной поверхности жидкости, т.е. 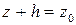. Поэтому

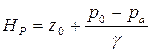. (2.56)

Так как правая часть равенства есть величина постоянная, не зависящая от местонахождения точек, то покоящаяся жидкость во всех своих точках обладает одинаковым пьезометрическим напором

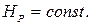(2.57)

Следовательно, если в различных точках резервуара установить не один, а несколько пьезометров, то уровни жидкости в них установятся в одной горизонтальной плоскости (например 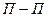) на высоте 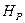от плоскости сравнения .

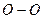Плоскость 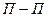, проведенная по уровням жидкости в пьезометрах, называется пьезометрической плоскостью или плоскостью пьезометрического напора.

Так как 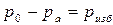, то можно сказать, что пьезометрический напор в какой-либо точке равен сумме ее геометрической высоты и высоты столба жидкости, соответствующего избыточному давлению в данной точке, т.е.

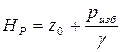. (2.58)

Гидростатическим напором жидкости 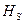в какой – либо ее точке называется сумма геометрической высоты этой точки и высоты столба жидкости, соответствующего абсолютному давлению жидкости в рассматриваемой точке, т.е.

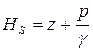. (2.59)

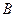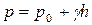Поскольку абсолютное давление в точке равно , то

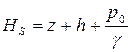, (2.60)

или

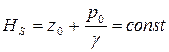. (2.61)

Следовательно, гидростатический напор жидкости во всех ее точках является величиной постоянной. Это положение также вытекает из сравнения выражений пьезометрического напора (2.56) и гидростатического напора (2.60), откуда следует, что гидростатический напор превышает величину пьезометрического напора на постоянную величину, равную высоте столба жидкости, соответствующего атмосферному давлению

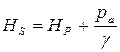. (2.62)

Высоту 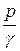, входящую в уравнение (2.59), геометрически можно представить как высоту поднятия жидкости в замкнутом пьезометре 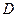, из которого выкачан воздух и устранено атмосферное давление, т.е. 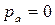. Благодаря этому, жидкость в пьезометре 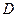поднимается на дополнительную высоту, соответствующую устраненному атмосферному давлению, равную .

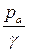Горизонтальная плоскость 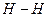, проведенная на высоте 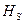от плоскости сравнения 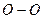и на высоте 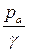от плоскости 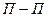, называется напорной плоскостью или плоскостью гидростатического напора.

Установив геометрическую сущность гидростатического и пьезометрического напора, выясним теперь их энергетический смысл. Для этого определим потенциальную энергию частицы жидкости весом 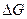, находящейся в области точки 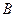. Под воздействием гидростатического давления 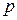эта частица по трубке пьезометра 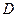поднимается на высоту равную 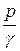и по отношению к плоскости сравнения 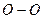окажется на высоте, равной 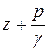, то есть на высоте гидростатического напора 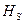. Полная потенциальная энергия данного количества жидкости относительно плоскости сравнения будет равна

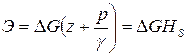. (2.63)

Определяем удельную энергию 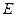рассматриваемого количества жидкости, т.е. энергию, отнесенную к единице веса жидкости

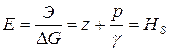. (2.64)

Таким образом, с энергетической стороны гидростатический напор представляет собой удельную энергию жидкости относительно выбранной плоскости сравнения 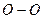. При этом составляющая 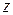выражает удельную потенциальную энергию положения, а составляющая 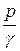– удельную потенциальную энергию абсолютного давления.

Рассуждая аналогичным образом, нетрудно показать, что пьезометрический напор представляет удельную потенциальную энергию, соответствующую избыточному давлению в рассматриваемой точке жидкости.

Так как покоящаяся жидкость во всех своих точках обладает одинаковым гидростатическим и одинаковым пьезометрическим напорами, то из всего рассмотренного также следует, что все частицы жидкости, находящиеся в состоянии покоя, обладают еще и одинаковой удельной энергией, т.е.

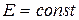. (2.65)