Наведемо приклад еквівалентних співвідношень

~ .

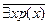Перевіримо істинність даного виразу. Нехай для деякого предиката “р” визначеного на множині М ліва частина істинна, тоді не існує аÎМ для якого р(х) істина, тоді р(х) – хибне. Тобто - істинне. Права частина співвідношення твердить, що для всіх хÎМ, - істинне. І права частина істинна. Тобто і ліва частина і права мають однакові істиностні значення.

Нехай ліва частина хибна. Тоді існує аÎМ, для якого р(х) – істинне, тоді твердження, що "х - є помилковим. Тобто права та ліва частина виразу еквівалентні.

Аналогічно доводиться, що 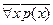~ (самостійно).

Дистрибутивність квантора загальності "х відносно кон’юнкції і квантора існування $х відносно диз’юнкції.

Доведемо дистрибутивність "х відносно кон’юнкції, тобто ~

Нехай ліва частина істинна. Тоді для довільного аÎМ є 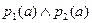, тому р₁(а) та р₂(а) істинні. Тому вираз - істинний.

Нехай ліва частина хибна. Тоді для деякого аÎМ або р₁(а) або р₂(а) – хибні. Тоді хибним є висловлення або "х р₁(х) або "р₂(х), а отже є хибним . Що і треба довести.