Неподвижные точки одномерного отображения

Изучим динамику популяции, т.е. вид последовательности при при различных значениях параметра l.

При небольших значение 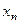стремится к нулю независимо от выбора x₁, т. е. популяция, численность которой мы рассматриваем, выжить не может, сколько бы бактерий не было вначале. Поведение последовательности удобно представить графически. Построим кривую при одном из рассматриваемых значений l и прямую у = х (см. рисунок). Отложим x₁ по оси абсцисс, проведём вертикаль до пересечения с кривой у = f (x) (точка А), затем горизонталь до пересечения с прямой у = х (точка В) и снова вертикаль до пересечения с кривой y = f (x) (точка С с координатой x₂). Легко проверить, что x₂ = f (x₁). Взяв точку x₂ за начальную и повторив те же операции, получим x₃, x₄ и т. д. Из рисунка видно, что при

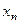Из формулы (14.2) следует, что функция f (x) переводит отрезок [0, 1] в отрезок [0, 1/4]. Если то все значения лежат на отрезке [0, 1] при условии, что Именно поэтому говорят, что формула (14.2) задаёт отображение отрезка на себя.

При значениях l, немного больших 1, последовательность стремится к некоторому постоянному значению 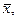зависящему от l. Следовательно, численность популяции с течением времени стабилизиру­ется (см. рисунок). Для модели (14.2) это означает, что, начиная с некоторого момента, будет выполняться равенство:

позволяющее определить значение 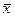из уравнения:

(14.3)

При l < 1 квадратное уравнение (14.3) имеет один неотрицательный корень При l > 1 квадратное уравнение (14.3) имеет два неотрицательных корня:

(14.4)

При l = 1 происходит бифуркация: в системе появляется устойчивая неподвижная точка 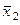, а точка 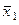теряет устойчивость.