Определение, особенности и общая характеристика оптимальных систем

ОПТИМАЛЬНЫЕ И АДАПТИВНЫЕ СИСТЕМЫ

(лекции, заочный факультет, 5 курс)

Лекция 1.

Введение.

В классической теории автоматического управления (ТАУ) за­дачи оптимизации и адаптации ставились в основном примени­тельно к управлению «в малом». Это означает, что оптимальная программа изменения режимов технологического процесса, вы­раженная в задающих воздействиях регуляторов, считалась из­вестной, определенной на стадии проектирования. Задача управ­ления заключалась в выполнении этой программы, стабилизации программного движения. При этом допускались лишь малые от­клонения от заданного движения, и переходные процессы «в ма­лом» оптимизировались по тем или иным критериям.

В конце 50-х - начале 60-х гг. XX столетия появились работы Л.С. Понтрягина (принцип максимума), Р. Беллмана (динамичес­кое программирование), Р. Калмана (оптимальная фильтрация, управляемость и наблюдаемость), которые заложили основы со­временной теории автоматического управления, общепринятого определения понятия которой пока не существует.

Наиболее точно современную теорию автоматического управ­ления можно отделить от классической ТАУ, учитывая требования научно-технического прогресса, современной и перспектив­ной автоматизации. Важнейшим из таких требований является оптимальное использование всех располагаемых ресурсов (энер­гетических, информационных, вычислительных) для достижения главной обобщенной конечной цели при соблюдении ограниче­ний.

Прежде всего указанная оптимиза­ция требует полного использования имеющейся априорной ин­формации в виде математической модели управляемого процес­са или объекта. Использование таких моделей не только на стадии проектирования, но и в процессе функционирования систем, яв­ляется одной из характерных черт современной теории автомати­ческого управления.

Оптимальное управление возможно лишь при оптимальной обработке информации. Поэтому теория оптимального (и субоп­тимального) оценивания (фильтрации) динамических процессов является составной частью современной теории автоматического управления. Особо важной является параметрическая идентифи­кация (оценивание параметров и характеристик по эксперимен­тальным данным), выполняемая в реальном масштабе времени в эксплуатационных режимах ОУ.

Подлинная оп­тимизация автоматического управления в условиях неполной априорной информации возможна только в процессе функциони­рования системы в текущей обстановке и возникшей ситуации. Следовательно, современная теория автоматического управления должна рассматривать адаптивное оптимальное (субоптимальное) управление «в большом». Кроме того, современная теория авто­матического управления должна рассматривать методы резерви­рования и структурного обеспечения надежности (особенно прин­ципы автоматической реконфигурации системы при отказах).

Определение, особенности и общая характеристика оптимальных систем.

Оптимальной называется наилучшая в некотором технико-эко­номическом смысле система. Основной ее особенностью являет­ся наличие двух целей управления, которые эти системы реша­ют автоматически.

Основная цель управления — поддержание управляемой ве­личины на заданном значении и устранение возникающих откло­нений этой величины.

Цель оптимизации - обеспечение наилучшего качества уп­равления, определяемое по достижению экстремума некоторого технико-экономического показателя, называемого критерием оптимальности (КО).

Оптимальные системы разделяют в зависимости от вида КО на два класса: оптимальные в статике системы и оптимальные в ди­намике системы.

У оптимальных в статике систем КО является функцией пара­метров или управляющих воздействий. Этот критерий имеет экст­ремум в статическом режиме работы системы, причем статическая характеристика, выражающая зависимость КО от управляющих воздействий оптимизации, может непредвиденным образом сме­щаться под действием возмущений. Оптимальная система должна этот экстремум находить и поддерживать. Такие системы приме­нимы, если возмущения, смещающие указанную характеристи­ку, изменяются сравнительно медленно по сравнению с длитель­ностью переходных процессов в системе. Тогда система будет успевать отслеживать экстремум практически в статическом ре­жиме. Такие условия обычно выполняются на верхней ступени иерархии управления.

Оптимальные в динамике системы отличаются тем, что их критерий оптимальности представляет собой функционал, т. е. функцию от функций времени. Это значит, что, задав функции времени, от которых данный функционал зависит, получим чис­ловое значение функционала. Эти системы могут применяться при сравнительно быстро меняющихся внешних воздействиях, не выходящих, однако, за допустимые пределы. Поэтому они ис­пользуются на нижних уровнях управления.

1.2. Критерии оптимальности оптимальных в динамике систем

Обычно эти функционалы имеют вид определенных интегра­лов по времени

где x(t), u(t) - векторы состояния и управления данной системы;

Т - длительность процесса (в частности, может быть Т = ).

В зависимости от подынтегральной функции f₀ эти критерии имеют следующие основные виды.

1. Линейные функционалы, у которых f₀ - линейная функция переменных:

- критерий максимального быстродействия при f₀ 1, т.е.

,

который равен длительности процесса, а соответствующие системы называют оптимальными по быстродействию;

- линейные интегральные оценки

- критерий максимальной производительности

,

где q(t) - количество произведенной продукции.

2. Квадратичные функционалы, у которых f₀ - квадратичная форма от входящих в нее переменных:

- квадратичные интегральные оценки качества переходного процесса

;

-критерий энергозатрат на управление, у которого

,

где u - управляющее воздействие, а и² - мощность, затрачи­ваемая на управление;

- обобщенный квадратичный критерий, равный сумме двух предшествующих, взятых с некоторыми весовыми коэффи­циентами. Он компромиссно характеризует качество пере­ходного процесса и энергозатраты на него, т. е.

,

где Q и R - положительно определенные квадратные матрицы. Функционалы, не содержащие интегралов:

- критерий минимакса, при оптимизации по которому надо обеспечить минимальное значение максимума модуля (нор­мы) вектора отклонения управляемого процесса от его эта­лонного закона изменения, т. е.

, где x_э – эталонный закон изменения.

Простейшим примером этого критерия для скалярного случая является известное максимальное перерегулирова­ние переходного процесса;

- функция от конечного состояния

,

которая является функционалом потому, что конечное со­стояние объекта х(Т) является функцией от управляющего воздействия u(t). Этот критерий оптимальности может применяться в сумме с одним из рассмотренных выше критериев, имеющих вид определенного интеграла.

Выбор того или иного критерия оптимальности для конкретного объекта или системы производится на основании соответствующего изучения работы объекта и предъявляемых к нему требований технико-экономического характера. Этот вопрос не может быть решен в рамках только теории автоматического управления. В зависимости от физического смысла критерия оптимальности его требуется либо минимизировать, либо максимизировать. В первом случае он выражает потери, во втором случае технико-экономическую выгоду. Формально, поменяв знак перед функционалом, можно задачу по максимизации свести к задаче по минимизации.

Лекция 2.

1.3. Краевые условия и ограничения
для оптимальных в динамике систем

Основная цель управления в таких системах обычно формулируется как задача перевода изображающей точки из некоторого начального состояния х(О) в некоторое конечное х(Т) состояние. Начальное состояние принято называть левым концом оптимальной траектории, а конечное - правым. Вместе взятые эти данные и образуют краевые условия. Задачи управления могут отличаться видом краевых условий.

1. Задача с закрепленными концами траектории имеет место, когда х(0) и х(Т) фиксированные точки пространства.

2. Задача с подвижными концами траектории получается, когда х(0) и х(Т) принадлежат некоторым известным линиям или поверхностям пространства.

3. Задача со свободными концами траектории возникает, когда указанные точки занимают произвольные положения. На практике встречаются и смешанные задачи, например х(0) - фиксирован, а х(Т) подвижен. Такая задача будет иметь место, если объект из заданного фиксированного состояния должен «догнать» некоторую эталонную траекторию (рис. 1).

Рис. 1.

Ограничениями называются дополнительные условия, кото­рым должны удовлетворять управляющие воздействия и управ­ляемые величины. Встречаются два вида ограничений.

1. Безусловные (естественные) ограничения, которые выпол­няются в силу физических законов для процессов в объекте уп­равления (ОУ). Эти ограничения показывают, что некоторые ве­личины и их функции не могут выйти за границы, определяемые равенствами или неравенствами. Например, уравнение двигате­ля постоянного тока (ДПТ):

,

ограничение на скорость асинхронного двигателя , где - синхронная скорость.

2. Условные (искусственные) ограничения, выражающие та­кие требования к величинам или функциям от них, согласно ко­торым они не должны превосходить границ, определенных равен­ствами или неравенствами по условиям долговечной и безопасной эксплуатации объектов. Например, ограничение на питающее напряжение 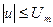, ограничения на допустимую скорость, уско­рение и т. п.

Для обеспечения условных ограничений необходимо прини­мать меры схемного или программного характера при реализации соответствующего управляющего устройства.

Ограничения, независимо от их вида, выражаемые равенства­ми, называются классическими, а неравенствами - неклассичес­кими.