Решение задач многомерной оптимизации

Задача, требующая нахождения оптимального значения функции m переменных Q(Х) = Q(x₁, x₂, …, x_m), называется задачей многомерной оптимизации. Так же, как и для случая одномерной оптимизации, задача нахождения максимума функции сводится к задаче нахождения минимума путем замены целевой функции Qна -Q.

В постановке задачи безусловной оптимизации для Q(Х)=Q(x₁,x₂,…,x_m) требуется найти хотя бы одну точку минимума Х* и вычислить Q*=f(Х*). Точка Х*Î R^m называется точкой глобального минимума функции Qна множестве Х, если для всех Х Î R^m выполняется неравенство Q(Х*) £ Q(Х). В этом случае значение Q(Х*) называется минимальным значением функции Qна R^m. Точка Х*ÎR^m называется точкой локального минимума функции Q, если существует такая d - окрестность U_dэтой точки (d>0), что для всех Х Î Х_d = Х U_d выполняется неравенство Q(X*) £ Q(X).

Для всякой непрерывно дифференцируемой функции Q достаточным условием того, что функция имеет точку минимума, является положительная определенность матрицы вторых частных производных (матрицы Гессе):

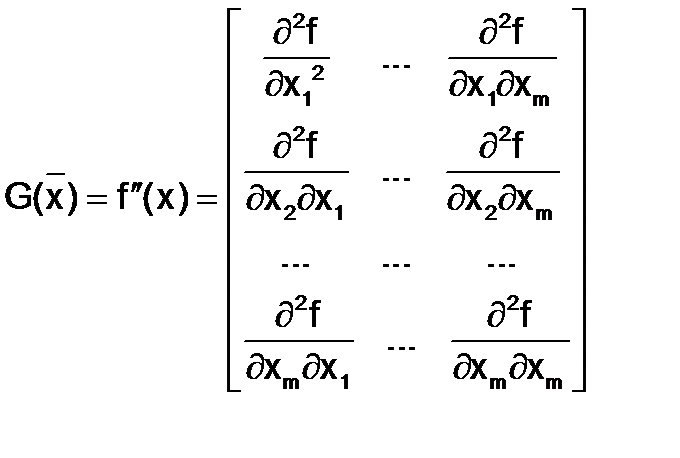
Известно, что для того чтобы матрица была положительно определена, необходимо, чтобы все угловые миноры были положительны. Так, для функции двух переменных Q(x, y) матрица Гессе имеет вид:

,

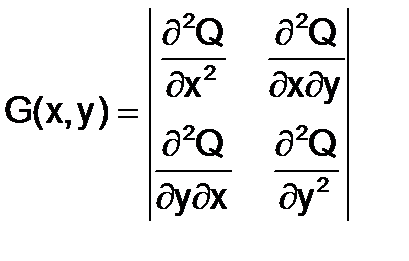а достаточным условием существования минимума является выполнение неравенств:

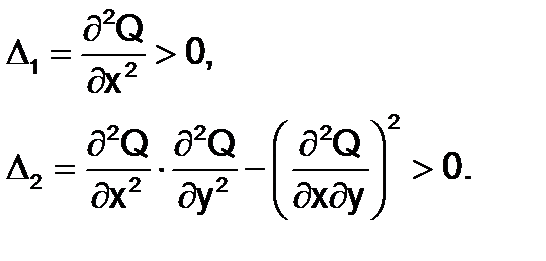
Аналитический метод поиска минимума применяется только для ограниченного круга задач. В основном это связано с необходимостью решения системы нелинейных уравнений, которая, как правило, решается численными методами. Гораздо проще решать задачу многомерной оптимизации численными методами, например, такими как метод градиентного спуска с дроблением шага и методы наискорейшего спуска с аналитическим или численным выбором шага[1].

Вычисление экстремума функции нескольких переменных

z = f(x₁, x₂, …x_n)

в MatLab осуществляет функция:

[X, Z] = fminsearch(name, x0),

где:

· name– имя функции, зависящее от n переменных;

· x0– вектор из n элементов, содержащий координаты точки начального приближения;

· X – вектор из n элементов, содержащий координаты точки, в которой достигается минимум;

· Z– значение функции в точке с координатами X.

Рассмотрим работу функции fminsearch()на примере определения минимума двумерной функции f(x1, x2) = x₁² + x₂² - x₂ - 2x₁ + 2.

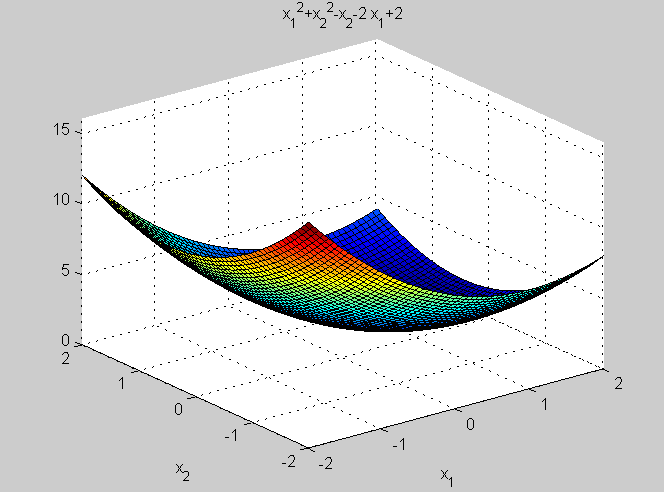
Рис. 2.6.1-1. Результат выполнения функции ezsurf()

Построим график (рис. 2.6.1-1) с использованием функции ezsurf(), аргументами которой служат: выражение функции, заключенное в одинарные кавычки, вектор изменения первой производной и вектор изменения второй переменной.

>> ezsurf ('x1.^2+x2.^2-x2-2*x1+2', [-2 2], [-2 2])

При нахождении минимума функции оформим многомерную функцию в виде m-функции (рис. 2.6.1-2).

Рис. 2.6.1-2. Целевая функция F(x)

Определим координаты точки минимума и значение функции в этой точке с использованием функции Matlab minsearch()(рис. 2.6.1-3).

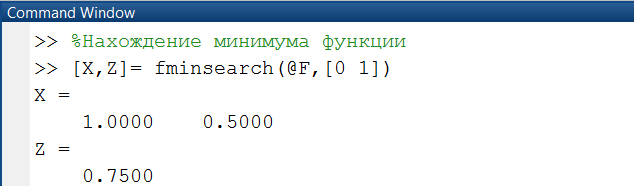Рис. 2.6.1-3. Использование функции fminsearch() для нахождения

минимума многомерной функции