Решение СЛАУ методом Гаусса
Обратная матрица
Матрица 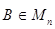 называется обратной к матрице
называется обратной к матрице 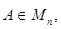 если AB = BA = Е; при этом пишут
если AB = BA = Е; при этом пишут 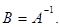 Матрица А имеет обратную только в том случае, если она невырожденная, то есть если
Матрица А имеет обратную только в том случае, если она невырожденная, то есть если 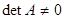 . Если
. Если 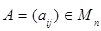 – невырожденная матрица, то
– невырожденная матрица, то
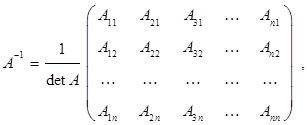
где 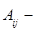 алгебраические дополнения элементов
алгебраические дополнения элементов 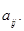
Системы линейных алгебраических уравнений
Системой линейных алгебраических уравнений (СЛАУ) называется система уравнений вида
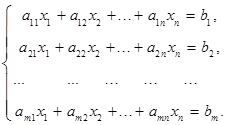
Система называется однородной, если свободные члены равны нулю: 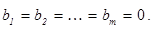 Однородная система всегда является совместной - она имеет решение
Однородная система всегда является совместной - она имеет решение 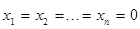 (возможно, не единственное).
(возможно, не единственное).
Матрицы
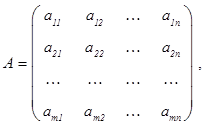
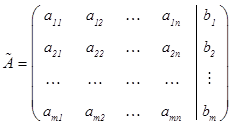 называются матрицей системы и расширенной матрицей системы соответственно; столбцы
называются матрицей системы и расширенной матрицей системы соответственно; столбцы 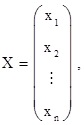
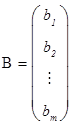 называются столбцом неизвестных и столбцом свободных членов соответственно. С учетом этих обозначений систему можно записать в матричной форме
называются столбцом неизвестных и столбцом свободных членов соответственно. С учетом этих обозначений систему можно записать в матричной форме 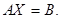
Решение СЛАУ с помощью обратной матрицы (матричный способ)
Система совместна при 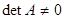 и имеет единственное решение – столбец
и имеет единственное решение – столбец 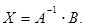
Задачи
Рассмотрим в аудитории типичные примеры, для решения которых используются приведенные определения, теоремы и понятия.
1.Найти обратную матрицу к матрице А и сделать проверку, если:
1) 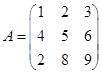 ;
;
Решение. Вычислим 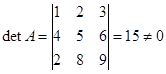 .
.
Матрица A невырожденная, следовательно, имеет обратную матрицу.
Найдем алгебраические дополнения ко всем элементам матрицы A:
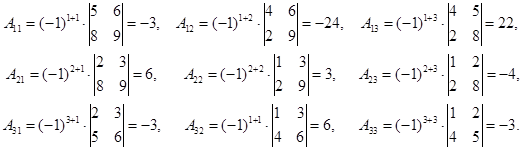
Тогда 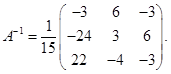
Проверка
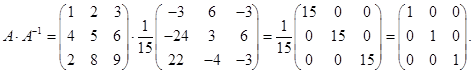
.
2) 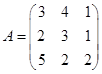 .
.
Ответ. 1) 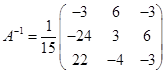 ; 2)
; 2) 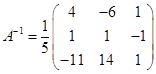 .
.
2.Решить СЛАУ матричным способом:
1) 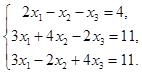
Решение. Пусть 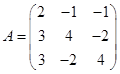 ,
, 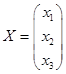 ,
, 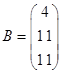 .
.
Тогда систему можно записать в матричном виде 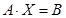 . Умножая последнее
. Умножая последнее
равенство на 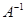 слева, получим:
слева, получим: 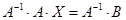 ,
, 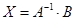 .
.
Найдем detA: 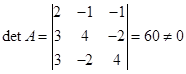 . Следовательно, существует обратная
. Следовательно, существует обратная
матрица 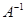 :
: 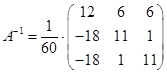 . Желательно сделать проверку:
. Желательно сделать проверку:
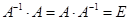 .
.
Отсюда 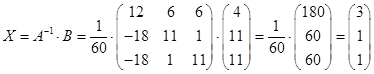 .
.
Имеем 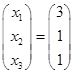 , т.е.
, т.е. 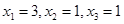 .
.
2) 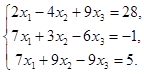
Ответ. 1) 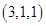 ; 2)
; 2) 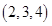 .
.
3.Даны 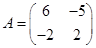 ,
, 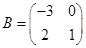 ,
, 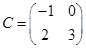 . Решить матричные уравнения:
. Решить матричные уравнения:
1) 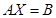 ; 2)
; 2) 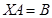 ; 3)
; 3) 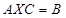 .
.
Решение. 1) 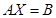 . Умножим слева на
. Умножим слева на 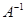 :
: 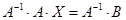 ,
, 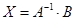 .
.
Найдем 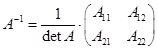 ,
, 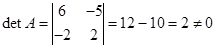 .
.
Матрица A невырожденная, т.е. имеет обратную матрицу.
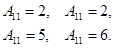
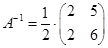 .
.
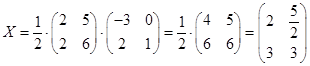 .
.
2) 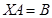 . Умножим справа на
. Умножим справа на 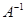 :
: 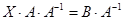 ,
, 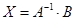 .
.
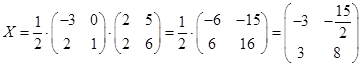 .
.
3) 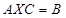 .
. 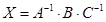 .
.
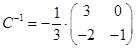 ;
;
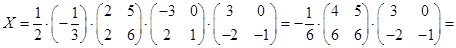
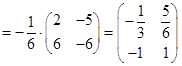 .
.
Ответ. 1) 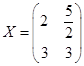 ; 2)
; 2) 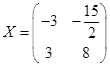 ; 3)
; 3) 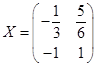 .
.
Задания для самостоятельного решения
1.Найти g(A), если:
1) 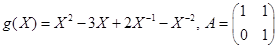 ;
;
2) 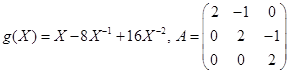 ;
;
3) 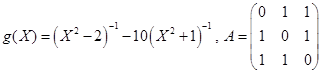 .
.
Ответ. 1) 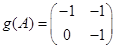 ; 2)
; 2) 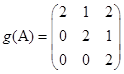 ; 3)
; 3) 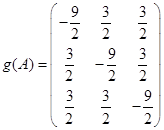 .
.
2.Решить матричные уравнения:
1) 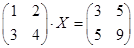 ; 2)
; 2) 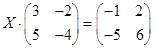 .
.
Ответ. 1) 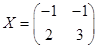 ; 2)
; 2) 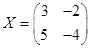 .
.
Правило Крамера
Обозначим
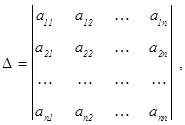
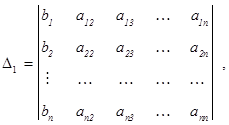
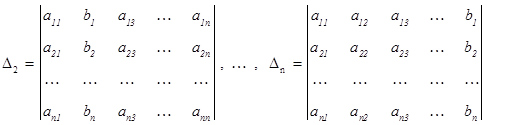
(определитель 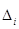 получается из D заменой i-го столбца на столбец свободных членов). Правило Крамера состоит в том, что при
получается из D заменой i-го столбца на столбец свободных членов). Правило Крамера состоит в том, что при 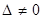 СЛАУ совместна и имеет единственное решение
СЛАУ совместна и имеет единственное решение 
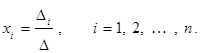
Решение СЛАУ методом Гаусса
При решении методом Гаусса расширенную матрицу 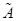 системы элементарными преобразованиями приводят к трапецеидальному виду. Затем, начиная с последнего уравнения, последовательно находят неизвестные.
системы элементарными преобразованиями приводят к трапецеидальному виду. Затем, начиная с последнего уравнения, последовательно находят неизвестные.
К числу элементарных преобразований относят:
1) перестановку столбцов или строк;
2) умножение столбца (строки) на число, отличное от нуля;
3) прибавление к столбцу (строке) другого столбца (другой строки), умноженного предварительно на некоторое число;
4) зачеркивание нулевого столбца (строки).
Трапецеидальной матрицей называется матрица 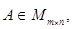 имеющая вид
имеющая вид
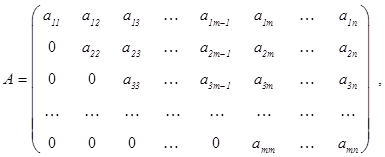
где 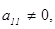
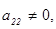
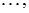
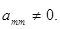
Задачи
Рассмотрим в аудитории типичные примеры, для решения которых используются приведенные определения, теоремы и понятия.
1.Решить систему по правилу Крамера:
1) 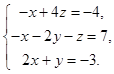
Решение. Находим главный определитель системы:
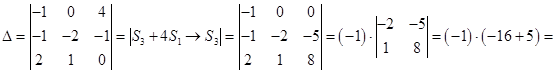
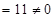 . Следовательно, система имеет единственное решение. Формулы Крамера:
. Следовательно, система имеет единственное решение. Формулы Крамера:
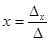 ,
, 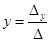 ,
, 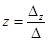 .
.
Вычислим определители 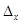 ,
, 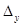 ,
, 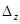 .
.
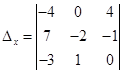 .
.
В главном определителе первый столбец заменили столбцом свободных членов.
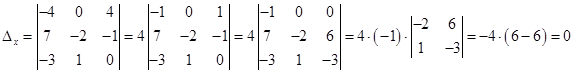 .
.
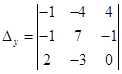 .
.
В главном определителе второй столбец заменили столбцом свободных членов.
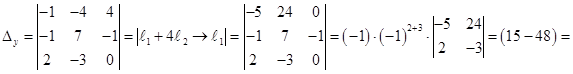
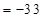 .
.
В главном определителе третий столбец заменим столбцом свободных членов.
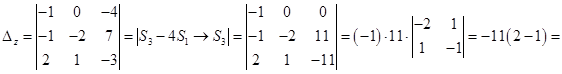
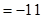 .
.
Находим 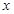 ,
, 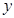 ,
, 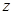 .
.
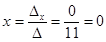 ;
; 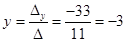 ;
; 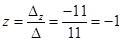 .
.
2) 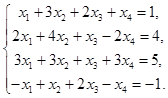
Ответ. 1) 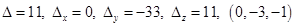 ;
;
2) 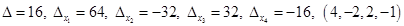 .
.
2.Решить СЛАУ методом Гаусса:
1) 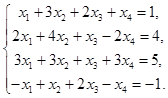
Запишем расширенную матрицу системы и выполним эквивалентные преобразования. В результате получим:
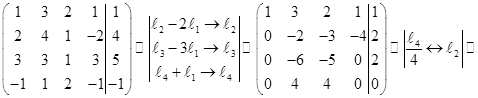
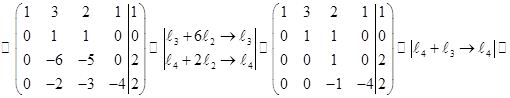
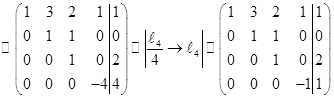 .
.
Последней матрице соответствует система линейных уравнений треугольного вида, т.е имеет единственное решение:

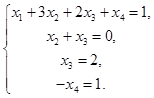 Получим решение системы:
Получим решение системы:
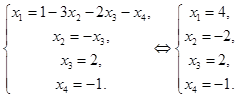
Метод последовательного исключения неизвестных предусматривает, что переменные можно исключать в любом порядке.
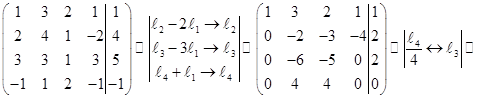
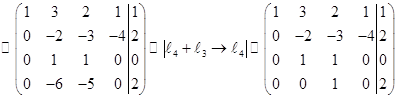 .
.
Последней матрице соответствует система линейных уравнений:
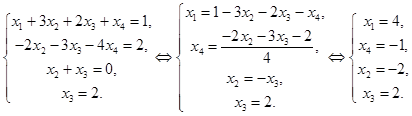
2) 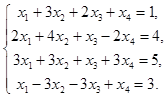
Запишем расширенную матрицу системы и выполним эквивалентные преобразования. В результате получим:
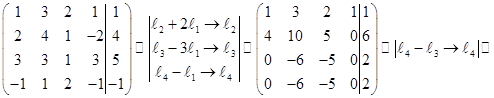
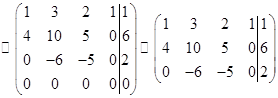 .
.
В последней матрице отбросили нулевую строку. Запишем систему линейных уравнений, соответствующую последней матрице:
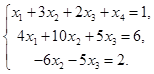
Эта система является совместной и неопределенной. Перенесем одно неизвестное, например 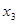 , в правую часть последнего уравнения системы, получим решение:
, в правую часть последнего уравнения системы, получим решение:
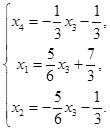
Неизвестному 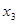 можно придать любые значения, поэтому система имеет бесчисленное множество решений.
можно придать любые значения, поэтому система имеет бесчисленное множество решений.
Рассуждая в терминах строчного ранга матрицы, можно заключить, что ранг матрицы системы равен 3 (число ненулевых строк после применения к ней метода Гаусса), а количество свободных неизвестных равно 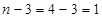 (n-число неизвестных системы).
(n-число неизвестных системы).
3) 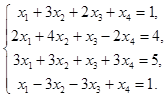
Выполнив над системой эквивалентные преобразования, получим:
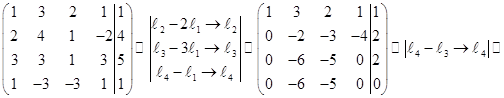
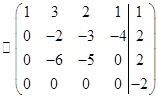 .
.
Получим систему:
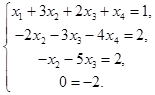
Получили противоречивый результат 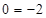 . Система несовместна (ранг расширенной матрицы, равный 4, оказался больше ранга матрицы системы, равный 3).
. Система несовместна (ранг расширенной матрицы, равный 4, оказался больше ранга матрицы системы, равный 3).
4) 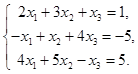 .
.
Ответ. 1) 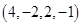 ; 2)
; 2) 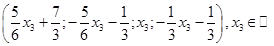 ;
;
3) Система несовместна; 4) 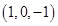 .
.
