Принципы организации методов одномерной минимизации
При решении задачи (5.4.1) некоторым итерационным методом, на итерации (5.4.2)
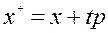 (5.6.1)
(5.6.1)
возникает необходимость минимизации одномерной функции 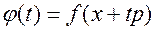 по параметру
по параметру 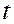 . Произвольный метод одномерной минимизации включает в себя этап нахождения отрезка локализации минимума и этап сокращения отрезка локализации.
. Произвольный метод одномерной минимизации включает в себя этап нахождения отрезка локализации минимума и этап сокращения отрезка локализации.
Этап локализации минимума опирается на следующий факт, справедливый для выпуклых функций:
Если
 (5.6.2)
(5.6.2)
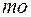
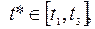
где  - точка минимума функции
- точка минимума функции 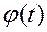 .
.
Локализация минимума производится посредством движения с нарастающим шагом в направлении убывания функции до тех пор, пока не прекратится убывание функции. При этом, если первый шаг привел к возрастанию функции, то производится смена направления на обратное и движение в обратном направлении. В результате всегда будет получена ситуация (5.6.2).
Этап сокращения отрезка опирается на факт:
если 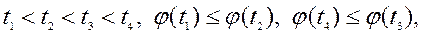 (5.6.3)
(5.6.3)
то на отрезке 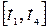 можно выделить отрезок локализации либо
можно выделить отрезок локализации либо 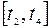 , если
, если  либо
либо 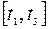 , если
, если 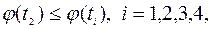 то есть сократить основной отрезок
то есть сократить основной отрезок 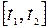 , отбрасывая один из крайних отрезков. После отбрасывания отрезка получим ситуацию (5.6.2). В ситуации (5.6.2) выбирается отрезок максимальной длины, внутри которого располагают новую точку, получая ситуацию (5.6.3). Продолжая процесс далее, можно получить сколь угодно малый отрезок локализации минимума. Подобным образом работают известные методы такие, как метод “золотого сечения” и метод на основе чисел Фибоначчи.
, отбрасывая один из крайних отрезков. После отбрасывания отрезка получим ситуацию (5.6.2). В ситуации (5.6.2) выбирается отрезок максимальной длины, внутри которого располагают новую точку, получая ситуацию (5.6.3). Продолжая процесс далее, можно получить сколь угодно малый отрезок локализации минимума. Подобным образом работают известные методы такие, как метод “золотого сечения” и метод на основе чисел Фибоначчи.
Отметим, что существует значительное множество методов одномерной минимизации, которые, с одной стороны используют идеи локализации и сокращения отрезка локализации на основании информации о значениях функции и градиента, а с другой – идеи полиномиальной аппроксимации минимизируемой функции на основании информации, получаемой в результате шагов спуска.
