Определение. Поверхностный интеграл называется потоком векторного поля через поверхность D

Если поверхность разбита на конечное число частичных поверхностей, то поток векторного поля через всю поверхность будет равен сумме потоков через частичные поверхности.

Если преобразовать скалярное произведение в координатную форму, то получаем соотношение:

Если на области D существует функция f(x, y, z), имеющая непрерывные частные производные, для которых выполняются свойства:

то такую функцию называют потенциальной функцией или потенциаломвектора .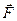

Тогда вектор 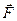является градиентом функции f.

Потенциал может быть найден по формуле:

В этой формуле x₀, y₀, z₀ – координаты некоторой начальной точки. В качестве такой точки удобно брать начало координат.

Теорема. Для того, чтобы поле вектора 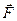, заданного в некоторой области, имело потенциал, необходимо и достаточно, чтобы выполнялось одно из двух условий:

1) Интеграл от вектора 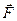по любому кусочно – гладкому контуру, принадлежащему области, равен нулю.

2) Интеграл по любому кусочно – гладкому пути, соединяющему две любые точки поля не зависит, от пути интегрирования.

Формула Стокса.

(Джордж Габриель Стокс (1819 – 1903) – английский математик)

Формула Стокса связывает криволинейные интегралы второго рода с поверхностными интегралами второго рода.

Пусть в пространстве задана некоторая поверхность S. L – непрерывный кусочно – гладкий контур поверхности S.

z S

L

y

D

l

x

Предположим, что функции P,Q и R непрерывны на поверхности S вместе со своими частными производными первого порядка. Применим формулу, выражающую криволинейный интеграл через определенный.

Введем обозначения:

Применив формулу Грина – Остроградского, можно заменить криволинейный интеграл равным ему двойным интегралом. После преобразований устанавливается следуюшее соответствие между криволинейным и поверхностным интегралом:

эта формула и называется формула Стокса.

Определение. Вектор , компоненты которого равны соответственно равны

называется вихремили ротором вектора и обозначается:

Определение. Символический вектор называется оператором Гамильтона.( Уильям Роуан Гамильтон (1805 – 1865) – ирландский математик) Символ Ñ - “набла”.

С учетом этого обозначения можно представить себе понятие ротора вектора 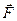как векторного произведения оператора Гамильтона на вектор .

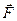Определение. Криволинейный интеграл, представляющий собой работу векторного поля вдоль некоторой кривой L называется линейным интеграломот вектора 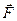по ориентированной кривой L.

Если кривая L представляет собой замкнутый контур, то линейный интеграл по такому контуру называется циркуляцией вектроного поля 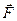вдоль контура L.

В векторной форме теорему Стокса можно сформулировать так:

Циркуляция вектора вдоль контура некоторой поверхности равна потоку вихря (ротора) через эту поверхность.

Отметим, что рассмотренная выше формула Грина – Остроградского является частным случаем формулы Стокса.

Также при условии равенства нулю всех компонент ротора вектора, получаем, что криволинейный интеграл по любой пространственной кривой равен нулю, т.е. криволинейный интеграл не зависит от пути интегрирования.

Определение. Выражение называется дивергенцией вектора (дивергенцией векторной функции) и обозначается

Таким образом, формулу Гаусса – Остроградского может быть записана в виде:

или

т.е. интеграл от дивергенции векторного поля 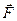по объему равен потоку вектора через поверхность, ограниченную этим объемом.

Определение. Векторное поле 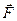называется соленоидальным (трубчатым), если div 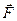=0 .

C помощью описанного выше оператора Гамильтона можно представить определенные нами понятия следующим образом:

Как было сказано выше (См. Уравнение Лапласа.), выражение

называется оператором Лапласа.

Справедливы следующие соотношения:

Справедливость этих равенств легко проверить непосредственной подстановкой.

Теперь рассмотрим примеры применения рассмотренных выше понятий.

Пример. Найти , если

Найдем скалярное произведение:

Найдем скалярное произведение:

Пример. Найти поток векторного поля через сторону треугольника S, вырезанного из плоскости координатными плоскостями.

z

x = 1 – z z = 1 - y

x

y = 1 - x

y

Пример. Найти div(grad u), если

Пример. Определить является ли векторное поле

и найти его потенциал.

Если поле потенциально, то должны выполняться следующие условия:

Эти условия эквивалентны условию равенства нулю ротора векторного поля.справедливость этого утверждения видна из формулы ротора.

Таким образом, поле потенциальное. Потенциал находится по формуле:

Содержание КВМ Часть 1.

Содержание КВМ Часть 2.

Содержание КВМ Часть 4.

Содержание:

Обыкновенные дифференциальные уравнения.

Основные определения.

Свойства общего решения.

Теорема Коши.

Интегральные кривые.

Особое решение.

Дифференциальные уравнения первого порядка.

Уравнения вида у’ = f(х).

Уравнения с разделяющимися переменными.

Однородные уравнения.

Уравнения, приводящиеся к однородным.

Линейные уравнения.

Линейные однородные дифференциальные уравнения.

Линейные неоднородные дифференциальные уравнения.

Метод Бернулли.

Метод Лагранжа.

Уравнение Бернулли.

Уравнения в полных дифференциалах.

Условие тотальности.

Уравнения вида у = f(y’) и x = f(y’).

Уравнения Лагранжа и Клеро.

Геометрическая интерпретация решений дифференциального

уравнения первого порядка.

Поле направлений.

Изоклины.

Численные методы решения дифференциальных уравнений.

Метод Эйлера.

Ломаная Эйлера.

Уточненный метод Эйлера.

Метод Рунге – Кутта.

Дифференциальные уравнения высших порядков.

Уравнения, допускающие понижение порядка.

Уравнения вида y⁽ⁿ⁾ = f(x).

Уравнения, не содержащие явно искомой функции и ее

производных до порядка n-1 включительно.

Уравнения, не содержащие явно независимой переменной.

Линейные дифференциальные уравнения высших порядков.

Линейные однородные дифференциальные уравнения

с произвольными коэффициентами.

Структура общего решения.

Фундаментальна система решений.

Определитель Вронского.

Общее решение линейного однородного дифференциального

уравнения второго порядка.

Линейные однородные дифференциальные уравнения с

постоянными коэффициентами.

Характеристический многочлен и характеристическое уравнение.

Линейные неоднородные дифференциальные уравнения с

произвольными коэффициентами.

Метод вариации произвольных постоянных.

Линейные неоднородные дифференциальные уравнения с

постоянными коэффициентами.

Уравнения с правой частью специального вида.

Нормальные системы обыкновенных дифференциальных

уравнений.

Нормальные системы линейных однородных

дифференциальных уравнений с постоянными коэффициентами.

Элементы теории устойчивости.

Устойчивость по Ляпунову.

Точка покоя.

Теорема Ляпунова.

Классификация точек покоя.

Уравнения математической физики.

Уравнения в частных производных.

Линейные однородные дифференциальные уравнения в

частных производных первого порядка.

Классификация основных типов уравнений математической физики.

Уравнение колебаний струны.

Граничные, начальные и краевые условия.

Решение задачи Коши методом разделения переменных. (Метод Фурье).

Решение задачи Коши методом Даламбера.

Уравнение теплопроводности.

Уравнение Лапласа.

Задача Дирихле.

Решение задачи Дирихле для круга.

Ряды.

Основные определения.

Свойства рядов.

Критерий Коши.

Ряды с неотрицательными членами.

Признак сравнения.

Признак Даламбера.

Предельный признак Даламбера.

Признак Коши.

Интегральный признак Коши.

Знакопеременные ряды.

Знакочередующиеся ряды.

Признак Лейбница.

Абсолютная и условная сходимость рядов.

Признак Даламбера и Коши для знакопеременных рядов.

Свойства абсолютно сходящихся рядов.

Функциональные последовательности.

Область сходимости.

Функциональные ряды.

Критерий Коши равномерной сходимости.

Признак Вейерштрасса.

Свойства равномерно сходящихся рядов.

Степенные ряды.

Теоремы Абеля.

Радиус сходимости.

Действия со степенными рядами.

Разложение функций в степенные ряды.

Решение дифференциальных уравнений с помощью степенных рядов.

Ряды Фурье.

Тригонометрический ряд.

Коэффициенты Фурье.

Достаточные признаки разложимости в ряд Фурье.

Разложение в ряд Фурье непериодической функции.

Ряд Фурье для четных и нечетных функций.

Ряд Фурье для функций любого периода.

Ряд Фурье по ортогональной системе функций.

Интеграл Фурье.

Преобразование Фурье.

Элементы теории функций комплексной переменной.

Свойства функций комплексной переменной.

Основные трансцендентные функции.

Производная функций комплексной переменной.

Условия Коши – Римана.

Интегрирование функций комплексного переменного.

Теорема Коши.

Интегральная формула Коши.

Ряды Тейлора и Лорана.

Изолированные особые точки.

Теорема о вычетах.

Вычисление интегралов с помощью вычетов.

Операционное исчисление.

Преобразование Лапласа.

Свойства изображений.

Таблица изображений некотрых функций.

Теорема свертки и запаздывания.

Интеграл Дюамеля.

Решение дифференциальных уравнений с помощью операционного

исчисления.

Криволинейные интегралы.

Криволинейные интегралы первого рода.

Свойства криволинейных интегралов первого рода.

Криволинейные интегралы второго рода.

Свойства криволинейных интегралов второго рода.

Формула Остроградского – Грина.

Поверхностные интегралы первого рода.

Свойства поверхностных интегралов первого рода.

Поверхностные интегралы второго рода.

Связь поверхностных интегралов первого и второго рода.

Формула Гаусса – Остроградского.

Элементы теории поля.

Поток векторного поля.

Потенциал.

Формула Стокса.

Ротор.

Оператор Гамильтона.

Циркуляция.

Дивиргенция.

Соленоидальное поле.

Ó Ларин Александр Александрович 2000 год. mailto: [email protected]