Погрешность измерительного преобразования

При измерительном преобразовании источником динамической погрешности является инерционность измерительного преобразователя. Значение динамической погрешности в этом случае будет зависеть не только от ДХ ИП, но и от формы входного сигнала. Оценка этой составляющей погрешности весьма сложна, поэтому ограничимся рассмотрением простейшего случая, когда ИП моделируется апериодическим звеном первого порядка. В этом случае дифференциальное уравнение ИП имеет вид

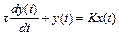, (4.36)

где 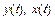- выходной и входной сигналы ИП;

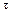- постоянная времени;

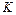- статический коэффициент преобразования.

Погрешность измерения 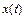, приведенная к максимальному значению входного сигнала 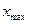будет равна

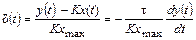. (4.37)

Так как скорость изменения выходного сигнала линейного инерционного ИП не может быть больше скорости изменения его входного сигнала, то максимальное значение 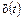можно найти из выражения

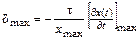. (4.38)

Для сигналов с финитным спектром известно неравенство Бернштейна, связывающее граничную частоту спектра 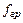с любой из его нормированных производных

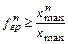. (4.39)

Для n = 1

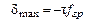. (4.40)

Отсюда можно получить допустимую инерционность ИП при измерительном преобразовании сигнала

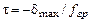. (4.41)

Так, для сигнала с граничной частотой спектра f_гр= 1 кГц и допустимой погрешностью d_max = 1% постоянная времени не должна превышать 10 ^–5 с.

Динамическая погрешность измерения с регистрацией
измеряемой величины во времени.

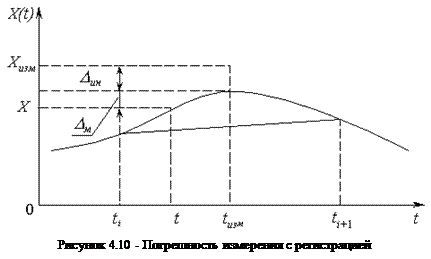
Измерение с регистрацией изменений величины во времени наиболее характерная задача динамических измерений, при решении которой осуществляются совместные измерения интересующей величины и времени. Наиболее часто эту задачу решают путем дискретизации измеряемой величины во времени с последующим восстановлением промежуточных значений с помощью различных интерполяционных функций (рис. 4.10).

В этом случае погрешность измерения имеет три составляющих

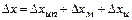. (4.42)

Здесь Dx_ип - инструментальная погрешность непосредственного измерения значения x(t) в точке t (имеет статическую и динамическую составляющую);

Dx_м - погрешность масштабирования появляющаяся из-за неточного измерения времени t ;

Dx_и – погрешность интерполяции, причиной которой является неточность восстановления x(t) по дискретным значениям.

Измеряемую величину представим в виде

x(t)=x f(t) (4.43)

где x - значениеx(t) в точке t;

f(t) - нормированная в точке t функция измеряемой величины.

Дифференцируя (4.43) по уровню и времени, получаем

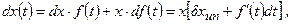
где 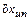- инструментальная относительная погрешность измерения;

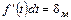- относительная погрешность масштабирования.

Последнюю составляющую можно представить в виде

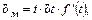(4.44)

где 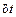- относительная погрешность измерения времени.

Из (4.44) видно, что погрешность масштабирования пропорциональна времени измерения, т.е. способна накапливаться во времени.

Для восстановления x(t) наиболее часто используют полином Лагранжа в общем случае степени n. В этом случае оценка 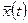измеряемой величины x(t) имеет вид

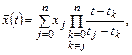(4.45)

где t – заданная временная координата на интервале интерполяции (t₀;t_n);

x_j ,t_j – координаты узлов интерполяции.

Оценка 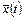отличается от 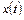на величину методической погрешности интерполяции 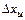, значение которой определяется остаточным членом полинома

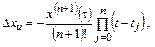(4.46)

где 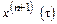- -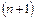я производная измеряемой величины в некоторой точке t интервала интерполяции. При малых погрешностях интерполяции можно считать, что 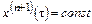во всем интервале .

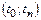Наиболее часто используют ступенчатую (n=0) и линейную (n=1) интерполяции.

В случае ступенчатой интерполяции (при n=0) 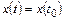, где 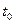- временная точка дискретизации, предшествующая t, а погрешность интерполяции

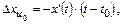(4.47)

Для линейной интерполяции (при n=1)

;

.

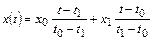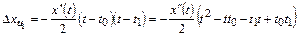Определим максимальное значение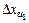

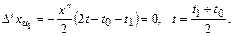
Отсюда

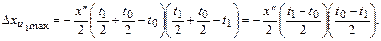
Для равномерной дискретизации

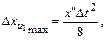(4.48)

где 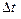- интервал дискретизации.