Бақылауға арналған сұрақтар және тапсырмалар
1. Қандай процестер толқындық теңдеуімен сипатталады?
2. Қандай процестер жылуөткізгіштік теңдеуімен сипатталады?
3. Қандай процестер Лаплас және Пуассон теңдеулерімен сипатталады?
4. Толқындық теңдеуді қорытып шығару керек.
5. Жылуөткізгіштік теңдеуді қорытып шығару керек.
6. Қосымша шарттар деген не? Бастапқы, шекаралық шарттар деген не?
7. Үш түрлі шекаралық шарттарды келтіріңіздер.
8. Гиперболалық және параболалық типті теңдеулерге қойылатын есептердің бастапқы шарттарының айырмашылығы қандай?
9. Бүйір беті жылу өткізбейтін 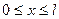 стерженьнің бір жақ
стерженьнің бір жақ 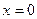 ұшы жылу өткізбейді, ал екінші
ұшы жылу өткізбейді, ал екінші 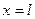 ұшына сырттан тұрақты жылу ағыны Q беріледі. Бастапқы температурасы нөлге тең деп алып, стерженьнің температурасын табуға байланысты есепті құру керек.
ұшына сырттан тұрақты жылу ағыны Q беріледі. Бастапқы температурасы нөлге тең деп алып, стерженьнің температурасын табуға байланысты есепті құру керек.
10. Ұзындығы 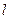 біртекті ішек
біртекті ішек 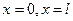 нүктелерінің арасында керілген.
нүктелерінің арасында керілген. 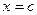 нүктесінде ішек тепе-теңдік қалыптан кішкене
нүктесінде ішек тепе-теңдік қалыптан кішкене 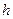 қашықтыққа созылып,
қашықтыққа созылып, 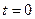 уақыт моментінде бастапқы жылдамдықсыз босатып жіберілген. Ішектің кез келген
уақыт моментінде бастапқы жылдамдықсыз босатып жіберілген. Ішектің кез келген 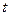 уақыт моментіндегі
уақыт моментіндегі 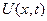 ауытқуын анықтау керек.
ауытқуын анықтау керек.
11. Центрі координаттардың басында орналасқан радиусы 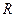 біртекті
біртекті 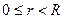 шардың бастапқы температурасы Т болсын. Беттің температурасы нольге тең өзгермейді деп ұйғарып, шардың температурасын табуға байланысты есепті құру керек.
шардың бастапқы температурасы Т болсын. Беттің температурасы нольге тең өзгермейді деп ұйғарып, шардың температурасын табуға байланысты есепті құру керек.
ТАРАУ
ШЕКАРАЛЫҚ ЕСЕПТЕР
6.1. Стационар емес теңдеулер үшін шекаралық есептер.Бастапқы және шектік шарттардың жиынын шекаралық шарттар деп атайды. Дифференциалдық теңдеулер шекаралық шарттармен бірге шекаралық есептер құрайды. Шекаралық есептерді шешу деп дифференциалдық теңдеудің берілген шекаралық шарттарды қанағаттандыратын шешімін табуды айтады. Шекаралық шарттың ішінде бастапқы мен шектік шарттардың екеуі де болуы міндетті емес. Егер шекаралық шарт тек бастапқы шарттардан тұратын болса, мұндай шекаралық шартқа сәйкес келетін есепті Коши есебі деп атайды.
Толқындық теңдеу үшін Коши есебі:
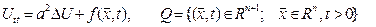 (6.1.1)
(6.1.1)
теңдеуін
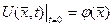 ,
, 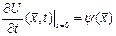 ,
, 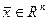 (6.1.2)
(6.1.2)
бастапқы шарттарын қанағаттандыратын 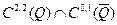 класына жататын
класына жататын 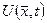 функциясын табуды толқындық теңдеуіне қойылған Коши есебі деп атайды. Мұндағы
функциясын табуды толқындық теңдеуіне қойылған Коши есебі деп атайды. Мұндағы 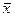 -
- 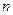 координатадан тұратын вектор, ал
координатадан тұратын вектор, ал 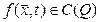 ,
, 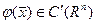 ,
, 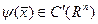 көрсетілген кеңістіктерде жататын белгілі функциялар.
көрсетілген кеңістіктерде жататын белгілі функциялар.
Жылуөткізгіштік теңдеуі үшін Коши есебі:
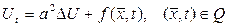 (6.1.3)
(6.1.3)
теңдеуін
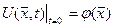 ,
, 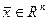 (6.1.4)
(6.1.4)
бастапқы шартын қанағаттандыратын 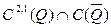 класында жататын
класында жататын 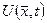 функциясын табуды жылуөткізгіштік теңдеуіне қойылған Коши есебі деп атайды. Мұндағы
функциясын табуды жылуөткізгіштік теңдеуіне қойылған Коши есебі деп атайды. Мұндағы 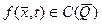 ,
, 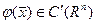 белгілі функциялар.
белгілі функциялар.
Екінші ретті дифференциалдық теңдеулер үшін жалпыланған Коши есебі:
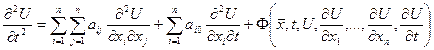 (6.1.5)
(6.1.5)
екінші ретті дифференциалдық теңдеу және бөлік–тегіс 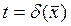 теңдеуімен анықталатын
теңдеуімен анықталатын 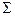 беті берсін. Q –деп
беті берсін. Q –деп 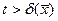 теңсіздігімен анықталатын және
теңсіздігімен анықталатын және 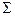 бетімен шенелген облысты белгілейік. (6.1.5) теңдеуін және
бетімен шенелген облысты белгілейік. (6.1.5) теңдеуін және
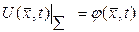 ,
, 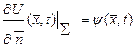 ,
, 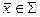 (6.1.6)
(6.1.6)
шекаралық шарттарын қанағаттандыратын 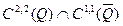 класына жататын
класына жататын 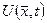 функциясын табу екінші ретті теңдеуге қойылған жалпыланған Коши есебі деп аталады. Мұндағы
функциясын табу екінші ретті теңдеуге қойылған жалпыланған Коши есебі деп аталады. Мұндағы 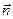 -
- 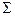 бетіне
бетіне 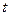 аргументінің өсу бағытына қарай бағытталған нормаль вектор.
аргументінің өсу бағытына қарай бағытталған нормаль вектор.
Енді шекаралық шартқа бастапқы да, шектік те шарттар қатысатын болсын. Мұндай шекаралық есептерді бастапқы– шекаралық есептер деп атайды. Олар есепке қатысатын шекаралық шарттардың түріне байланысты бастапқы – бірінші шекаралық, бастапқы - екінші шекаралық және бастапқы – үшінші шекаралық болып үш класқа бөлінеді. Мысалы, жылуөткізгіштік теңдеуі үшін қойылатын бастапқы - бірінші шекаралық есеп бір бастапқы шартты және бірінші шекаралық шарттарды қамтиды. Толқындық теңдеу үшін қойылатын бастапқы–бірінші шекаралық есеп екі бастапқы және бірінші шекаралық шарттарды қамтиды.
Жылуөткізгіштік теңдеуі үшін бастапқы –бірінші шекаралық есеп: Rn кеңістігінде жататын шенелген D облысын қарастырамыз. 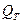 деп
деп 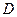 облысымен (0,Т] жартылай кесіндісінің бірігуінен шыққан цилиндрді белгілейік, яғни
облысымен (0,Т] жартылай кесіндісінің бірігуінен шыққан цилиндрді белгілейік, яғни
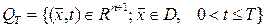 .
.
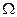 - деп
- деп 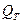 цилиндрінің бүйір бетін, яғни
цилиндрінің бүйір бетін, яғни
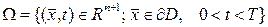
жиынын, ал
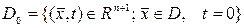
- деп QT цилиндрінің табанын белгілейік.
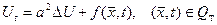 (6.1.7)
(6.1.7)
теңдеуін
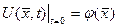 ,
, 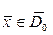 (6.1.8)
(6.1.8)
бастапқы шартын,
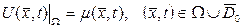 (6.1.9)
(6.1.9)
шекаралық шартын қанағаттандыратын 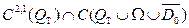 класына жататын U(x,t) функциясын табуды жылуөткізгіштік теңдеуіне қойылған бастапқы-бірінші шекаралық есеп деп атайды. Мұндағы
класына жататын U(x,t) функциясын табуды жылуөткізгіштік теңдеуіне қойылған бастапқы-бірінші шекаралық есеп деп атайды. Мұндағы 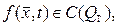
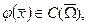
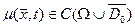 және
және 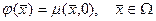 көрсетілген кеңістіктерде жататын белгілі функциялар.
көрсетілген кеңістіктерде жататын белгілі функциялар.
Жоғарыда келтірілген бастапқ–бірінші шекаралық есептің мағынасын, онда келтірілген белгілеулерді толық түсіндіру үшін бір өлшемді жылуөткізгіштік теңдеуіне қойылатын бастапқы –бірінші шекаралық есепке тоқталып өтейік, мұнда
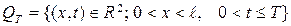
жартылай ашық тік төртбұрышты, 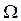 -осы тік төртбұрыштың QT жиынында жатпайтын бүйір қабырғаларында жататын нүктелерден тұратын жиынды,
-осы тік төртбұрыштың QT жиынында жатпайтын бүйір қабырғаларында жататын нүктелерден тұратын жиынды, 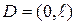 интервалын,
интервалын, 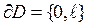 жиынын, ал
жиынын, ал 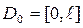 кесіндісін білдіреді (20 – сурет).
кесіндісін білдіреді (20 – сурет).
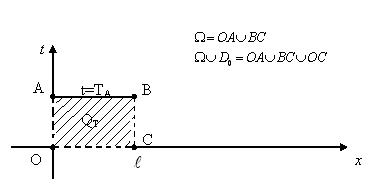
20 – сурет
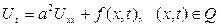
теңдеуін
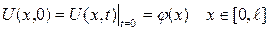
бастапқы шартын
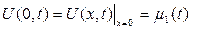
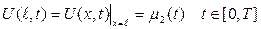
шекаралық шарттарын қанағаттандыратын 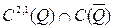 класында жататын U(x,t) функциясын табуды бір өлшемді жылуөткізгіштік теңдеуіне қойылған бастапқы-бірінші шекаралық есеп деп атайды. Мұндағы
класында жататын U(x,t) функциясын табуды бір өлшемді жылуөткізгіштік теңдеуіне қойылған бастапқы-бірінші шекаралық есеп деп атайды. Мұндағы 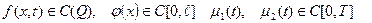 және
және 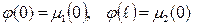 -
-
осы көрсетілген шарттарды қанағаттандыратын белгілі функциялар.
Толқындық теңдеуге қойылатын бастапқы –бірінші шекаралық есеп:
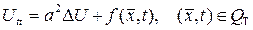
теңдеуін
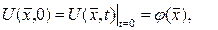
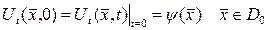
бастапқы шарттарын 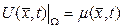 шекаралық шартын қанағаттардыратын
шекаралық шартын қанағаттардыратын 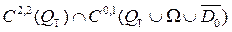 класында жататын
класында жататын 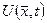 функциясын табуды толқындық теңдеуі үшін қойылған бастапқы–бірінші шекаралық есеп деп атайды.
функциясын табуды толқындық теңдеуі үшін қойылған бастапқы–бірінші шекаралық есеп деп атайды.
6.1.1 - ескерту. 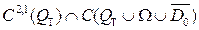 класында жататын жылуөткізгіштік теңдеудің,
класында жататын жылуөткізгіштік теңдеудің, 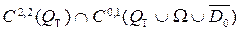 класында жататын толқындық теңдеуінің шешімдерін олардың классикалық шешімдері деп атайды.
класында жататын толқындық теңдеуінің шешімдерін олардың классикалық шешімдері деп атайды.
Жылуөткізгіштік және толқындық теңдеулері үшін бастапқы-екінші, бастапқы-үшінші шекаралық есептер жоғарыда қарастырылған бастапқы-бірінші шекаралық есептер сияқты қойылады. Олар сәйкесінше екінші және үшінші шекаралық шарттарды қамтиды. Мысалы, егер радиусы R - ге тең біртекті шардың шекарасы, температурасы 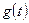 - ға тең сұйықпен жуылатын болса, және шардың шекарасындағы жылу алмасу Ньютон заңы бойынша жүрсе, онда осы процеске сәйкес келетін шекаралық есеп
- ға тең сұйықпен жуылатын болса, және шардың шекарасындағы жылу алмасу Ньютон заңы бойынша жүрсе, онда осы процеске сәйкес келетін шекаралық есеп
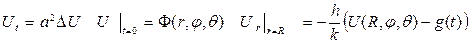
түрінде беріледі. Мұндағы 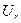 шамасы r бағытымен бағыттас нормаль бағытында алынған
шамасы r бағытымен бағыттас нормаль бағытында алынған 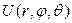 функциясының туындысы.
функциясының туындысы.
6.2. Стационар теңдеулер үшін шекаралық есептер 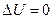 - Лаплас теңдеуі стационар процеске сәйкес келетін теңдеулердің бірі. Бұл жағдайда Лаплас теңдеуінің шешіміне бастапқы шарттың әсері болмайды. Сондықтан шекаралық шарттарда тек шектік шарттар ғана қатысады. Демек, Лаплас теңдеуі үшін үш түрлі шекаралық есеп қарастыруға болады.
- Лаплас теңдеуі стационар процеске сәйкес келетін теңдеулердің бірі. Бұл жағдайда Лаплас теңдеуінің шешіміне бастапқы шарттың әсері болмайды. Сондықтан шекаралық шарттарда тек шектік шарттар ғана қатысады. Демек, Лаплас теңдеуі үшін үш түрлі шекаралық есеп қарастыруға болады.
Кеңістікте тұйықталған 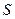 беті берілсін.
беті берілсін. 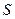 –беті кеңістікті екі облысқа бөледі.
–беті кеңістікті екі облысқа бөледі. 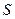 -беттің ішінде орналасқан облысты V+ - деп белгілейік. Демек, V+ облысы шенелген, ал
-беттің ішінде орналасқан облысты V+ - деп белгілейік. Демек, V+ облысы шенелген, ал 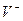 облысы шенелмеген болады. Енді осы облыстарда анықталған Лаплас теңдеуіне қойылатын шекаралық есептерге тоқталайық.
облысы шенелмеген болады. Енді осы облыстарда анықталған Лаплас теңдеуіне қойылатын шекаралық есептерге тоқталайық.
V+ облысында, яғни шенелген облыста берілген Лаплас теңдеуіне қойылатын шекаралық есептер:
1)
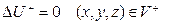
теңдеуін
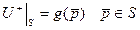
шекаралық шартын қанағаттандыратын 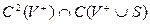 класында жататын
класында жататын 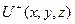 функциясын табуды Лаплас теңдеуіне қойылатын бірінші шекаралық есеп немесе ішкі Дирихле есебі деп атайды.
функциясын табуды Лаплас теңдеуіне қойылатын бірінші шекаралық есеп немесе ішкі Дирихле есебі деп атайды.
2)
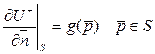
шекаралық шартын қанағаттандаратын 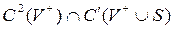 класында жататын
класында жататын 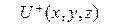 функциясын табуды Лаплас теңдеуіне қойылған екінші шекаралық есеп немесе ішкі Нейман есебі деп атайды. Мұндағы
функциясын табуды Лаплас теңдеуіне қойылған екінші шекаралық есеп немесе ішкі Нейман есебі деп атайды. Мұндағы 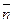 - S бетіне сырттай жүргізілген нормаль вектор, ал
- S бетіне сырттай жүргізілген нормаль вектор, ал 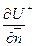 - деп
- деп 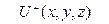 функциясының
функциясының 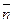 нормаль бағыты бойынша алынған туындысы белгіленген.
нормаль бағыты бойынша алынған туындысы белгіленген.
3)
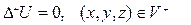
теңдеуін
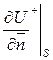
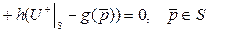
шекаралық шартын қанағаттандыратын 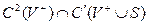 класына жататын
класына жататын 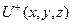 функциясын табуды Лаплас теңдеуіне қойылған үшінші шекаралық есеп деп атайды. Мысал ретінде радиусы
функциясын табуды Лаплас теңдеуіне қойылған үшінші шекаралық есеп деп атайды. Мысал ретінде радиусы 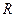 санына тең дөңгелектің шекарасында Дирихле шартын
санына тең дөңгелектің шекарасында Дирихле шартын
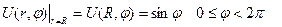
немесе
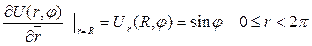
Нейман шартын қанағаттандыратын полярлық координата арқылы жазылған
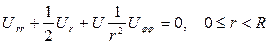
Лаплас теңдеуін қарастырайық. Егер осы есептердегі өте жұқа біртекті дискіде таралған температураға сәйкес келетін стационар процесті өрнектеген функцияны есептесек, онда дөңгелектің шекарасында Дирихле шарты 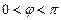 болған кезде оң
болған кезде оң 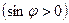 , ал
, ал 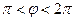 болған кезде теріс
болған кезде теріс 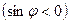 температура сақталатындығын, ал Нейман шарты
температура сақталатындығын, ал Нейман шарты 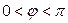 болған кезде жылу ағысы дөңгелек ішіне қарай, ал
болған кезде жылу ағысы дөңгелек ішіне қарай, ал 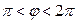 болған кезде дөңгелектің сыртына қарай бағытталғандығын көрсетеді. Пуассон теңдеуі үшін жоғарыда көрсетілгендей есептер ілгеріде қарастырылатын болғандықтан, оларға бұл пункте тоқталмаймыз.
болған кезде дөңгелектің сыртына қарай бағытталғандығын көрсетеді. Пуассон теңдеуі үшін жоғарыда көрсетілгендей есептер ілгеріде қарастырылатын болғандықтан, оларға бұл пункте тоқталмаймыз.
Стационар теңдеулер үшін жоғарыда қарастырылған шекаралық есептерден басқа шенелмеген 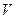 - облысында сыртқы есептер қарастырылады. Бұл есептерде бұрынғы шарттармен ізделінді функцияның шексіздіктегі тәртібіне қосымша шарттар қойылады. Жазықтықта қарастырылған шекаралық есептер мен кеңістікте қарастырылған шекаралық есептер үшін бұл шарт әртүрлі болады. Мысалы, Лаплас теңдеуі үшін сыртқы Дирихле есебі былай қойылады:
- облысында сыртқы есептер қарастырылады. Бұл есептерде бұрынғы шарттармен ізделінді функцияның шексіздіктегі тәртібіне қосымша шарттар қойылады. Жазықтықта қарастырылған шекаралық есептер мен кеңістікте қарастырылған шекаралық есептер үшін бұл шарт әртүрлі болады. Мысалы, Лаплас теңдеуі үшін сыртқы Дирихле есебі былай қойылады:
а) жазықтықта
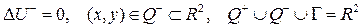
теңдеуін
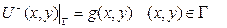
шартын қанағаттандыратын және 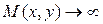 кезде шенелген
кезде шенелген 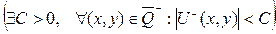
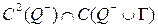 класына жататын
класына жататын 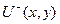 функциясын табуды Лаплас теңдеуіне жазықтықта қойылған сыртқы Дирихле есебі деп атайды.
функциясын табуды Лаплас теңдеуіне жазықтықта қойылған сыртқы Дирихле есебі деп атайды.
ә) кеңістікте
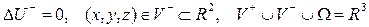
теңдеуін
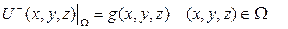
шартын қанағаттандыратын және 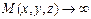 кезде нөлге бірқалыпты ұмтылатын (яғни
кезде нөлге бірқалыпты ұмтылатын (яғни 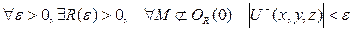 ).
).
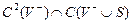 класында жататын
класында жататын 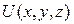 функциясын табуды Лаплас теңдеуіне кеңістікте қойылған сыртқы Дирихле есебі деп атайды.
функциясын табуды Лаплас теңдеуіне кеңістікте қойылған сыртқы Дирихле есебі деп атайды.
Лаплас теңдеуі үшін қойылатын сыртқы Нейман есебінің сыртқы Дирихле есебінен айырмашылығы ізделінді функцияға жазықтықта да, кеңістікте де 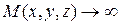 кезде бір ғана регулярлы болу шарты қойылады.
кезде бір ғана регулярлы болу шарты қойылады.
6.2.1 - анықтама.Ізделінді 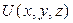 функциясы
функциясы 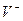 облысында регулярлы функция деп аталады, егер бір
облысында регулярлы функция деп аталады, егер бір 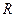 өте үлкен саны табылып,
өте үлкен саны табылып, 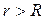 теңсіздігін қанағаттандыратын барлық
теңсіздігін қанағаттандыратын барлық 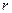 -лер үшін
-лер үшін
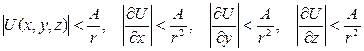 (
( 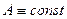 )
)
теңсіздіктері орындалатын болса, мұндағы 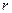 -саны
-саны 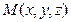 нүктесінің радиус –векторының модулі:
нүктесінің радиус –векторының модулі:
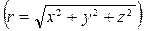
6.3. Дифференциалдық теңдеулер үшін шекаралық есептің корректілі қойылуы. Корректілі емес шекаралық есептерге мысалдар.Жоғарыда біз көптеген физикалық, механикалық құбылыстар дифференциалдық теңдеулер арқылы сипатталатындығын, бірақ дифференциалдық теңдеулер бұл құбылыстарды толық сипаттай алмайтындығын, оларды толық сипаттау үшін қосымша шарттар қажет екендігін көрдік. Мұндай қосымша шарттар ретінде көбінесе шекаралық және бастапқы шарттар қарастырылады. Табылған шешім қарастырылып отырған физикалық немесе басқа құбылыстардың жуық математикалық сипаттамасын береді, өйткені дербес туындылы дифференциалдық теңдеулер көмегімен физикалық, басқада құбылыстардың математикалық моделін құрған кезде, біз нақты құбылыстың моделін емес, ал оның негізгі белгілерін сақтайтын идеалды моделін жасауға мәжбүрміз. Сондықтан математикалық моделдеуден кейінгі алынған физикалық және басқада есептердің нәтижесі дәл бола алмайды. Осыған байланысты шекаралық есептің корректілі қойылуы ұғымы еңгізіледі.
Шекаралық есептің корректілі қойылуы ұғымын еңгізбей тұрып, осы ұғыммен байланысты шекаралық есептің шешімінің орнықтылығы жайлы ұғымды енгізейік.
6.3.1. – анықтама. Егер шекаралық есепте берілетін деректердің аз өзгерісі, оның шешімінің аз өзгерісін тудыратын болса, онда шекаралық есептің ондай шешімін орнықты шешім деп атайды.
6.3.2. – анықтама. Егер шекаралық есептің:
1) қандай да бір 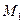 функциялар класында шешімі бар болса (шешімнің бар болу шарты);
функциялар класында шешімі бар болса (шешімнің бар болу шарты);
2) қандай да бір 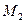 функциялар класында шешімі жалғыз болса (шешімнің жалғыз болу шарты);
функциялар класында шешімі жалғыз болса (шешімнің жалғыз болу шарты);
3) берілген деректердің аз өзгерісі шешімінің аз өзгерісін тудыратын болса (шешімнің орнықты болу шарты);
онда мұндай шекаралық есепті корректілі қойылған шекаралық есеп деп атайды.
Есептің шешімнің бар және жалғыз болу шарты, есептің берілгендерінің ішінде қайшылық жоқ және олар жалғыз шешімді бөліп алуға жеткілікті екендігін білдіреді. Кез келген нақты есептің берілгендері, көбінесе, егер олар эксперимент арқылы алынған болса, олардың мәндері жуықпен табылады. Сондықтан, берілгендердің аз өзгерісі шешімнің аз өзгерісіне әкелуі керек. Бұл жағдай шешімнің орнықтылық шартының қажеттілігін білдіреді.
6.3.2 – анықтамасының шарттарын қанағаттандыратын шекаралық есепті Адамар мағынасында корректілі қойылған, ал 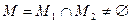 функциялар класын корректілік класы деп атайды.
функциялар класын корректілік класы деп атайды.
6.3.2.- анықтамасының кем дегенде бір шарты орындамайтын шекаралық есепті корректілі қойылмаған есеп деп атайды.
Енді корректілі қойылмаған есептерге мысалдар келтірейік.
6.3.1.- мысал. Ж. Адамар мысалы 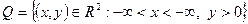 жарты жазықтығында
жарты жазықтығында
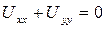
 (6.3.1)
(6.3.1)
Лаплас теңдеуінің
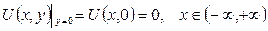 (6.3.2)
(6.3.2)
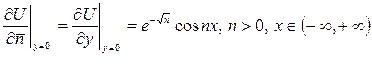 ( 6.3.3)
( 6.3.3)
бастапқы шарттарын қанағаттандыратын 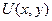 шешімін табу керек.
шешімін табу керек.
Математикалық физикада (6.3.1)-(6.3.3) есебін Лаплас теңдеуі үшін қойылған Коши есебі деп атайды. Тікелей қою арқылы
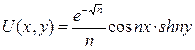 (6.3.4)
(6.3.4)
функциясының (6.3.1)-(6.3.3) есебінің шешімі болатындығын көрсету қиын емес. Мұндағы,
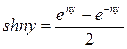
гиперболалық синус.
Бұл есепте шешімінің орнықтылығы шарты орындалмай тұр. Шынында, да (6.3.1) және (6.3.3) бастапқы шарттарынан 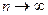 кезде
кезде
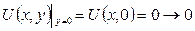
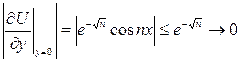
нөлге ұмтылатындарын көреміз. Бірақ (6.3.1)-6.3.3) есебінің шешімі болатын (6.3.4) функциясы үшін 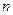 өте үлкен болғанда
өте үлкен болғанда 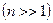
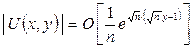
бағасы орындалады. Сондықтан, кез келген бекітілген  және
және 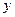
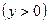 үшін
үшін 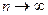 кезде
кезде 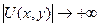 ұмтылады.
ұмтылады.
Сонымен, бастапқы шарттардың өте кішкентай өзгерісі Коши есебінің шешімнің өте үлкен өзгерісін тудырып тұр. Бұл Лаплас теңдеуіне қойылатын Коши есебінің корректілі қойылмайтындығын білдіреді. Лаплас теңдеуі эллиптикалық типті теңдеу болғандықтан, жалпы жағдайда, эллиптикалық типті теңдеулер үшін Коши есебі корректілі қойылмаған деген қортындыға келеміз.
6.3.2- мысал. 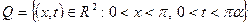 тік төртбұрышын қарастырайық. Мұндағы,
тік төртбұрышын қарастырайық. Мұндағы, 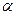 - оң иррационал сан.
- оң иррационал сан. 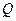 - тік төртбұрышында
- тік төртбұрышында
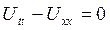 (6.3.5)
(6.3.5)
ішек тербелісінің теңдеуін
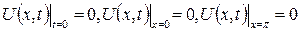 (6.3.6)
(6.3.6)
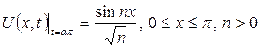 (6.3.7)
(6.3.7)
шекаралық шарттарын қанағаттандыратын 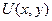 функциясын табу керек.
функциясын табу керек.
(6.3.5)-(6.3.7) есебін ішек тербелісіне қойылған Дирихле есебі деп атайды.
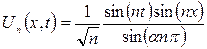 (6.3.8)
(6.3.8)
функциясы қарастырылып отырған есептің шешімі болады. Берілген 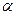 иррационал сан болғандықтан, нақты сандар теориясынан кез келген
иррационал сан болғандықтан, нақты сандар теориясынан кез келген 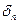 рационал саны үшін
рационал саны үшін
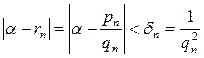 (6.3.9)
(6.3.9)
теңсіздігі орындалатындай
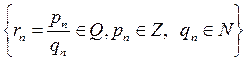 ,
,
рационал сандар тізбегі табылатындығы шығады. 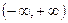 аралығында жататын кез келген
аралығында жататын кез келген  – тер үшін
– тер үшін
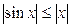
екендігін және (6.3.9) теңсіздігін ескеріп
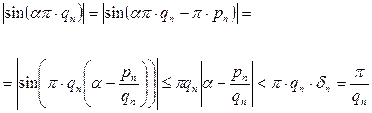 (6.3.10)
(6.3.10)
теңсіздігін аламыз. Осы теңсіздікті пайдаланып 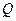 тік төртбұрышында жатқан кез келген бекітілген
тік төртбұрышында жатқан кез келген бекітілген 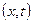 нүктелері үшін (6.3.8) функциясын төменнен бағалаймыз:
нүктелері үшін (6.3.8) функциясын төменнен бағалаймыз:
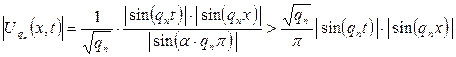
Бұдан 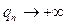 кезде
кезде 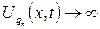 ұмытылатындығын көреміз. Демек,
ұмытылатындығын көреміз. Демек,
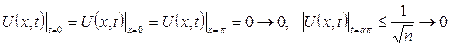 ,
, 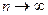
ұмтылатындығынан 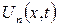 нөлге ұмтылмайтынын көреміз. Сондықтан бұл есепте де шешімнің орнықтылық шарты орындалмайды. Олай болса, ішек тербелісіне қойылатын Дирихле есебі корректілі емес.
нөлге ұмтылмайтынын көреміз. Сондықтан бұл есепте де шешімнің орнықтылық шарты орындалмайды. Олай болса, ішек тербелісіне қойылатын Дирихле есебі корректілі емес.
Ішек тербелісі теңдеуі гиперболалық типті теңдеудің қарапайым өкілі болғандықтан, гиперболалық типті теңдеуге қойылатын Дирихле есебі жалпы жағдайда корректілі қойылмаған деген қортындыға келеміз.
6.3.3 – мысал. 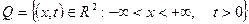 жарты жазықтығында
жарты жазықтығында
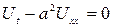 (6.3.11)
(6.3.11)
жылуөткізгіштік теңдеуін
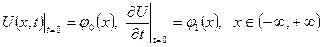 (6.3.12)
(6.3.12)
(мұндағы 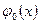 және
және 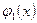 берілген өте тегіс функциялар) бастапқы шарттарын қанағаттандыратын
берілген өте тегіс функциялар) бастапқы шарттарын қанағаттандыратын 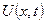 функциясын табу керек.
функциясын табу керек.
Шешімі. (6.3.11)-(6.3.12) теңдеуінің шешімі бар деп ұйғарайық. Онда берілген 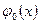 және
және 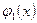 функциялары
функциялары 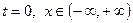 кезде
кезде
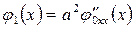 (6.3.13)
(6.3.13)
теңдігін қанағаттандыруы керек. Сондықтан тек (6.3.13) шарт орындылған кезде ғана (6.3.11)-(6.3.12) есебінің шешімі бар болуы мүмкін. Бірақ, 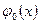 және
және 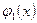 функциялары әр түрлі және ешқандай шарттармен байланысты емес, сондықтан жылуөткізгіштік теңдеуіне қойылатын екі шартпен берілген Коши есебі корректілі емес.
функциялары әр түрлі және ешқандай шарттармен байланысты емес, сондықтан жылуөткізгіштік теңдеуіне қойылатын екі шартпен берілген Коши есебі корректілі емес.
Ілгеріде, бір шартпен, яғни
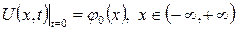 ,
,
мұндағы 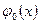 үзіліссіз және шенелген функция, берілген жылуөткізгіштік теңдеуіне қойылған Коши есебі корректілі болатынын көрсетеміз.
үзіліссіз және шенелген функция, берілген жылуөткізгіштік теңдеуіне қойылған Коши есебі корректілі болатынын көрсетеміз.
Корректілі қойылмаған есептер көбінесе практикада тікелей зерттеу мүмкін болмайтын объектілерді зерттеген кезде жиі кездеседі. Мысалы, жер асты қазба байлықтарын зерттеу кезінде. Мұндай зерттеу кезінде жер астындағы 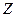 объектісінің қасиеттерін, экспериментальді өлшеуге мүмкін болатын,
объектісінің қасиеттерін, экспериментальді өлшеуге мүмкін болатын, 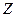 объектісі мен
объектісі мен 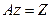 функционалдық түрде байланысатын, оның жер бетіне шығарылған
функционалдық түрде байланысатын, оның жер бетіне шығарылған 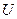 бөліктері арқылы зерттейді. Нәтижесінде кері есеп пайда болады. Ол
бөліктері арқылы зерттейді. Нәтижесінде кері есеп пайда болады. Ол 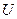 арқылы
арқылы 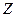 объектісін анықтау. Бұл есептердің көпшілігі корректілі қойылмаған есептер болады. Кері есептерді шешу теориясы Ресей ғалымдары А.Н.Тихонов пен М.М. Лаврентьев еңбектерінде құрылған.
объектісін анықтау. Бұл есептердің көпшілігі корректілі қойылмаған есептер болады. Кері есептерді шешу теориясы Ресей ғалымдары А.Н.Тихонов пен М.М. Лаврентьев еңбектерінде құрылған.
6.4. Коши есебі. Коши – Ковалевская теоремасы. 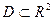 облысында анықталған
облысында анықталған
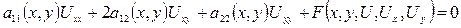 (6.4.1)
(6.4.1)
екінші ретті туындыларына байланысты сызықты дербес туындылы дифференциалдық теңдеуін қарастырайық. 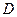 облысында түзетілетін, ұзындығы ақырлы
облысында түзетілетін, ұзындығы ақырлы 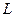 қисығы
қисығы
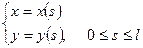
параметрлік түрде берілген болсын. Мұндағы 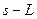 қисығының доғасының ұзындығы, ал
қисығының доғасының ұзындығы, ал 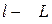 қисығының ұзындығы (21-сурет ).
қисығының ұзындығы (21-сурет ).
 Y
Y
 L
L
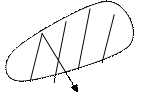 |
D
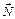
X
 0
0
21-cурет
Коши есебі. 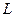 қисығының маңайында (6.4.1) теңдеуін және
қисығының маңайында (6.4.1) теңдеуін және
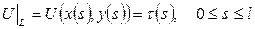 (6.4.2)
(6.4.2)
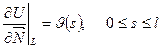 (6.4.3)
(6.4.3)
шекаралық шарттарын қанағаттандыратын 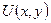 функциясын табу керек. Мұндағы
функциясын табу керек. Мұндағы 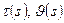 берілген өте тегіс функциялар,
берілген өте тегіс функциялар, 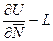 қисығына жүргізілген нормаль бойынша туынды. Дербес туындылы дифференциалдық теңдеулерге қойылатын Коши есебі шекаралық есептердің ішіндегі ең маңыздысы болып табылады.
қисығына жүргізілген нормаль бойынша туынды. Дербес туындылы дифференциалдық теңдеулерге қойылатын Коши есебі шекаралық есептердің ішіндегі ең маңыздысы болып табылады.
Коши – Ковалевская теоремасы. Егер (6.4.1) теңдеуінің коэффиценттері және 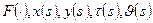 функциялары аналитикалық функциялар болса, онда (6.4.1) – (6.4.3) Коши есебінің
функциялары аналитикалық функциялар болса, онда (6.4.1) – (6.4.3) Коши есебінің 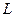 қисығы (6.4.1) теңдеуінің характеристикасы болмаған кезде
қисығы (6.4.1) теңдеуінің характеристикасы болмаған кезде 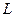 қисығының өте кішкентай маңайында жалғыз аналитикалық шешімі бар болады. Егер
қисығының өте кішкентай маңайында жалғыз аналитикалық шешімі бар болады. Егер 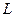 қисығы (6.4.1) теңдеуінің характеристикасы болса, онда жалпы жағдайда Коши есебі корректілі қойылмаған болады.
қисығы (6.4.1) теңдеуінің характеристикасы болса, онда жалпы жағдайда Коши есебі корректілі қойылмаған болады.
Мысалы, 6.3.-мысалында 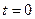 түзуі жылуөткізгіштік теңдеуінің характеристикасы, сондықтан Коши есебі корректілі қойылмаған.
түзуі жылуөткізгіштік теңдеуінің характеристикасы, сондықтан Коши есебі корректілі қойылмаған.
