Прямые и плоскости
Лекция 4. Декартова прямоугольная система координат на плоскости и в пространстве. Радиус-вектор точки, координаты точки; связь координат вектора с координатами его начала и конца. Простейшие задачи аналитической геометрии: вычисление длины отрезка, деление отрезка в данном отношении. Геометрический смысл уравнения 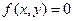 на плоскости и
на плоскости и 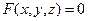 в пространстве. Различные виды уравнения прямой на плоскости: общее уравнение, параметрические уравнения, каноническое уравнение, уравнение прямой с угловым коэффициентом, уравнение прямой “в отрезках”. Нормальный и направляющий векторы прямой. Взаимное расположение двух прямых на плоскости. Вычисление угла между прямыми.
в пространстве. Различные виды уравнения прямой на плоскости: общее уравнение, параметрические уравнения, каноническое уравнение, уравнение прямой с угловым коэффициентом, уравнение прямой “в отрезках”. Нормальный и направляющий векторы прямой. Взаимное расположение двух прямых на плоскости. Вычисление угла между прямыми.
ОЛ-1, пп. 3.1–3.5, 4.1–4.3; ОЛ-3, гл. 2, §1 п. 9, гл. 4 §1, гл. 5, §1.
Лекция 5. Нормальное уравнение прямой. Расстояние от точки до прямой. Различные виды уравнения плоскости в пространстве: общее уравнение плоскости; уравнение плоскости, проходящей через три точки; уравнение плоскости “в отрезках”. *Связка плоскостей. Взаимное расположение двух плоскостей в пространстве. Угол между плоскостями. Нормальное уравнение плоскости Расстояние от точки до плоскости.
ОЛ-1, пп. 4.4, 5.1; ОЛ-3, гл. 5, §1, п. 7, §3.
Лекция 6. Прямая в пространстве. Общие уравнения прямой. Параметрические уравнения прямой; векторное уравнение прямой; канонические уравнения прямой. Уравнения прямой, проходящей через две заданные точки. Взаимное расположение прямой и плоскости, угол между прямой и плоскостью. Взаимное расположение двух прямых в пространстве, угол между прямыми в пространстве. Расстояние от точки до прямой в пространстве. Расстояние между двумя прямыми.
ОЛ-1, пп. 5.3–5.5; ОЛ-3, гл. 5, §4.
