Встроенные функции для работы с матрицами

Тема 1. Работа с массивами

1.1 Простейшие операции над матрицами

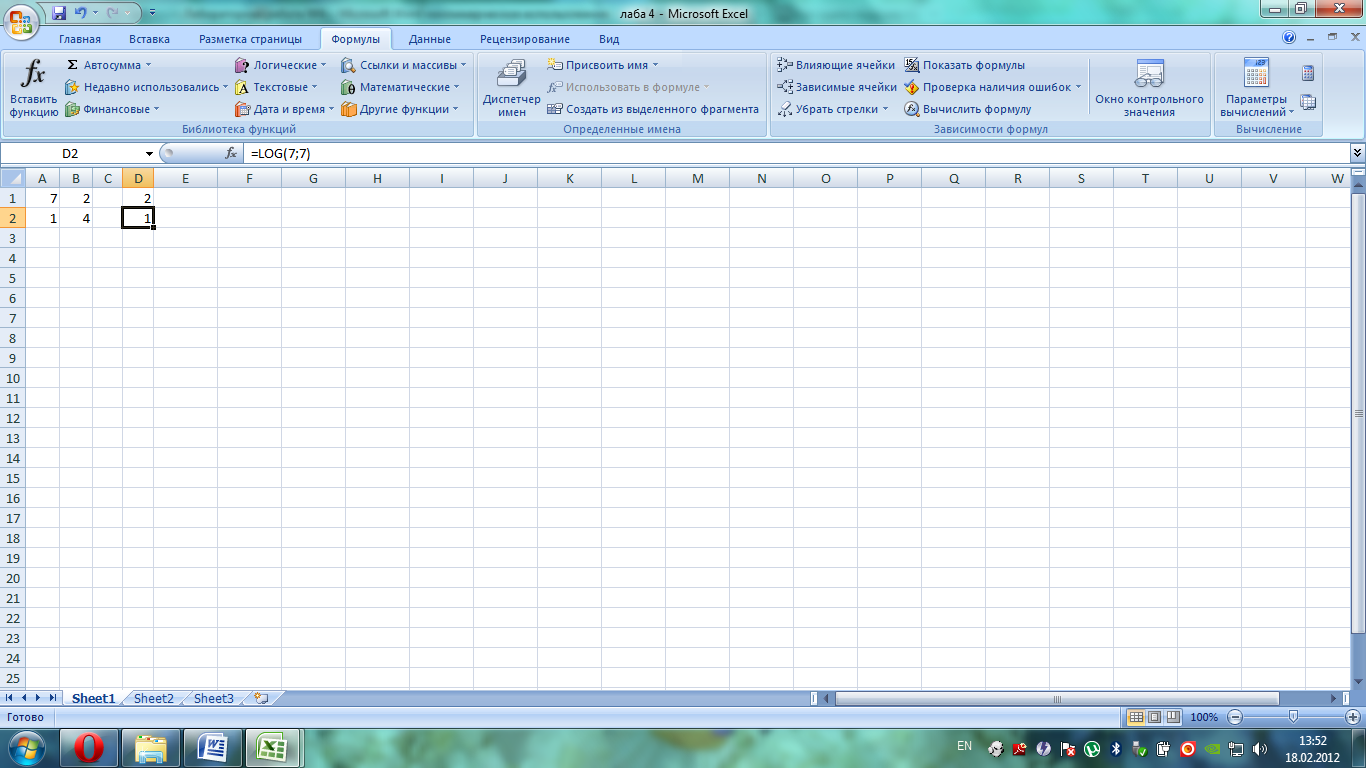
Пример 1. - Умножение массива А1:В2 на число 5:

1) В ячейку В2 ввела формулу =3* ;

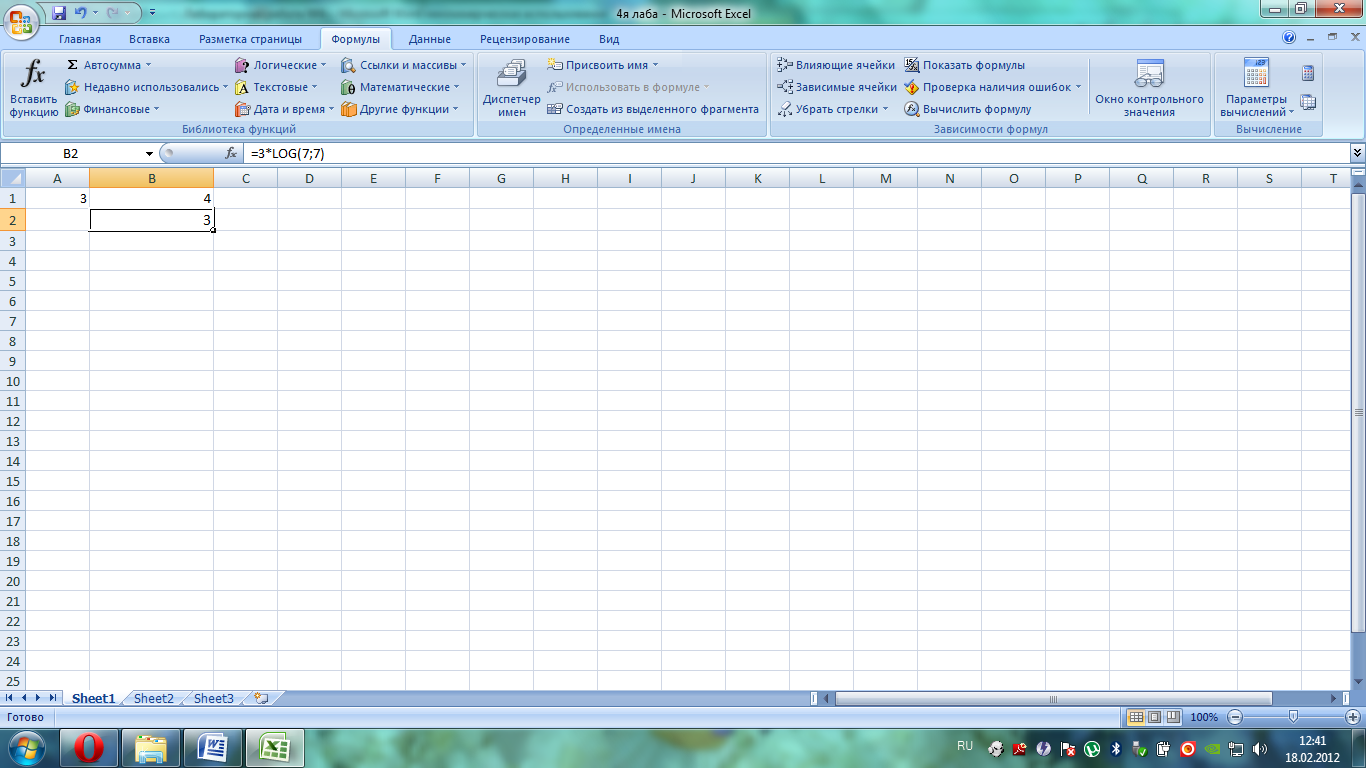
2) В ячейку А2 – формулу ;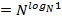

3) Выделила на рабочем листе область D1:E2 и ввела формулу =А1:В2*5 . Закончила ввод нажатием следующих клавиш – <Ctrl>+<Shift>+<Enter> - и получила следующий результат:

Пример 2. – Сумма (разность) массивов.

1) В ячейку В2 ввела формулу =2* ;

2) В ячейку А2 ввела формулу = ;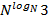

3) Выделила ячейки G1:H2, ввела формулу =A1:B2+D1:E2 и закончила ввод нажатием следующих клавиш – <Ctrl>+<Shift>+<Enter> - получила следующий результат:

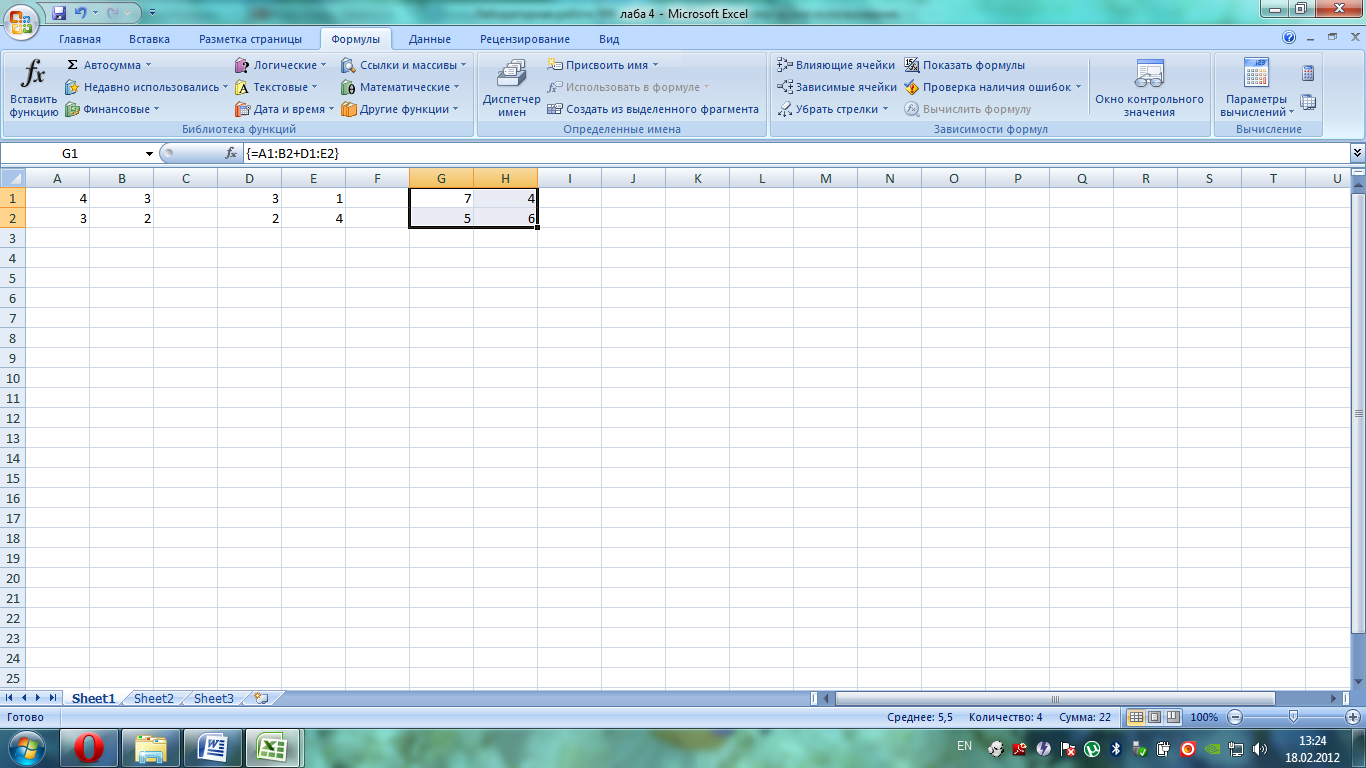
Пример 3. – Поэлементное произведение (деление) массивов.

1) Выделила ячейки G1:H2, ввела формулу =A1:B2*D1:E2 и закончила ввод нажатием следующих клавиш – <Ctrl>+<Shift>+<Enter> - получила следующий результат:

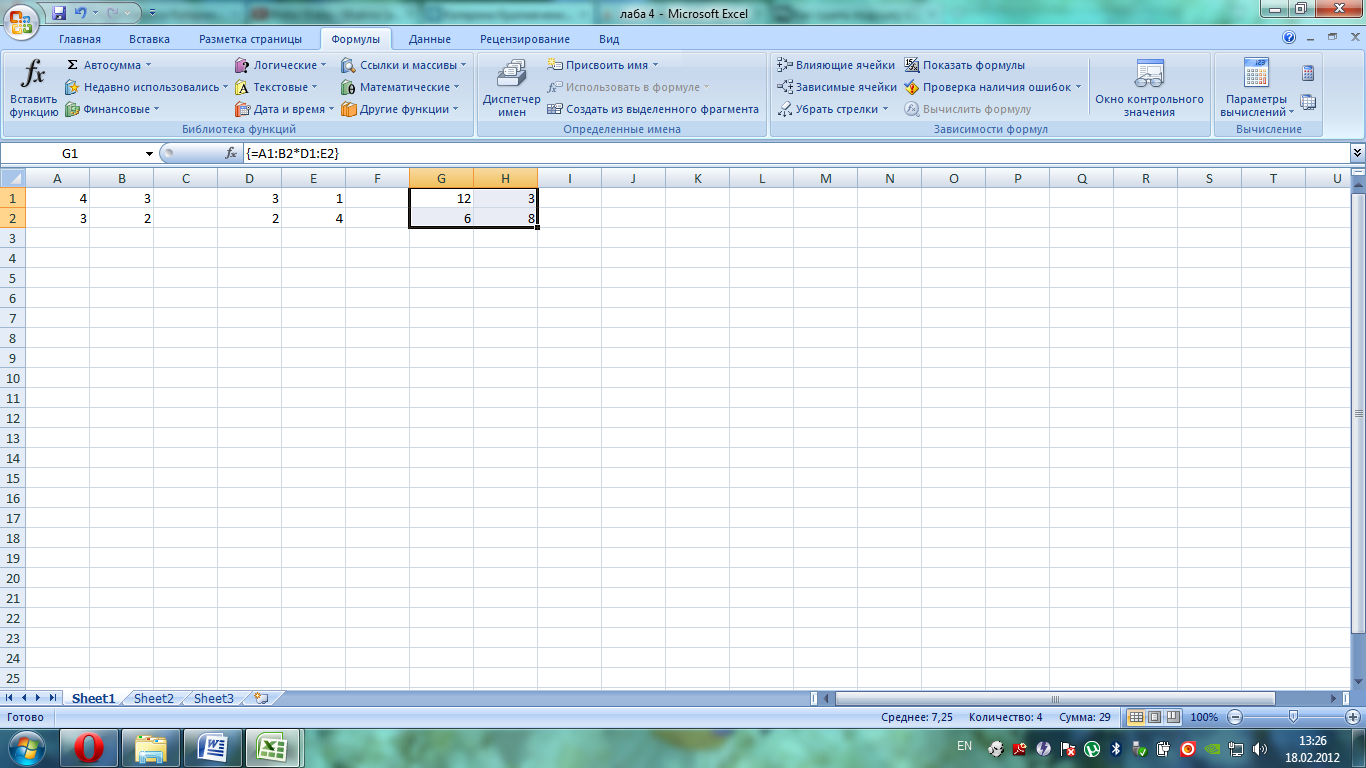
Пример 4. Массив, каждый элемент которого связан посредством некоторой функции с соответствующим элементом первоначального размера.

1) Выделила ячейки D1:E2, ввела формулу =SIN(A1:B2) и закончила ввод нажатием следующих клавиш – <Ctrl>+<Shift>+<Enter> - получила следующий результат:

Встроенные функции для работы с матрицами

Пример 5. Решим систему линейных уравнений с двумя неизвестными:

Чтобы решить данную систему линейных уравнений AX=B, где А – матрица коэффициентов системы, X – вектор-столбец неизвестных, В – вектор-столбец из свободных членов. а X = 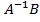, где обратная матрица А, поэтому для решения этой системы уравнений проведем следующие операции:

1) Выделила ячейки F1:F2 и ввела следующую формулу =МУМНОЖ(МОБР(A1:B2);D1:D2) , закончила ввод нажатием следующих клавиш – <Ctrl>+<Shift>+<Enter> - получила следующий результат:

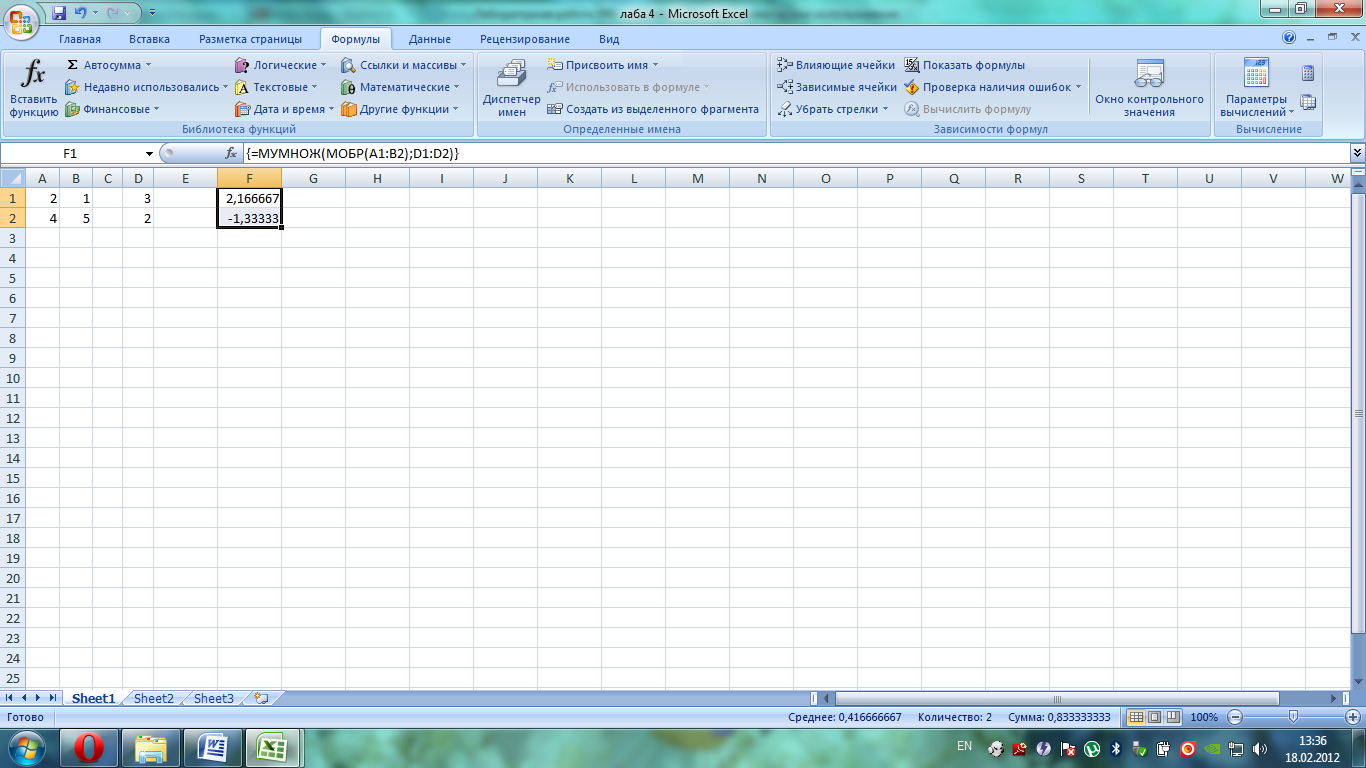
Пример 6. Решить систему линейных уравнений 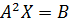, где

А= , B=

Для решения этой матрицы проведем следующие операции:

1) Введем в диапазон ячеек А1:В2 элементы матрицы А;

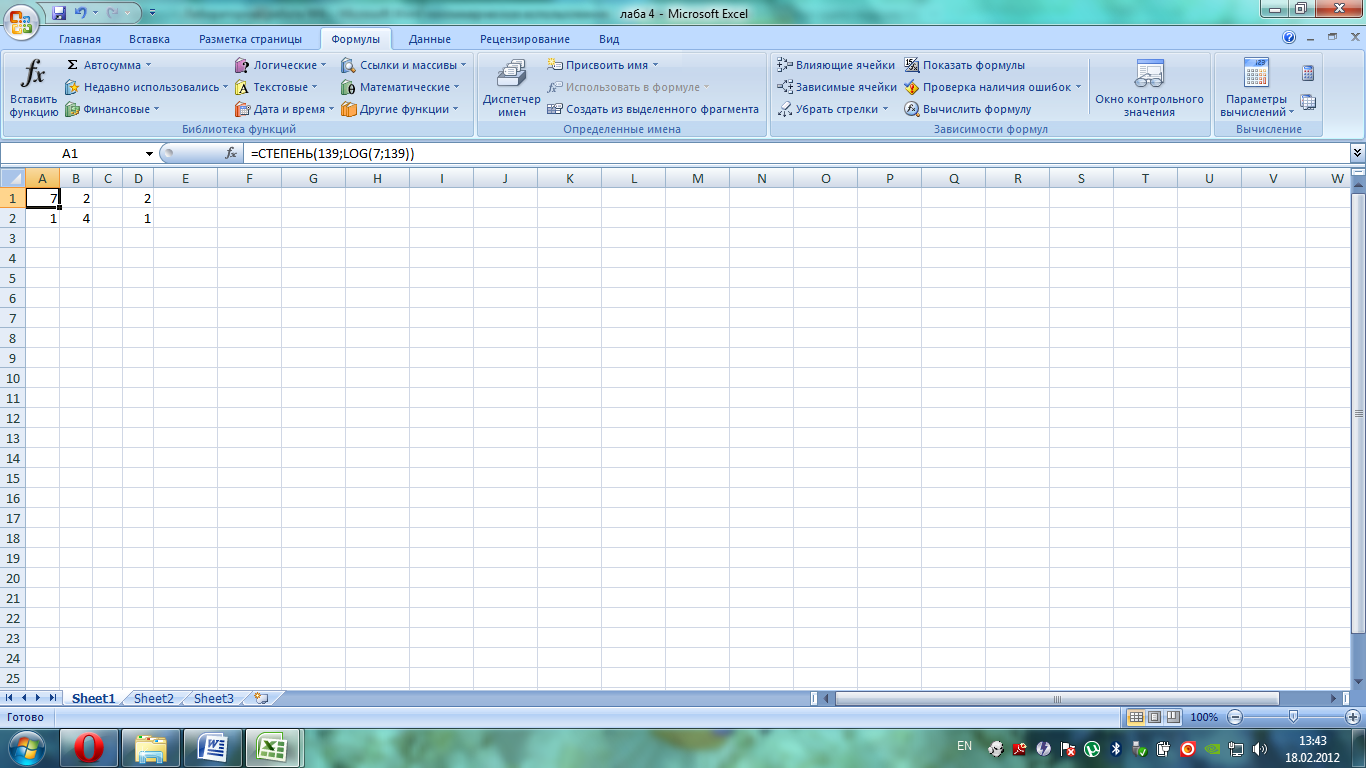
2) Введем в диапазон ячеек D1:D2 – элементы столбца свободных членов В;

2) Выделим диапазон F1:F2 куда введем следующую формулу =МУМНОЖ(МОБР(МУМНОЖ(A1:B2;A1:B2));D1:D2) . Закончить ввод нажатием следующих цифр – <Ctrl>+<Shift>+<Enter> . Получаем следующий результат:

Пример 7. Вычисление квадратичной формулы z= , где А – квадратичная матрица, введенная в диапазон А1:В2; Х – вектор, введенный в диапазон D1:D2, а символ (т) обозначает операцию транспонирования (все данные из примера 5).

Для вычисления данной формулы введем в ячейку F1 формулу -=МУМНОЖ(МУМНОЖ(ТРАНСП(D1:D2);A1:B2);D1:D2) – получаем:

Пример 8. Вычисление значения квадратичной формы Z= , где

А= , Y=

Для решения этой задачи надо ввести в диапазон ячеек А1:В2 элементы матрицы А, в диапазон D1:D2 элементы столбца Y, в ячейку F1 нужно ввести формулу =МУМНОЖ(ТРАНСП(D1:D2);МУМНОЖ(ТРАНСП(A1:B2);D1:D2)):