Решение задач линейного программирования симплекс-методом

4.8.1 Основные понятия и определения

Линейное программирование (ЛП) – наука о методах отыскания экстремальных значений линейной функции, на неизвестные которой наложены линейные ограничения.

Общая (математическая) формулировка задачи ЛП формулируется следующим образом. Требуется найти экстремум (максимум или минимум) линейной функции n переменных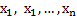

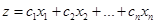(4.3)

При ограничениях, наложенных на переменные x вида

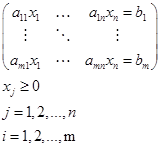(4.4)

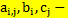заданные постоянные величины. (4.5)

Задача ЛП имеет так называемую каноническую форму, если система ограничений (4.4) задана в виде линейных уравнений, решения (4.5) системы неотрицательны и функция цели(4.3) при этом имеет экстремальное значение.

Базисные переменные – неизвестные, имеющие коэффициент, равный 1 в одном из уравнений системы (4.4) и не встречающиеся в остальных уравнениях системы (4.4) и в уравнении функции цели (4.3).

Базисное решение – решение, при котором все небазисные переменные равны 0.

4.8.2 Основные положения симплекс-метода

Для вычисления прежде всего необходимо, чтобы система ограничений (4.4) и уравнение функции цели (4.3) были приведены к виду, в котором какие-либо m неизвестных выражены через остальные n-m. При этом задача записывается в виде:

функция цели

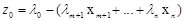(4.6)

система ограничений

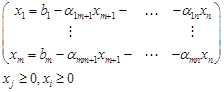(4.7)

где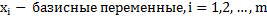

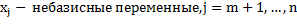
b, α, λ – постоянные коэффициенты, причем коэффициенты α и λ получаются после преобразования уравнения (4.3) и (4.4) к виду (4.6) и (4.7).

Допустим, что ищем решение системы, при котором функция цели (4.3) минимальна. Применяем базисное решение, то есть считаем, что

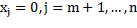тогда .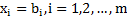

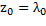При этом возможны два случая:

Все 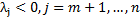. Тогда минимум функции достигается при 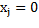и полученное базисное значение является оптимальным, задача решена.

Среди чисел 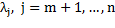, есть положительные, например 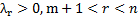. В этом случае значение функции цели можно уменьшить за счет увеличения переменной 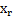, считая все остальные небазисные переменные равными 0, но так, чтобы ни одна из базисных переменных 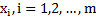не оказалась отрицательной. Получим

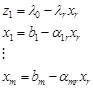
При этом, если все 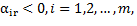то при всех 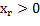, значения 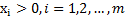а следовательно, при 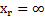, функция цели 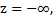т.е. минимум функции z не достигается (функция z снизу не ограничена).

Если среди чисел 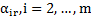, есть какое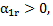-то то 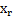увеличивать беспредельно нельзя, т.к. в этом случае базисная переменная 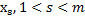может стать отрицательной. При нескольких положительных коэффициентах из 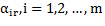раньше всех достигает нулевого значения та базисная переменная 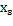, для которой .

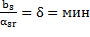Пусть .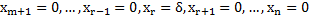

Найдем значения остальных неизвестных

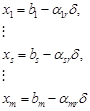
и целевой функции 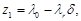причем уже .

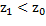Получен новый базис 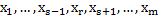, где 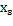заменено на 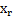и функция цели z уменьшилась.

Для окончания первого шага преобразования необходимо записать (4.6) и (4.7) через новый базис. Из уравнения для 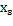(старого базисного неизвестного) в системе (4.7) находим 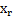(новое базисное неизвестное).

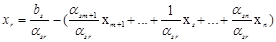
и подставляем это выражение вместо 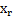в остальные уравнения. Получается система, разрешенная относительно нового базиса:

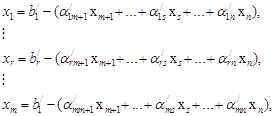(4.8)

А функция цели (4.8) через новые базисные переменные будет иметь вид

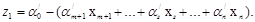(4.9)

В [2] приводятся правила определения коэффициентов 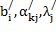системы (4.8) и (4.9) через коэффициенты системы (4.7).

Если исходное оптимальное решение не найдено, то процесс вычисления продолжается, производя аналогично вышеизложенному новую замену базиса.

Пример. Требуется найти максимум функции цели

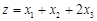
при заданных ограничениях

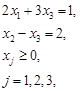
Выделим базисные переменные в системе ограничений, для этого разделим на коэффициент при 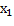первое уравнение ограничения.

Получим

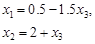
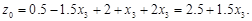
а функция цел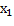и

и 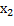образуют базис и базисное решение 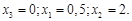При этом 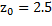. Поскольку 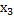входит в функцию цели с положительным коэффициентом ( 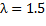) можно попытаться увеличить z за счет увеличения .

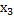Из первого уравнения следует, что 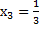, т.к. при 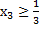значение 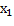становится отрицательным. Следовательно, необходимо перейти к новому базису .

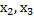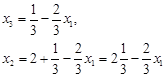
и функция цели

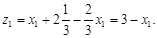
Функцию цели увеличить больше нельзя, т.к. 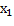входит в 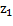с отрицательным коэффициентом.

Решение 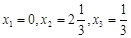является оптимальным базисным решением. Функция цели при этом достигает максимума