Молекулярная физика и термодинамика 8 страница
ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Сложение гармонических колебаний
Складываются взаимно перпендикулярные колебания. Установите соответствие между формой траектории и законами колебания точки 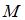 вдоль осей координат
вдоль осей координат 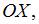
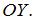
1. Прямая линия
2. Окружность
3. Фигура Лиссажу
 | 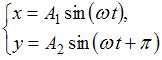 | ||
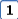 | 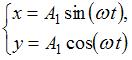 | ||
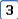 | 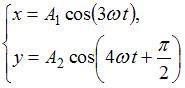 | ||
 |  |
Решение:
При одинаковой частоте колебаний вдоль осей 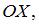
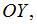 исключив параметр времени, можно получить уравнение траектории:
исключив параметр времени, можно получить уравнение траектории: 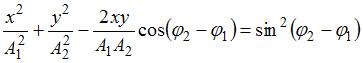 . Если разность фаз колебаний
. Если разность фаз колебаний 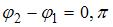 , то уравнение преобразуется к виду
, то уравнение преобразуется к виду 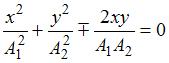 , или
, или 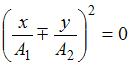 , что соответствует уравнению прямой:
, что соответствует уравнению прямой: 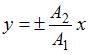 .
.
Если 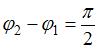 , то
, то 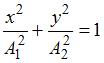 , что является уравнением эллипса, причем если амплитуды равны
, что является уравнением эллипса, причем если амплитуды равны 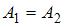 , то это будет уравнение окружности.
, то это будет уравнение окружности.
Если складываются колебания с циклическими частотами 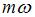 и
и 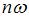 , где
, где 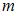 и
и 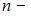 целые числа, точка
целые числа, точка  описывает сложную кривую, которую называют фигурой Лиссажу. Форма кривой зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний.
описывает сложную кривую, которую называют фигурой Лиссажу. Форма кривой зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний.
 ЗАДАНИЕ N 10 сообщить об ошибке
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Свободные и вынужденные колебания
Шарик, прикрепленный к пружине и насаженный на горизонтальную направляющую, совершает гармонические колебания.
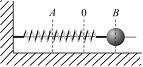
На графике представлена зависимость проекции силы упругости пружины на ось X от координаты шарика.
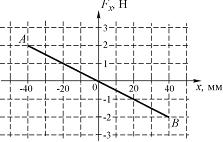
Работа силы упругости при смещении шарика из положения B в положение О (в мДж) составляет …
40 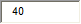 |
 ЗАДАНИЕ N 11 сообщить об ошибке
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Волны. Уравнение волны
На рисунке представлена мгновенная фотография электрической составляющей электромагнитной волны, переходящей из среды 1 в среду 2 перпендикулярно границе раздела АВ.
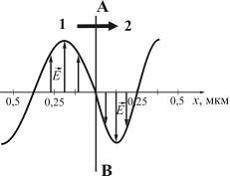
Если среда 1 – вакуум, то скорость света в среде 2 равна ______м/с.
 |  | 2,0·108 | |
 | 1,5·108 | ||
 | 2,4·108 | ||
 | 2,8·108 |
Решение:
Относительный показатель преломления двух сред равен отношению их абсолютных показателей преломления: 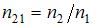 , где
, где 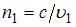 и
и 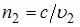 – абсолютные показатели преломления среды 1 и среды
– абсолютные показатели преломления среды 1 и среды 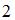 , равные отношению скорости
, равные отношению скорости 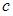 электромагнитной волны в вакууме к фазовым скоростям
электромагнитной волны в вакууме к фазовым скоростям 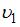 и
и 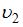 в этих средах. Следовательно,
в этих средах. Следовательно, 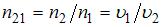 . Скорость волны
. Скорость волны 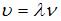 , где
, где 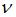 – частота;
– частота; 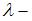 длина волны, которую можно определить, используя рисунок. Тогда при условии
длина волны, которую можно определить, используя рисунок. Тогда при условии 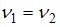 (при переходе электромагнитной волны из среды 1 в среду 2 частота не меняется) относительный показатель преломления равен:
(при переходе электромагнитной волны из среды 1 в среду 2 частота не меняется) относительный показатель преломления равен: 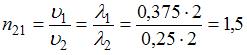 . Если среда 1 – вакуум, то
. Если среда 1 – вакуум, то 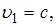 и
и 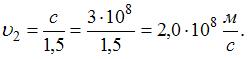
 ЗАДАНИЕ N 12 сообщить об ошибке
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Энергия волны. Перенос энергии волной
Если частоту упругой волны увеличить в 2 раза, не изменяя ее скорости, то интенсивность волны увеличится в ___ раз(-а).
4 |  |
Решение:
Интенсивностью волны называется скалярная величина, равная модулю среднего значения вектора плотности потока энергии (вектора Умова) 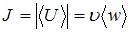 , где
, где 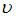 – скорость волны,
– скорость волны, 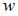 – объемная плотность ее энергии. Среднее значение объемной плотности энергии упругой волны определяется выражением
– объемная плотность ее энергии. Среднее значение объемной плотности энергии упругой волны определяется выражением 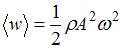 , где
, где 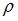 – плотность среды,
– плотность среды, 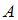 – амплитуда,
– амплитуда, 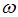 – циклическая частота волны. Тогда интенсивность волны равна
– циклическая частота волны. Тогда интенсивность волны равна 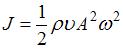 . Таким образом, если частоту упругой волны увеличить в 2 раза, не изменяя ее скорости, то интенсивность волны увеличится в 4 раза.
. Таким образом, если частоту упругой волны увеличить в 2 раза, не изменяя ее скорости, то интенсивность волны увеличится в 4 раза.
ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Энергия волны. Перенос энергии волной
Если частоту упругой волны увеличить в 2 раза, не изменяя ее скорости, то интенсивность волны увеличится в ___ раз(-а).
4 |  |
Решение:
Интенсивностью волны называется скалярная величина, равная модулю среднего значения вектора плотности потока энергии (вектора Умова) 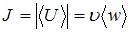 , где
, где 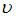 – скорость волны,
– скорость волны, 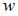 – объемная плотность ее энергии. Среднее значение объемной плотности энергии упругой волны определяется выражением
– объемная плотность ее энергии. Среднее значение объемной плотности энергии упругой волны определяется выражением 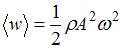 , где
, где 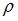 – плотность среды,
– плотность среды, 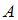 – амплитуда,
– амплитуда, 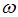 – циклическая частота волны. Тогда интенсивность волны равна
– циклическая частота волны. Тогда интенсивность волны равна 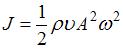 . Таким образом, если частоту упругой волны увеличить в 2 раза, не изменяя ее скорости, то интенсивность волны увеличится в 4 раза.
. Таким образом, если частоту упругой волны увеличить в 2 раза, не изменяя ее скорости, то интенсивность волны увеличится в 4 раза.
 ЗАДАНИЕ N 2 сообщить об ошибке
ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Сложение гармонических колебаний
Складываются два гармонических колебания одного направления с одинаковыми частотами и равными амплитудами 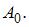 Установите соответствие между амплитудой результирующего колебания и разностью фаз складываемых колебаний.
Установите соответствие между амплитудой результирующего колебания и разностью фаз складываемых колебаний.
1. 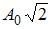
2. 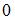
3. 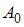
 | 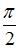 | ||
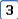 | 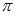 | ||
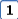 | 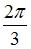 | ||
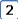 |
Решение:
Амплитуда результирующего колебания, полученного при сложении двух гармонических колебаний одного направления с одинаковыми частотами, определяется по формуле 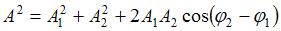 , где
, где 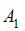 и
и 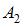 – амплитуды складываемых колебаний, (
– амплитуды складываемых колебаний, ( 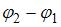 ) – разность их фаз. Если амплитуда результирующего колебания
) – разность их фаз. Если амплитуда результирующего колебания 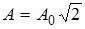 , то
, то 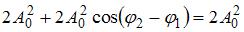 . Тогда
. Тогда 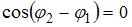 и разность фаз будет равна
и разность фаз будет равна 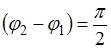 .
.
Если 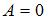 , то
, то 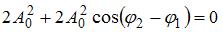 .Тогда
.Тогда 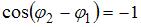 , следовательно,
, следовательно, 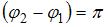 .
.
Если 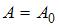 , то
, то 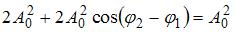 . Тогда
. Тогда 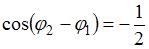 ; следовательно,
; следовательно, 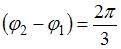 .
.
 ЗАДАНИЕ N 3 сообщить об ошибке
ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Свободные и вынужденные колебания
Шарик, прикрепленный к пружине и насаженный на горизонтальную направляющую, совершает гармонические колебания.

На графике представлена зависимость проекции силы упругости пружины на ось X от координаты шарика.

Работа силы упругости при смещении шарика из положения B в положение О (в мДж) составляет …
40 |  |
Решение:
Работу силы упругости можно найти, определив площадь под графиком функции на участке ВО. 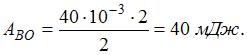 Работа положительна, так как шарик возвращается в положение равновесия.
Работа положительна, так как шарик возвращается в положение равновесия.
 ЗАДАНИЕ N 4 сообщить об ошибке
ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Волны. Уравнение волны
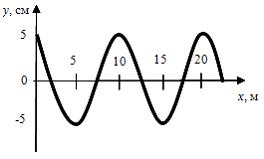
На рисунке представлен профиль поперечной упругой бегущей волны. Согласно рисунку значение волнового числа (в 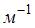 ) равно …
) равно …
 |  |  | |
 | 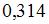 | ||
 | 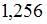 | ||
 | 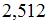 |
ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Волны. Уравнение волны
На рисунке представлен профиль поперечной упругой бегущей волны. Согласно рисунку значение волнового числа (в 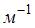 ) равно …
) равно …

 |  | 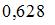 | |
 | 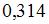 | ||
 | 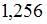 | ||
 | 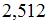 |
Решение:
Волновое число 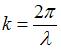 , где
, где 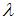 – длина волны, величину которой можно найти из графика:
– длина волны, величину которой можно найти из графика: 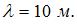 Следовательно,
Следовательно, 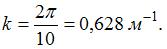
 ЗАДАНИЕ N 8 сообщить об ошибке
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Сложение гармонических колебаний
Резистор с сопротивлением 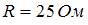 , катушка с индуктивностью
, катушка с индуктивностью 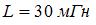 и конденсатор с емкостью
и конденсатор с емкостью 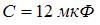 соединены последовательно и подключены к источнику переменного напряжения, изменяющегося по закону
соединены последовательно и подключены к источнику переменного напряжения, изменяющегося по закону 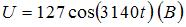 .
.
Установите соответствие между элементом цепи и эффективным значением напряжения на нем.
1. Сопротивление
2. Катушка индуктивности
3. Конденсатор
 | 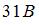 | ||
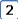 | 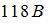 | ||
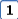 | 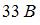 | ||
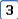 | 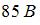 |
Решение:
Индуктивное, емкостное и полное сопротивления цепи равны соответственно: 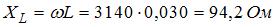 ,
, 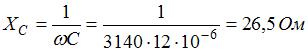 ,
, 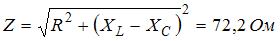 . Максимальное значение тока в цепи
. Максимальное значение тока в цепи 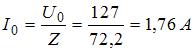 . Эффективное значение тока
. Эффективное значение тока 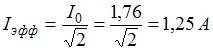 . Тогда искомые падения напряжений на элементах цепи равны:
. Тогда искомые падения напряжений на элементах цепи равны: 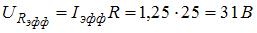 ,
, 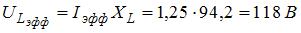 ,
, 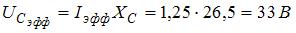 .
.
 ЗАДАНИЕ N 9 сообщить об ошибке
ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Энергия волны. Перенос энергии волной
Плоская электромагнитная волна распространяется в диэлектрике с проницаемостью 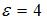 . Если амплитудное значение электрического вектора волны
. Если амплитудное значение электрического вектора волны 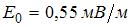 , то интенсивность волны равна …
, то интенсивность волны равна …
(Электрическая постоянная равна 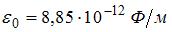 .
.
Полученный ответ умножьте на 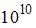 и округлите до целого числа.)
и округлите до целого числа.)
8 |  |
Решение:
Интенсивностью волны называется скалярная величина, равная модулю среднего значения вектора плотности потока энергии (вектора Умова – Пойнтинга) 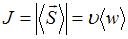 , где
, где 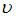 – скорость волны,
– скорость волны, 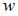 – объемная плотность ее энергии. Среднее значение объемной плотности энергии электромагнитной волны определяется выражением
– объемная плотность ее энергии. Среднее значение объемной плотности энергии электромагнитной волны определяется выражением 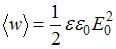 , а скорость волны в среде
, а скорость волны в среде 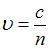 , где
, где 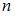 – абсолютный показатель преломления среды, причем
– абсолютный показатель преломления среды, причем 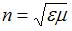 . Для неферромагнитных сред
. Для неферромагнитных сред 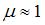 . Таким образом, выражение для интенсивности электромагнитной волны можно представить в виде
. Таким образом, выражение для интенсивности электромагнитной волны можно представить в виде 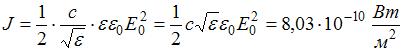 .
.
 ЗАДАНИЕ N 10 сообщить об ошибке
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Свободные и вынужденные колебания
На рисунках изображены зависимости от времени координаты и ускорения материальной точки, колеблющейся по гармоническому закону.
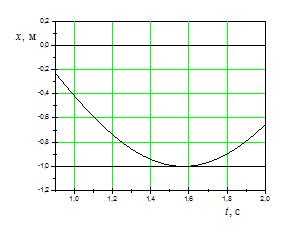
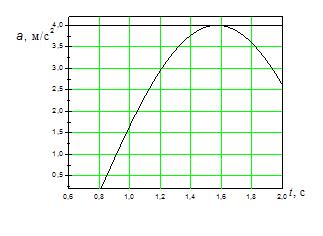
Циклическая частота колебаний точки равна …
2  |
 ЗАДАНИЕ N 5 сообщить об ошибке
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Волны. Уравнение волны
Электромагнитная волна частоты 3,0 МГц переходит из вакуума в диэлектрик с проницаемостью 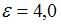 . При этом ее длина волны уменьшится на _____ м.
. При этом ее длина волны уменьшится на _____ м.
 |  | ||
 | |||
 | 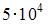 | ||
 | 0,50 |
Решение:
Длина волны связана со скоростью ее распространения соотношением: 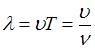 , где
, где 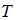 – период,
– период, 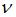 – частота волны. При переходе электромагнитной волны из вакуума в среду с показателем преломления
– частота волны. При переходе электромагнитной волны из вакуума в среду с показателем преломления 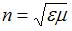 ее скорость уменьшается
ее скорость уменьшается 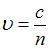 , частота не изменяется. Следовательно, длина волны уменьшается. Если длина волны в вакууме
, частота не изменяется. Следовательно, длина волны уменьшается. Если длина волны в вакууме 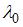 , а длина волны в среде
, а длина волны в среде 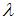 , то уменьшение длины волны составит
, то уменьшение длины волны составит 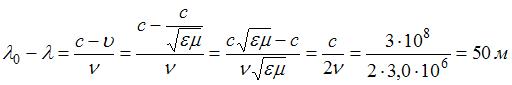 .
.
Здесь учтено, что магнитная проницаемость неферромагнитных сред 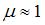 .
.
 ЗАДАНИЕ N 6 сообщить об ошибке
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Свободные и вынужденные колебания
Маятник совершает вынужденные колебания со слабым коэффициентом затухания 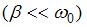 , которые подчиняются дифференциальному уравнению
, которые подчиняются дифференциальному уравнению 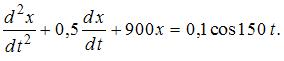 Амплитуда колебаний будет максимальна, если частоту вынуждающей силы уменьшить в _____ раз(-а).
Амплитуда колебаний будет максимальна, если частоту вынуждающей силы уменьшить в _____ раз(-а).
5 | 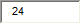 |
Решение:
Дифференциальное уравнение вынужденных колебаний имеет вид 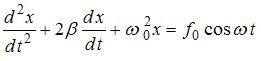 , где
, где 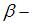 коэффициент затухания,
коэффициент затухания, 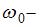 собственная круговая частота колебаний;
собственная круговая частота колебаний; 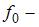 амплитудное значение вынуждающей силы, деленное на массу;
амплитудное значение вынуждающей силы, деленное на массу; 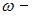 частота вынуждающей силы. При слабом затухании (коэффициент затухания значительно меньше собственной частоты колебаний маятника) амплитуда колебаний будет максимальна, если частота вынуждающей силы совпадет с собственной частотой колебаний маятника (явление резонанса). Собственная частота колебаний равна:
частота вынуждающей силы. При слабом затухании (коэффициент затухания значительно меньше собственной частоты колебаний маятника) амплитуда колебаний будет максимальна, если частота вынуждающей силы совпадет с собственной частотой колебаний маятника (явление резонанса). Собственная частота колебаний равна: 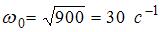 , частота вынуждающей силы
, частота вынуждающей силы 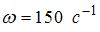 . Следовательно, частоту вынуждающей силы необходимо уменьшить в 5 раз.
. Следовательно, частоту вынуждающей силы необходимо уменьшить в 5 раз.
