Проверка местной устойчивости стенки балки
Местная устойчивость стенок подкрановых балок проверяется также, как и у обычных балок. Условная гибкость стенки: 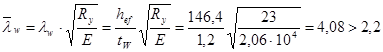 . Необходимо установить поперечные ребра жесткости с шагом не более 2hw = 2
. Необходимо установить поперечные ребра жесткости с шагом не более 2hw = 2 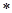 1,464 = 2,928 (м) при
1,464 = 2,928 (м) при 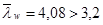 . Принимаем шаг 2 м.
. Принимаем шаг 2 м.
Ширина ребра bh 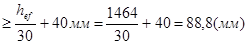 , принимаем bh = 90 мм.
, принимаем bh = 90 мм.
Толщина ребра: tS 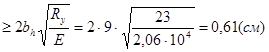 , принимаем tS = 8 мм.
, принимаем tS = 8 мм.
Размеры ребер жесткости приняты согласно п.7.10 [1]. Необходима проверка устойчивости, т.к. 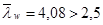 (наличие местных напряжений (sloc
(наличие местных напряжений (sloc 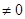 ) в балках с двусторонними поясными швами).
) в балках с двусторонними поясными швами).
Согласно п.7.6 [1] расчет на устойчивость стенок балок симметричного сечения, укрепленных только поперечными ребрами жесткости при наличии местн. напряж-я следует выполнять по ф-ле:
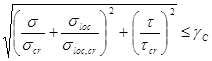 ,
,
где 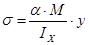 ,
, 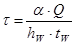 - действующие нормальные и касательные напряжения;
- действующие нормальные и касательные напряжения;
М и Q – средние значения соответственно момента и поперечной силы в пределах отсека;
a = 1,05 – для балок пролетом 12м;
scr и tcr – критические нормальные и касательные напряжения;
у = h0 / 2 = 1482 / 2 = 741(мм) = 74,1(см); h0=1500-18=1482 (мм).
Необходима проверка крайнего и среднего отсеков.
Крайний отсек.
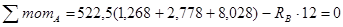 è
è 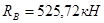 ;
;
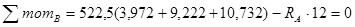 è
è 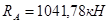 .
.
I – участок:
Q = RA = 1041,78 кН;
M = RA*x; М(0)=0; М1(0,536)=558,39 кН; М2(1,268)=1320,98 кН.
II – участок:
Q = RA – 522,5 = 519,28 (кН);
М = RA(1,268 + x) –522,5*х = 0; М(0)=1320,98 кН; М3(0,732)=1701,09 кН;М(1,51)=2105,09 кН.
III – участок:
Q = RA – 522,5*2 = -3,22 (кН);
М = RA(2,778 + х) –522,5(1,51 + х) –522,5*х = 0; М(0)=2105,09 кН; М(5,25)=2088,16 кН.
IV – участок:
Q = -RВ = -525,72 кН;
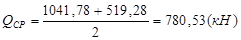 ,
, 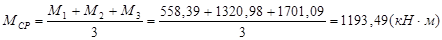
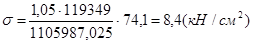 ,
, 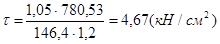 .
.
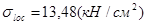 - см. "проверка прочности сечений";
- см. "проверка прочности сечений";
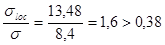 - табл.24, [1];
- табл.24, [1];
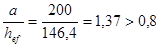 ;
; 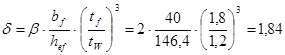 ;
;
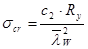 , где с2 = 51,66 (табл.25, [1]);
, где с2 = 51,66 (табл.25, [1]);
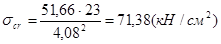 ,
,
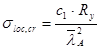 , где с1 = 30,374 (табл.23, [1]),
, где с1 = 30,374 (табл.23, [1]), 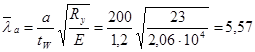 ;
;
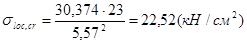 ;
;
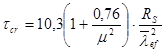 , где m - отношение большей стороны пластинки к меньшей;
, где m - отношение большей стороны пластинки к меньшей;
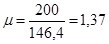 ; RS = 0,58*23 = 13,34 (кН/см2) – расчетное сопротивление сдвигу.
; RS = 0,58*23 = 13,34 (кН/см2) – расчетное сопротивление сдвигу.
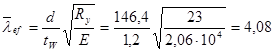 ,
,
где d = 146,4 см – меньшая из сторон пластинки (hef или а);
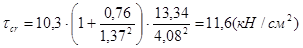 .
.
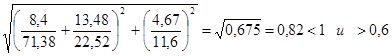 .
.
Средний отсек.
Построим эпюры М и Q.
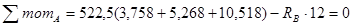 è
è 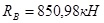 ;
;
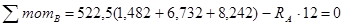 è
è 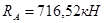 .
.
I – участок:
Q = RA = 716,52 кН;
M = RA*x; М(0)=0;М(3,758)=2692,68 кН.
II – участок:
Q = RA – 522,5 = 194,02 (кН);
М = RA(3,758 + x) –522,5*х = 0; М(0)=2692,68 кН; М(1,51)=2985,65 кН.
III – участок:
Q = RA – 522,5*2 = -328,48 (кН);
М = RA(5,268 + х) –522,5(1,51 + х) –522,5*х = 0; М(0)=2985,65 кН; М(5,25)=1261,13 кН.
IV – участок:
Q = -RВ = -850,98 кН;
Q = 194,02 кН; МСР = 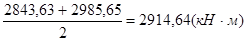 ;
;
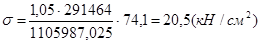 ,
, 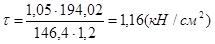 .
.
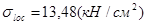 ;
; 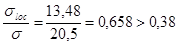 ;
;
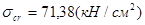 ,
, 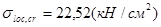 ;
; 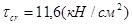 .
.
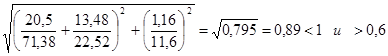 .
.
Q = 328,48 кН; МСР = 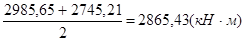 ;
;
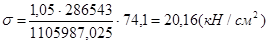 ,
, 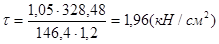 .
.
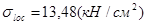 ;
; 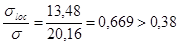 ;
;
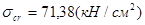 ,
, 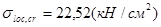 ;
; 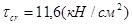 .
.
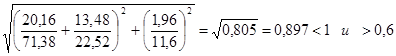 .
.
Расчет соединения поясов подкрановой балки со стенкой.
Соединение поясов подкрановой балки со стенкой осуществляется поясными швами. Швы делают сплошными , одинаковой наименьшей допустимой толщины по всей длине балки. Швы выполняем двусторонние, автоматической сваркой в лодочку сварочной проволокой СВ-0,8А.
Определим толщину шва (соединение стенки с верхним поясом):
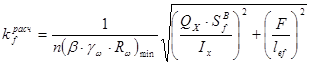
Rwf = 18 (кН/см2) – расчетное сопротивление угловых швов срезу по металлу шва (табл.56,[1]).
Rwz = 0,45Run = 0,45*36=16,2 (кН/см2) – то же, по металлу границы сплавления.
kfmin = 7 (мм) – (табл.38, [1]).
bf = 1,1, bz = 1,15 – кэффициенты проплавления шва (табл.34,[1]).
bf*gwf*Rwf = 1,1*1*18=19,8 (кН/см2).
bz*gwz*Rwz = 1,15*1*16,2=18,63 (кН/см2) – min
где gwf, gwz = 1 – коэффициенты условий работы шва.
QX = 1163,4 кН – по линии влияния Qmax.
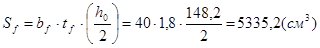 - статический момент пояса балки;
- статический момент пояса балки;
IX = 1105987,025см4 – момент инерции сечения балки;
lef = 35,52 см – длина распределения нагрузки от пояса на стенку;
F = 522,5 кН – расчетное значение вертикальной силы;
n = 2 – при двусторонних швах;
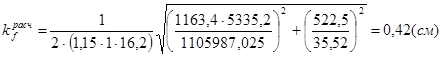 ,
,
kf 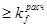 , kf
, kf 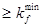 , принимаем kf = 7 мм.
, принимаем kf = 7 мм.
Соединение стенки с нижним поясом:
Вертикальные силы не действуют на нижний пояс, поэтому F = 0, следовательно:
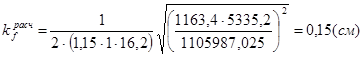 .
.
Принимаем: kf 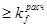 , kf
, kf 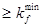 , è kf = 7 мм.
, è kf = 7 мм.
Расчет опорного ребра.
Балка опирается с помощью торцевых диафрагм. Торцы диафрагмы фрезеруются для непосредственной передачи опорного давления на оголовок колонны или опорный столик.
Размер опорных ребер торцевых диафрагм определяется из расчета на смятие:
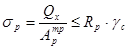 ;
;
где RP = Run/gm = Ru = 35 (кН/см2) – расчетное сопротивление стали смятию торцевой поверхности (табл.1, [1]).
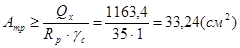 ,
,
принимаем Ah = bh*th = 22*1,6 =35,2 (см2) > АТР = 33,24 см2 .
Проверка местной устойчивости ребра (п.п.7.24, табл.30, [1]):
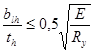 , где blh =
, где blh = 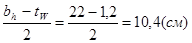 ;
;
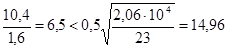 .
.
Проверка условной стойки:
А = Аh + tw*S = 35,2+1,2*23,34 = 63,21 (см2),
где 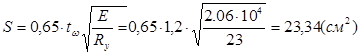 - часть стенки включающаяся в совместную работу с ребром;
- часть стенки включающаяся в совместную работу с ребром;
Момент инерции условной стенки относительно оси стенки (из плоскости балки):
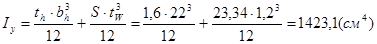 ,
,
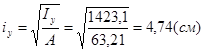 - радиус инерции.
- радиус инерции.
Проверим условную стойку на устойчивость из плоскости стенки:
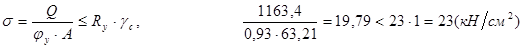
где jу = 0,930 – коэффициент продольного изгиба стойки (табл.72, [1]).
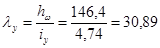 .
.
