Волноводы

В электротехнике передача волн на небольшие расстояния осуществляется возбуждением электромагнитных полей в трубах (металлических) различного сечения, именуемых волноводами.

Для простоты рассмотрим волновод прямоугольного сечения со стенками из идеального проводника. Т.к. в идеальном проводнике отсутствует электромагнитные и электрические поля, то

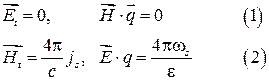
Предположим, что .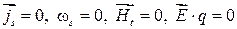

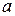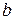Пусть стороны прямоугольника равны и , где .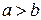

Ромич втыкай рисунок

Пусть в волновод в плоскости 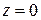поступает плоская электромагнитная волна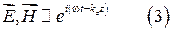

Подставляя (3) в волновые уравнения

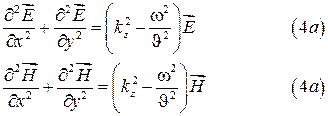
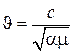
Здесь 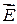и 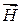неизвестные функции координат 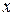и 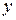, т.к. зависимость 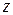и 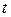уже определена.

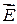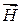Связь между и определяется уравнениями:

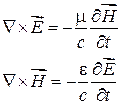
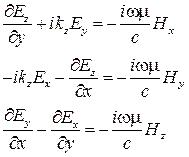
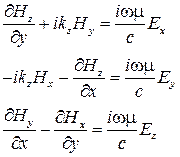
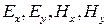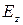Выражая далее через и 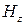находим:

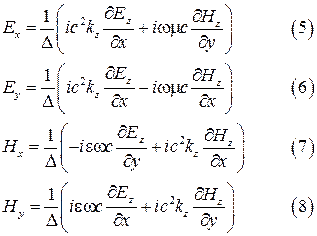
Будем искать решение 4а и 4б в виде поперечных плоских волн, то есть положим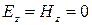

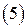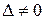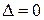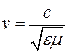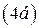Из видно, что компоненты поля равны нулю только в случае, если . Если определитель , как для плоской монохроматической волны в неограниченной среде ( ), то дает:

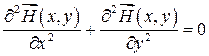
― двухмерное уравнение Лапласа на всей замкнутой границе области, то есть на сторонах прямоугольника ( ), магнитное поле направлено по касательной к границе, известно, что его единственное решение 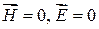. Значит поперечные волны не могут распространяться в прямоугольном волноводе с идеальными стенками. Этот вывод также относится к любому волноводу в виде простой трубы произвольного сечения, однако он не относится к случаю, когда границы области не замкнуты, а также к случаю несвязных систем (два концентрических цилиндра).

В поперечной волне волновода линии магнитного поля должны быть направлены по касательной к стенкам, и быть замкнутыми. Они не входят в идеальный проводник и не охватывают ток проводимости, продольная компонента тока смещения отсутствует, поэтому магнитные линии не охватывают линии тока смещения. Однако из общих соображений магнитные линии не охватывают никаких линий с током. В несвязной системе магнитные линии существовать не могут.

В рассмотренном волноводе возможно распространение плоских волн, которое не может существовать в неограниченном пространстве. Рассмотрим две независимые возможности:

1)

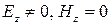
2) .

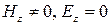1) Магнитное поле имеет две компоненты ― 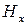и 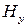и является чисто поперечным, а такие волны называются 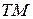-волнами или поперечно-магнитного типа.

2) Электрическое поле имеет поперечный характер.

Для 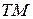-волны имеем

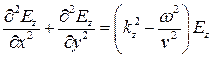
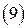
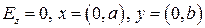
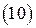
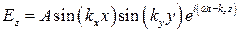
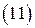
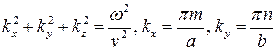
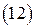
Найденное решение имеет вид волн, бегущих в направлении 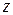и стоячих в плоскости 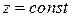. 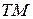-волну, отвечающую числам 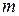и 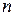, обозначают 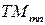. Если 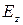известно, то из формул легко найти остальные компоненты поля. Автоматически будут выполняться и граничные условия. У стенок волновода линии магнитного поля тангенциальны к поверхности и замкнуты, охватывая продольные линии электрического поля.

Рассмотрим следствие из формулы 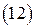. При заданных 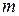и 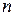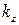имеет вещественные значения только, если

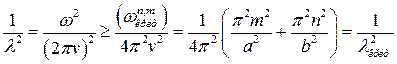
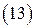
где 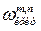― некоторая критическая частота, а 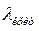― соответствующая ей длина волны. Так как минимальным 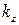отвечает затухающая по экспоненциальному закону волна, то через волновод проходят только волны с частотой 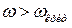. Наибольшее значение длины проходящей волны отвечает 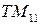-волне ― это 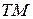-волна наименьшего порядка и для неё: 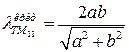. Фазовая скорость

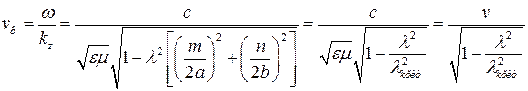
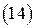
Так как 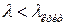, то фазовая скорость волны в волноводе всегда больше скорости света 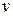в неограниченной среде и при 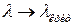неограниченно возрастает. В частности, если в волноводе не введен диэлектрик, то есть 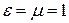, то 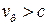.