Техническая диагностика. Математические основы технической диагностики.

Основные задачи и принципы технической диагностики (ТД) машин и оборудования: Надежность технических систем (ТС). Методы поддержания и сохранения надежности работоспособности. Система технического обслуживания (ТО) и ремонтов. Переход на новый принцип обслуживания машин и оборудования по фактическому состоянию. Основные задачи ТД.

ТД - это наука о распознавании состояния ТС. ТД изучает методы получения и оценки диагностической информации, диагностической модели и алгоритмы принятия решений. Целью ТД является повышение надежности и ресурса ТС. Как известно, наиболее важным показателем надежности является отсутствие отказов во время функционирования ТС. ТД благодаря раннему обнаружению дефектов и неисправностей позволяет устранить подобные отказы в процессе ТО, что повышает надежность и эффективность эксплуатации, а также дает возможность эксплуатации ТС ответственного назначения по состоянию.

ТД решает обширный круг задач, многие из которых являются смежными с задачами других научных дисциплин. Основной задачей ТД является распознавание ТС в условиях ограниченной информации.

Теоретическим фундаментом для решения основной задачи ТД следует считать общую теорию распознавания образцов. Эта теория занимается распознаванием образов, машинным образованием речи и т.д. ТД изучает алгоритмы распознавания применительно к задачам диагностики. Алгоритмы распознавания в ТД частично основываются на диагностических моделях, устанавливающих связь между состояниями ТС и их отображениями в производстве диагностических сигналов. Важной частью проблемы распознавания являются правила принятия решений.

Решение диагностической задачи (отнесение изделия к исправным или несправным) всегда связано с риском ложной тревоги или пропуска цели. Для принятия обоснованного решения целесообразно привлекать методы теории статических решений.

Вторым важным направлением ТД является теория контролеспособности. Контролеспособность - свойство изделия обеспечивать достоверную оценку его ТС и раннее обнаружение неисправностей и отказов. Крупной задачей теории контролеспособности является изучение средств и методов получения диагностической информации.

Структура ТД.

таблица 1.

Техническая диагностика
Теория распознавания	Теория контролеспособности
Алгоритмы распознавания	Правила решений	Диагност. модели	диагност. информация	Контроль состояния	Поиск неиправн

Состояние системы описывается совокупностью (множеством) определяющих ее параметров (признаков). Разумеется, что множество определяющих параметров может быть различным, в первую очередь, в связи с самой задачей распознавания.

Распознавание состояния системы - отнесение состояния системы к одному из возможных классов (диагнозов). Число диагнозов зависит от особенностей задачи и целей исследования.

В большинстве задач ТД диагнозы устанавливают заранее и в этих условиях задачу распознавания часто называют задачей классификации.

Совокупность последовательных действий в процессе распознавания называется алгоритмом распознавания. Существенной частью процесса распознавания явл. выбор параметров, описывающих состояние системы. Они должны быть достаточно информативны, чтобы при выбранном числе диагнозов процесс разделения (распознавания) мог быть осуществлен.

Математические основы ТД.

В задачах диагностики состояния системы часто описывается с помощью комплекса признаков.

,

где 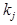- признак, имеющий 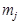разрядов.

В общем случае каждый экземпляр системы соответствует некоторой реализации комплекса признаков

.

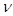Во многих алгоритмах распознавания удобно характеризовать системы параметрами , образующими - мерный вектор или точку в 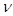- мерном пространстве:

.

Отсюда видно, что принципиальных отличий при описании системы с помощью признаков или параметров нет.

Существует два основных подхода к задаче распознавания: вероятностный и детерменистский. Постановка задачи при вероятностных методах такова. Имеется система, которая находится в одном из случайных состояний 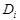. Известна совокупность признаков (параметров), каждый из которых с определенной вероятностью характеризует состояние системы. Требуется построить решающее правило, с помощью которого диагностируемая совокупность признаков была бы отнесена к одному из возможных состояний. Желательно также оценить достоверность принятого решения и степень риска ошибочного решения. При детерменистских методах распознавания удобно формулировать задачу на геометрическом языке. Если система характеризуется 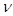- мерным вектором , то любое состояние системы представляет собой точку в 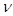- мерном пространстве параметров (признаков). Задача здесь сводится к разделению пространства параметров на области диагнозов. При детерменистском подходе области диагнозов обычно считаются непересекающимися, т.е. вероятность одного диагноза равна единице, вероятность других равна нулю.