Интегрирование некоторых иррациональных функций
Если f(x) = 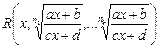 , то для ее интегрирования применяют подстановку
, то для ее интегрирования применяют подстановку 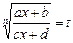 , где п = НОК (n1, …, nk).
, где п = НОК (n1, …, nk).
Пример. 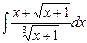 =
= 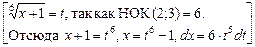 =
=
= 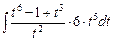 =
=  =
= 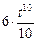 –
– 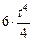 +
+ 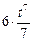 + с =
+ с =
=  –
– 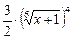 +
+ 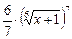 + с =
+ с = 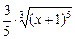 –
–  ·
· 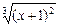 +
+
+ 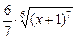 + с.
+ с.
Определенный интеграл и его основные свойства
Пусть на отрезке [a,b] определена функция у = f(x). Разобьем этот отрезок на п частей точками 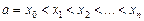 = b. На каждом отрезке [хi–1; xi] возьмем произвольную точку
= b. На каждом отрезке [хi–1; xi] возьмем произвольную точку 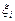 (i = 1, 2,…, п) и составим сумму
(i = 1, 2,…, п) и составим сумму 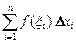 , где
, где 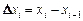 . Сумма
. Сумма 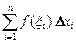 называется интегральной суммой функции f(x) на отрезке [a,b], а ее предел при
называется интегральной суммой функции f(x) на отрезке [a,b], а ее предел при 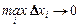 , если он существует и конечен, называется определенным интегралом от функции у = f(x) в пределах от а до b и обозначается следующим образом:
, если он существует и конечен, называется определенным интегралом от функции у = f(x) в пределах от а до b и обозначается следующим образом:
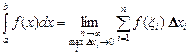 .
.
В этом случае функция у = f(x) называется интегрируемой на отрезке [a,b].
Среди многих экономических интерпретаций определенного интеграла отметим следующую:
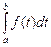 равен объему производства от момента времени t при условии, что f(t) — производительность труда в момент времени t.
равен объему производства от момента времени t при условии, что f(t) — производительность труда в момент времени t.
Определенный интеграл имеет следующие свойства:
1. 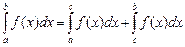 .
.
2. 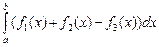 =
= 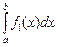 +
+ 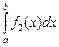 –
– 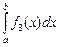 .
.
3. 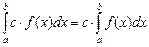 .
.
Формула Ньютона-Лейбница и интегрирование по частям
Если функция у = f(x) непрерывна на отрезке [a,b] и F(x) — одна из первообразных для f(x), то справедлива формула Ньютона-Лейбница
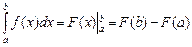 .
.
Если и = и(х), v = v(x) — дифференцируемые функции на отрезке [a,b], то
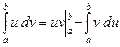 .
.
Замена переменной в определенном интеграле
Если 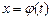 — функция, непрерывная вместе со своей производной
— функция, непрерывная вместе со своей производной 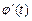 на отрезке [
на отрезке [ 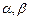 ],
], 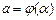 ,
, 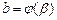 , то
, то
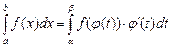 .
.
Вычисление площадей плоских фигур при помощи определенного интеграла
Площадь фигуры, ограниченной кривыми (рис. 18) у = f1(x), у =
= f2(x) (f1(x) 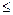 f2(x)) и прямыми х = а, х = b, находится по формуле
f2(x)) и прямыми х = а, х = b, находится по формуле
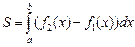 .
.
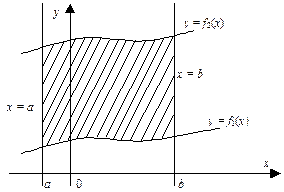 |
| Рис. 18 |
Вопросы для самопроверки
1. Что называется первообразной для функции y = f(x)?
2. Что называется неопределенным интегралом от функции y = f(x)?
3. Какие свойства имеет неопределенный интеграл?
4. Какие методы интегрирования вы знаете?
5. Какие типы простейших рациональных дробей вы знаете? Как они интегрируются?
6. Каким образом находятся неопределенные интегралы от рациональных дробей?
7. Какой вы знаете метод интегрирования иррациональностей?
8. Что называется определенным интегралом?
9. Какие вы знаете свойства определенного интеграла?
10. Какую экономическую интерпретацию определенного интеграла вы знаете?
11. Каким образом применяется определенный интеграл для вычисления площадей плоских фигур?
Типовая задача 2
Найти неопределенные интегралы:
1) 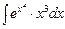 ;
;
2) 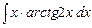 ;
;
3) 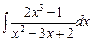 .
.
Результаты проверить дифференцированием.
Решение. 1) Так как 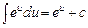 , то, положив u = x4, получим
, то, положив u = x4, получим
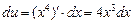 .
.
Отсюда 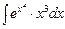 =
= 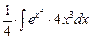 =
= 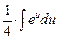 =
= 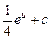 =
=
= 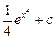 .
.
Проверка: 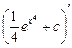 =
= 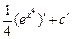 =
= 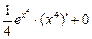 =
=  =
=
= 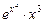 .
.
2) Применим формулу интегрирования по частям:
u = arctg2x  du =
du = 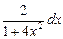 , dv = xdx
, dv = xdx  v =
v = 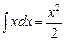 .
.
Тогда 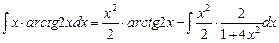 =
= 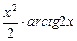 –
–
– 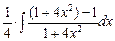 =
= 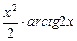 –
– 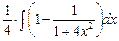 =
= 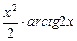 –
–
– 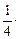
 =
= 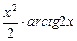 –
– 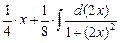 =
= 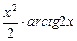 –
–
– 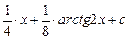 .
.
Проверка: 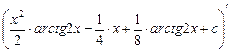 =
= 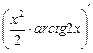 –
–
– 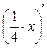 +
+ 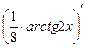 + с' =
+ с' = 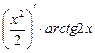 +
+ 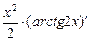 –
– 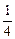 +
+
+ 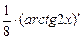 + 0 =
+ 0 = 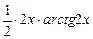 +
+ 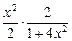 –
– 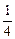 +
+ 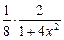 = =
= = 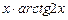 +
+ 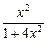 –
– 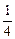 +
+ 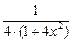 =
= 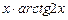 +
+ 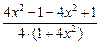 =
=
= 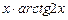 .
.
3) Данная подынтегральная дробь неправильная, поэтому сначала выделим целую часть, поделив числитель на знаменатель:
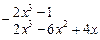 | x2 – 3x + 2 | ||
| 2x + 6 | |||
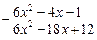 | |||
| 14x – 13 | |||
Итак, 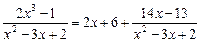 .
.
Отсюда 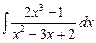 =
= 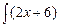 dx +
dx + 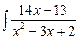 dx = [х2 – 3х + 2 =
dx = [х2 – 3х + 2 =
= (х – 1) · (х – 2)] = 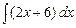 +
+ 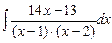 = I .
= I .
Представим правильную дробь в виде суммы простейших:
 =
= 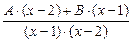 = =
= = 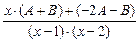 .
.
Избавляясь от знаменателей, получим
14х – 13 = (А + В) · х + (–2А – В).
Приравнивая соответствующие коэффициенты при неизвестных в левой и правой частях равенства, получим систему уравнений
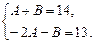

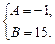
Тогда 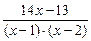 =
= 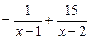 .
.
Итак, 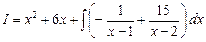 =
= 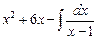 +15·
+15· 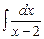 =
=
= 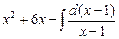 +
+ 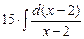 =
= 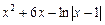 +
+ 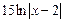 + с.
+ с.
Проверка: 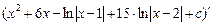 = (х2)' + (6х)' –
= (х2)' + (6х)' –
– (ln |x – 1|)' + (15 · ln|x – 2|)' + c' = 2x + 6 – 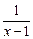 · (x – 1)' +
· (x – 1)' +
+ 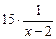 · (x – 2)' + 0 = 2x + 6 –
· (x – 2)' + 0 = 2x + 6 – 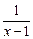 +
+ 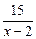 =
=
= 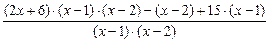 =
=
= 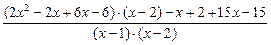 =
=
= 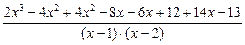 =
= 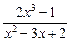 .
.
Ответ: 1) 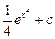 ; 2)
; 2) 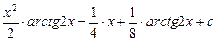 ;
;
3) 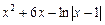 +
+ 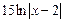 + с.
+ с.
Типовая задача 3
Найти площадь фигуры, заключенной между линиями y = x2 – 7x +
+ 12, y = x – 3.
Решение. Фигура имеет вид, изображенный на рис. 19.
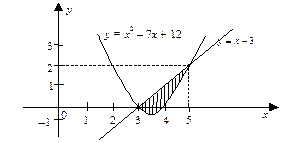 |
| Рис. 19 |
Определим координаты точек пересечения линий. Для этого решим следующую систему уравнений:
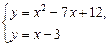

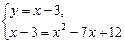

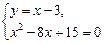


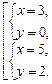
Абсциссы точек пересечения линий — х = 3, х = 5. Следовательно, пределы интегрирования — а = 3, b = 5.
Таким образом, 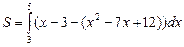 =
= 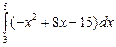 =
=
= 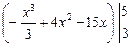 =
= 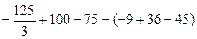 =
= 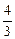 (кв. ед.).
(кв. ед.).
Ответ: 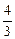 кв. ед.
кв. ед.
3. Задания 4 и 5
по теме «Ряды и их применение
к приближенным вычислениям определенных интегралов»
