ПрактикалыҚ сабаҚ 7. Үш еселік интегралдарда айнымалыларды ауыстыру

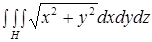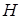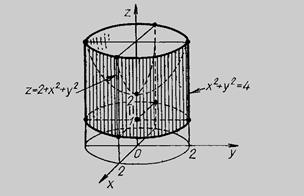
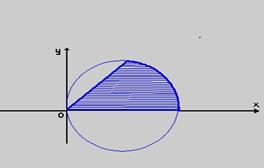
Мысал 2. Интегралды есепте , егер облысы 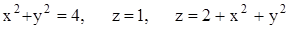беттерімен шенелген болса (сурет-14).

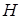облысының шекарасының теңдеулерін (**) цилиндрлік кординатаға көшіріп, 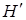облысының шекарасының теңдеулерін жазамыз.

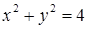-дан 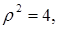аламызғ, яғни .

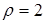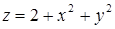теңдеуі поляр координатада 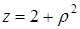өрнектеледі, ал 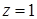өзгермейді. 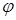және 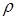айнымалылары үшін, .

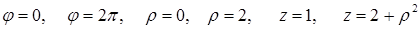Сондықтан, мынаны аламыз

.

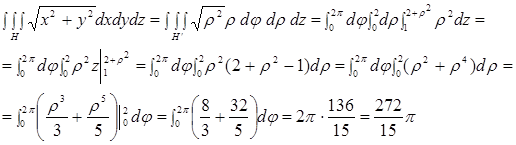Әдебиеттер

Г.Н.Берман. Сборник задач по курсу математического анализа. М., «Наука» - 1977.

Бақылау сұрақтар

1. Кеңістік облычтарды түрлендіру?
2. Көлемнің қисық сызықты координатталар арқылы өрнегі?
3. Цилиндрлік және сфералық координатталар?

Ш еселік интегралдарды қолданулары.

Үш еселік интегралды пайдаланып, 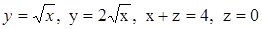беттерімен шектелген дененің көлемін табыңдар.

Шешуі: 6-сурет. Жоғарғы жағынан 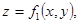төменгі жағынан 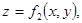үздіксіз беттерімен, ал бүйір жағынан тік цилиндрмен шектелген, және 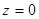жазықтығындағы 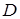облысына проекцияланатын цилиндрін дене 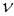–нің көлемі туралы теория бойынша

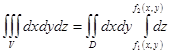
формуласымен табылады.

6(а)-сурет 6(б)-сурет

Бұл дененің жоғары жағынан 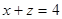беттен, ал төменгі жағынан 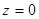жазықтығымен, ал бүйір жағынан 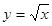және 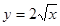тік цилиндрмен шектелген цилиндрдік дене деп қарастырамыз 6(а) сурет. Интегралдау облысы 6(б) сурет.

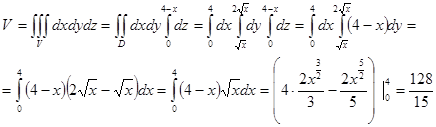
Әдебиеттер

Г.Н.Берман. Сборник задач по курсу математического анализа. М., «Наука» - 1977.

Бақылау сұрақтар

1. Үш еселік интегралдың механикалық қолданулары?
2. Үш еселік интегралдың геометриялық қолданулары?

ПРАКТИКАЛЫҚ САБАҚ 8-11. БІРІНШІ ТИПТІ ҚИСЫҚСЫЗЫҚТЫ ИНТЕГРАЛ ЖӘНЕ ЕКІНШІ ТИПТІ ҚИСЫҚСЫЗЫҚТЫ ИНТЕГРАЛ. ГРИН ФОРМУЛАСЫ.

Пример. Қисық сызықты интегралды есепте 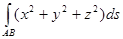по одному витку винтовой линии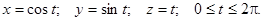

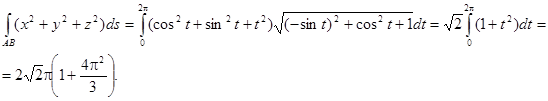
Мысал. 1 типті Қисықсызықты интегралды есепте 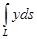, где L- y=2x+1, , мұндағы L – түзу (АВ) А(0.1), В(1, 3)

Шешімі.

(АВ) тұзудің теңдеуді табамыз 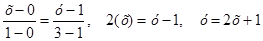Онда 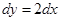, х-тің шектері 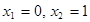Қисықсызықты интегралдан анықталған интегралға көшу

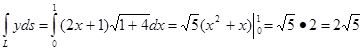
Мысал. 2 ші типтьі Қисықсызықты интегралды есепте 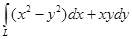,где L- отрезок от А (1,1) до В(3, 4)

Шешімі.

(АВ) тұзудің теңдеуді табамыз 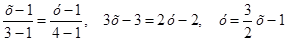Онда 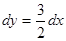, х-тің шектері 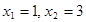Қисықсызықты интегралдан анықталған интегралға көшу

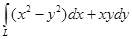
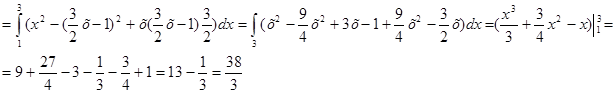
Әдебиеттер

Г.Н.Берман. Сборник задач по курсу математического анализа. М., «Наука» - 1977.

Бақылау сұрақтар

1. Бірінші типті қисық интегралдың анықтамасы?
2. Бірінші типті қисық интегралдың бар болуы шарты?
3. Физикалық есептерге қолдану

ПРАКТИКАЛЫҚ САБАҚ 12-14. БІРІНШІ ЖӘНЕ ЕКІНШІ ТИПТІК БЕТТІК ИНТЕГРАЛДАРЫ

Пример. Вычислить криволинейный интеграл 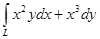. L – контур, ограниченный параболами 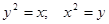. Направление обхода контура положительное.

Представим замкнутый контур L как сумму двух дуг L₁ = x² и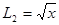

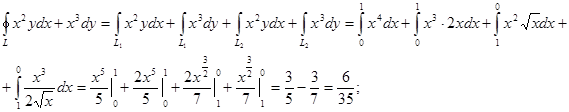
Пример. Решим пример, рассмотренный выше, воспользовавшись формулой Остроградского – Грина.

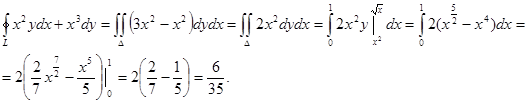
Әдебиеттер

Г.Н.Берман. Сборник задач по курсу математического анализа. М., «Наука» - 1977.

Бақылау сұрақтар