Алгоритм перебора робертса - флореса

( алгоритм поиска гамильтонова цикла ).

Выбирается некоторая начальная вершина графа v₁. Эта вершина образует первый элемент множества S: S = {v₁}. Множество S на каждом шаге будет хранить уже найденные вершины гамильтоновой цепи. К S добавляется первая вершина (пусть это вершина a) в столбце v₁. Затем к S добавляется первая возможная вершина в столбце a. Пусть это вершина b, затем к S добавляется первая возможная вершина (например, с) в столбце b и т.д.

S = { v₁, a, b, с, . . .}

Под «возможной» понимается вершина, которой нет в S.

Пусть множество S на шаге r имеет вид: S = { v₁, a, b, c, …, v_r-1, v_r}.

Существует две причины, препятствующих включению некоторой вершины во множество S.

1. В столбце v_r нет возможной вершины (множество S нельзя расширить).

2. Цепь, определеляемая последовательностью вершин в множестве S, имеет длину p-1, где p – количество вершин графа, т. е. она является гамильтоновой цепью.

Во втором случае тоже 2 варианта:

а) в графе G существует ребро (vr,v₁), следовательно, найден гамильтонов цикл;

б) ребро (vr,v₁) не существует, следовательно, гамильтонов цикл не может быть получен.

В случаях 1) и 2б) следует прибегнуть к возвращению, а в случае 2а) прекратить поиск (если необходимо найти только один гамильтонов цикл) или (если нужны все гамильтоновы циклы) прибегнуть к возвращению. Возвращение состоит в удалении последней включенной вершины из S, после чего множество S примет вид: S = {v₁, a, …, v_r-1} и добавлении к S первой возможной вершины, следующей за vr в столбце v_r-1. Если не существует никакой возможной вершины, то делается следующий шаг возвращения и т. д.

Поиск заканчивается, когда множество S состоит из одной вершины v₁ и не существует никакой возможной вершины, которую можно добавить в S, так что шаг возвращения делает S пустым. Это значит, что все гамильтоновы циклы найдены. Алгоритм заканчивает работу.

Пример:

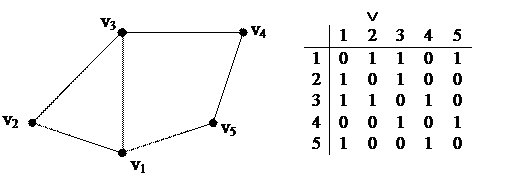“2”

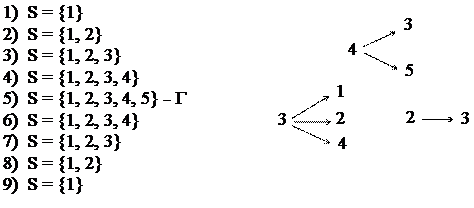“3”

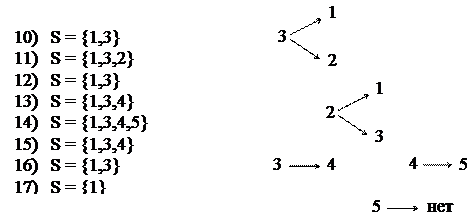“5”

18) S = {1, 5}

19) S = {1, 5, 4}

20) S = {1, 5, 4, 3}

21) S = {1, 5, 4, 3, 2} - Г

22) S = {1, 5, 4, 3}

23) S = {1, 5, 4}

24) S = {1, 5}

25) S = {1}

26) S = Æ

ЗАДАЧА КОММИВОЯЖЕРА И ЗАДАЧА КИТАЙСКОГО ПОЧТАЛЬОНА

Задача коммивояжера- это обобщение задачи о поиске гамильтонова цикла в графе.

Постановка задачи. В полном взвешенном графе G построить маршрут (цикл, цепь) минимального веса, проходящий по крайней мере один раз через каждую вершину исходного графа.

Если такой маршрут существует, то задача сводится к задаче поиска гамильтонова цикла.

Задача китайского почтальона - это обобщение задачи о поиске эйлерового цикла в графе.

Постановка задачи. Построить маршрут (цикл, цепь) с минимальным суммарным весом, проходящий по каждому ребру графа.

ОСНОВЫ ЦИКЛОМАТИКИ

Рассмотрим (p,q)-граф, имеющий k компонент связности.

Число 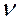(G) = q – p + k называется цикломатическим числом, илициклическим рангом; число 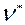(G) = p – k называется коциклическим рангом.

Теорема. Количество ребер остова (ветвей) произвольного графа G равно его коциклическому рангу, а количество ребер, которые необходимо удалить для построения остова (хорд), равно его циклическому рангу.

Каждому циклу графа ставится в соответствии вектор длиной q, где q – количество ребер графа G.

z_c = (z₁,z₂,…,z_q), где

z_i =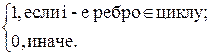

Пример:

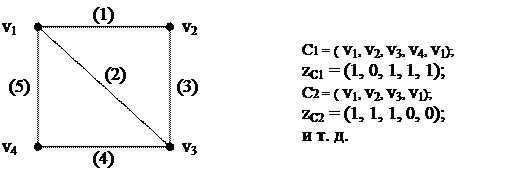
Множество всех векторов, каждый из которых соответствует одному циклу графа G, образует векторное пространство, которое называется пространством циклов графа G.

Пусть z, 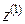, …, 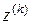- некоторые вектора пространства, тогда если

z = 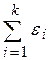* 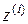, где 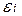Î {0, 1}, а 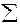- есть операция сложения по mod 2,

то вектор z - линейная комбинация векторов , …, .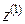

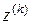Векторы z₁, z₂, …, z_k называются линейно независимыми, если никакой вектор этого множества не может быть представлен в виде линейной комбинации остальных.

Векторы z₁, z₂, …, z_k образуют базис в векторном пространстве, если:

1) они линейно независимы;

2) любой вектор этого пространства можно представить в виде линейной комбинации остальных векторов.

Циклы, соответствующие базисным векторам, образуют базис циклаграфа G и называются базисными, или фундаментальными.

Теорема Эйлера. Число базисных векторов (циклов) постоянно и равно его цикломатическому числу (циклическому рангу):

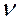(G) = q – p + k.

Следствие 1. Если 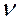(G) = 0, то граф G является ациклическим.

Следствие 2.Если 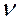(G) = 1, то граф содержит один единственный простой цикл.

Следствие 3. 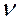(G) ³ 0.

Базисной системой циклов G называется множество всех циклов графа, каждый из которых содержит ровно одну хорду для произвольного заданного остова T. Эта система векторов образует базис, поскольку каждый из этих циклов содержит ребро (хорду), не принадлежащее ни одному из остальных циклов, следовательно, они линейно независимы, и все остальные циклы могут быть выражены в виде линейной комбинации этих циклов.