Курс бойынша емтихан сұрақтары. 1. Анықтауыштың қандай қасиеттері бар?
1. Анықтауыштың қандай қасиеттері бар?
2. Матрица дегеніміз не? Оған қандай элементар түрлендірулер жасауға болады?
3. Алгебралық толықтауыш және минор дегеніміз не?
4. Матрицаларға қандай амалдар қолданылады?
5. Матрица рангісі қандай әдістермен табылады?
6. Кез келген матрицаның керісі бола ма?
7. Сызықты алгебралық теңдеулер жүйесін шешудің қандай әдістері бар?
8. Қандай жағдайда біртекті сызықты алгебралық теңдеулер жүйесінің нөлдік емес шешімдері болады?
9. Кронекер-Капелли теоремасын тұжырымдаңыз.
11. Крамер формуласын жазыңыз. Ол қандай жағдайда қолданылады?
12. Вектор дегеніміз не? Оның координаттары, модулі қалай анықталады?
13. Вектордың бағыттауыш косинустары дегеніміз не?
14. Сызықты тәуелді немесе сызықтық тәуелсіз векторлар дегеніміз не?
15. Векторлардың коллинеарлық, компланарлық, теңдік шарттары қандай?
16. Координаттық түрде берілген векторларға сызықтық амалдар қалай қолданылады?
17. Жазықтықтағы түзу қалай анықталады?
18. Екі түзудің параллельдік, перпендикулярлық шарттары қандай?
19. Түзудің 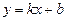 теңдеуіндегі
теңдеуіндегі 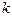 коэффициентінің мағынасы қандай?
коэффициентінің мағынасы қандай?
20. Кеңістіктегі түзудің бағыттауыш векторы дегеніміз не?
21. Жазықтықтың жалпы теңдеуін жазыңыз. Ондағы коэффициенттер нені білдіреді?
22. Нүктеден жазықтыққа дейінгі қашықтықты қалай есептейді?
23. Екі түзу немесе екі жазықтық, түзу мен жазықтық арасындағы бұрыштар қандай векторлармен анықталады?
24. Кеңістіктегі түзудің жалпы теңдеуі қалай анықталады?
25. Екінші ретті қисықтарға ортақ қасиеті қандай?
26. Екінші ретті беттердің қандай түрлері бар?
27. Екінші ретті қисықтың эксцентриситеті нені сипаттайды?
28. Екінші ретті қисықтардың фокустары қалай анықталады?
29. Цилиндрлік беттердің қандай түрлері бар?
30. Айналу беттерінің қандай түрлері бар?
31. Функцияның негізгі сипаттамалары қандай?
32. Тізбек дегеніміз не? Жинақты тізбек дегеніміз не?
33. Функцияның шегі туралы негізгі теоремалар қандай?
34. Тақ, жұп функциялар қалай анықталады?
35. Қандай тізбектің шегі 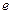 санына тең?
санына тең?
36. Қандай тамаша шектер бар?
37. Шексіз аз, шексіз үлкен шамалар дегеніміз не?
38. Функцияны үзіліссіздікке қалай зерттейді?
39. Үзіліс нүктелерінің қандай түрлері бар?
40. Кесіндіде үзіліссіз функцияның негізгі қасиеттері қандай?
41. Шексіз аз шамалардың қандай қасиеттерін білесіз?
42. Функцияның біржақты шектері дегеніміз не?
43. Бірінші және екінші текті үзілісті функцияларды қалай ажыратуға болады?
44. Функция кесіндіде үзіліссіз болса, онда оны шектелген функция деуге бола ма?
45. Функция туындысының геометриялық және физикалық мағыналары қандай?
46. Функция дифференциалы дегеніміз не?
47. Негізгі дифференциалдау ережелері қандай?
48. Логарифмдік дифференциалдау әдісі қандай жағдайларда қолданылады?
49. Күрделі, кері, айқындалмаған функциялардың туындылары қалай табылады?
50. Ролль теоремасын тұжырымдаңыз. Оның геометриялық мағынасы қандай?
51. Лагранж теоремасын тұжырымдаңыз. Оның геометриялық мағынасы қандай?
52. Лопиталь ережелері не үшін қолданылады?
53. Тейлор, Маклорен формулалары не үшін қолданылады?
54. Функцияның иілу нүктесін қалай анықтайды?
55.Күдікті нүктелерді қалай анықтайды?
56. Функцияның өсуі мен кемуінің белгілері қандай?
57. Функцияның экстремумының бар болуының қажетті, жеткілікті шарттары қандай?
58. Функцияның ойыс, дөңес болуының шарттары қандай?
59. Кесіндіде дифференциалданатын функцияның ең үлкен, ең кіші мәндері қалай табылады? Барлық жағдайда да олар бар бола ма?
60. Анықталмаған интегралдың анықтамасын тұжырымдаңыз.
61. Анықталмаған интегралдың негізгі қасиеттері қандай?
62. Анықталған интегралды қандай формуламен есептейді?
63. Анықталған интегралдың қасиеттері қандай?
64. Меншіксіз интегралдың жинақтылық белгілері қандай?
65. Анықталған интегралды есептеудің қандай әдістерін білесіз?
66. Жазық фигураның ауданын қалай есептейді?
67. Қисық доғасының ұзындығын қалай есептейді?
68. Айналу денесінің көлемін көлденең қимасының ауданы арқылы қалай есептейді?
69. Жазық фигураның ауданын қалай есептейді?
70. Қисық доғасының ұзындығын қалай есептейді?
71. Вектордың орты.
72. Коллинеар векторлар.
73. Компланар векторлар.
74. Векторларға қолданылатын сызықтық амалдар.
75. Векторлардың коллинеарлығының қажетті және жеткілікті шарттары.
76. Сызықтық тәуелді және тәуелсіз векторлар.
77. Векторды координат өстердің орттары арқылы жіктеу.
78. Вектордың модулі.
79. Вектордың бағыттаушы косинустары.
80. Координаттарымен берілген векторларға амалдар қолдану.
81. Кесіндіні берілген қатынаста бөлу формулалары.
82. Кесіндінің ортасын табу формуласы.
83. Векторлардың скалярлық көбейтіндісі.
84. Векторлардың векторлық көбейтіндісі.
85. Векторлардың аралас көбейтіндісі.
86. Жазықтықтағы түзулердің әртүрлі теңдеулері.
87. Түзулердің арасындағы бұрыш.
88. Екі түзудің параллельдік және перпендикулярлық шарттары.
89. Нүктеден түзуге дейінгі қашықтық.
80. Жазықтықтың әртүрлі теңдеулері.
81. Екі жазықтықтың арасындағы бұрыш.
82. Екі жазықтықтың параллельдік және перпендикулярлық шарттары.
83. Нүктеден жазықтыққа дейінгі қашықтық.
84. Кеңістіктегі түзудің әртүрлі теңдеулері.
85. Түзу мен жазықтықтың өзара орналасуы.
86. Эллипстің канондық теңдеуі.
87. Гиперболаның канондық теңдеуі.
88. Параболаның канондық теңдеуі.
89. Екінші ретті беттердің канондық теңдеулері.
90. Функцияның анықтамасы.
91. Аралықта өсетін және кемитін функциялар.
92. Жұп және тақ функциялар.
93. Периодты функциялар.
94. Күрделі функция.
95. Кері функция.
Арнайы бөлмелер мен зертханалар тізімі
Дәріс сабақтарын жүргізуге арналған № 22-62 (2- оқу корпусы) аудиториялар бар (мультимедиялық кешенді)
Глоссарий
| №№ | Жаңа ұғымдар | Мағынасы |
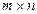 өлшемді матрица өлшемді матрица | 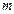 жатық және жатық және 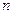 тік жолдардан құралған сандардың тікбұрышты кестесі тік жолдардан құралған сандардың тікбұрышты кестесі | |
| Матрица анықтауышы | Әрбір квадрат матрицаға белгілі бір ереже бойынша қойылған сан. 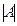 символымен белгілейді символымен белгілейді | |
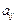 элементінің миноры элементінің миноры | Анықтауыштың 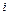 - жатық, - жатық, 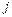 - тік жолдарын сызып тастағанда шығатын анықтауыш. - тік жолдарын сызып тастағанда шығатын анықтауыш. 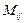 - символымен белгілейді. - символымен белгілейді. | |
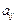 элементінің алгебралық толықтауышы элементінің алгебралық толықтауышы | 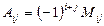 , яғни «+» немесе «-» таңбасымен алынған осы элементтің миноры , яғни «+» немесе «-» таңбасымен алынған осы элементтің миноры | |
| Кері матрица | 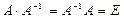 , мұндағы Е-бірлік матрица, теңдіктерін қанағаттандыратын , мұндағы Е-бірлік матрица, теңдіктерін қанағаттандыратын 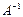 матрицасы матрицасы | |
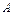 матрицасының рангісі матрицасының рангісі | Матрицаның нөлге тең емес минорларының ең үлкен реті немесе оның сызықты тәуелсіз жатық немесе тік жолдарының саны, 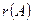 немесе немесе 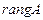 символымен белгілейді. символымен белгілейді. | |
| Базистік минор | Реті рангіні анықтайтын минор | |
| Жолдардың сызықты комбинациясы | 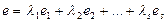 , , 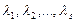 - кез келген сандар - кез келген сандар | |
| Жолдардың сызықты тәуелділігі | Егер бәрі бірдей нөлге тең емес 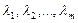 нақты сандары табылып, нақты сандары табылып, 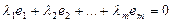 теңдігі орындалатын теңдігі орындалатын 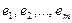 жолдары сызықты тәуелді деп аталады, жолдары сызықты тәуелді деп аталады, 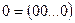 . . | |
| Жолдардың сызықты тәуелсіздігі | 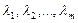 нақты сандарының тек қана нөлдік мәндері үшін нақты сандарының тек қана нөлдік мәндері үшін 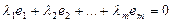 теңдігі орындалатын теңдігі орындалатын 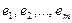 жолдары сызықты тәуелсіз деп аталады. жолдары сызықты тәуелсіз деп аталады. | |
| Кеңейтілген матрица | Жүйенің коэффициенттерінен құрылған негізгі матрицаға бос мүшелердің тік жолы қосылған матрица | |
| Іргелі шешімдер жүйесі | Жүйенің барлық сызықты тәуелсіз шешімдер жүйесі | |
| Векторлардың сызықты комбинациясы | 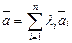 формуласымен анықталатын формуласымен анықталатын 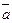 векторы, векторы, 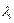 - нақты сандар. - нақты сандар. | |
| Сызықты тәуелсіз векторлар | 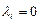 болғанда болғанда 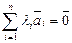 теңдігі орындалатын теңдігі орындалатын 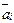 векторлары векторлары | |
| Сызықты тәуелді векторлар | 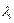 сандарының кем дегенде біреуі нөлге тең емес болғанда сандарының кем дегенде біреуі нөлге тең емес болғанда 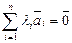 теңдігі орындалатын теңдігі орындалатын 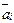 векторлары векторлары | |
| Базистік векторлар | 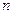 сызықты тәуелсіз векторлар жиынтығы сызықты тәуелсіз векторлар жиынтығы | |
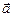 векторының бағыттаушы косинустары векторының бағыттаушы косинустары | 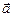 векторының декарт координат өстерімен жасайтын сәйкес векторының декарт координат өстерімен жасайтын сәйкес 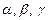 - бұрыштарының косинустары - бұрыштарының косинустары | |
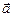 векторының орты векторының орты | 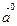 =( =( 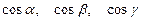 ) , бағыты ) , бағыты 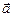 векторымен бағыттас және осы вектордың бойында жатқан бірлік вектор векторымен бағыттас және осы вектордың бойында жатқан бірлік вектор | |
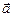 , , 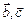 векторларының оң және сол жүйелері векторларының оң және сол жүйелері | Егер 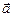 векторынан векторынан 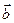 векторына қарай бұрылу векторына қарай бұрылу 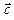 векторының ұшынан қарағанда сағат тілінің қозғалу бағытына қарсы болатын жүйені оң жүйе, ал – бағыттас болса, сол жүйе деп атайды. векторының ұшынан қарағанда сағат тілінің қозғалу бағытына қарсы болатын жүйені оң жүйе, ал – бағыттас болса, сол жүйе деп атайды. | |
| Нормаль вектор | Жазықтықтағы түзуге немесе жазықтыққа перпендикуляр болатын вектор | |
| Бағыттаушы вектор | Кеңістіктегі түзу бойындағы немесе оған параллель болатын нөлдік емес вектор | |
| Эксцентриситет | 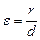 , екінші ретті қисықтың бойындағы кез келген нүктесінің берілген нүкте (фокус) мен берілген түзуден (директриса) қашықтықтарының қатынасы , екінші ретті қисықтың бойындағы кез келген нүктесінің берілген нүкте (фокус) мен берілген түзуден (директриса) қашықтықтарының қатынасы | |
| Фокальдық радиус | Екінші ретті қисықтың бойындағы кез келген нүктені фокуспен қосатын кесінді | |
| Парабола параметрі | Фокустан директрисаға дейінгі қашықтық, 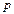 деп белгіленеді деп белгіленеді | |
| Түйіндес гиперболалар | Асимптоталары бірдей болатын гиперболалар | |
| Эллипс (гипербола) директрисалары | Эллипстің үлкен өсіне (гиперболаның нақты өсіне) перпендикуляр болып, центрінен бірдей 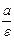 қашықтықта орналасатын екі түзу қашықтықта орналасатын екі түзу | |
| Сызықтық бет | Жасаушылары түзулерден тұратын бет | |
| Шексіз аз шама | 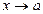 болғанда шектері нөлге ұмтылатын айнымалы шама болғанда шектері нөлге ұмтылатын айнымалы шама | |
| Шексіз үлкен шама | 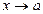 болғанда шектері шексіздікке тең болатын айнымалы шама болғанда шектері шексіздікке тең болатын айнымалы шама | |
| Шек пен шексіз аз шама арасындағы байланыс | 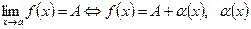 - шексіз аз шама - шексіз аз шама | |
| Аргумент өсімшесі | 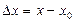 айырымын айырымын 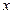 аргументінің аргументінің 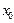 нүктесіндегі өсімшесі дейді нүктесіндегі өсімшесі дейді | |
Функцияның 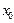 нүктедегі өсімшесі нүктедегі өсімшесі | 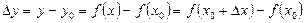 айырымы айырымы | |
| Күрделі функция туындысы | 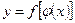 , , 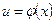 . . 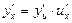 | |
Функцияның 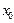 нүктедегі туындысы нүктедегі туындысы | 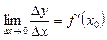 | |
| Функция дифференциалы | Функция өсімшесінің басты бөлігі. 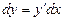 | |
Функцияның 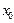 нүктедегі үзіліссіздігі нүктедегі үзіліссіздігі | 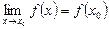 теңдігінің орындалуы теңдігінің орындалуы | |
| Алғашқы функция | 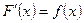 теңдігі орындалатын теңдігі орындалатын 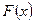 функциясы функциясы 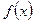 функциясының алғашқы функциясы болады функциясының алғашқы функциясы болады | |
| Анықталмаған интеграл | 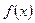 функциясының функциясының 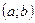 аралығындағы барлық алғашқы функцияларының жиынтығы - аралығындағы барлық алғашқы функцияларының жиынтығы - 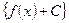 | |
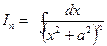 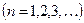 , интегралының рекурентті формуласы , интегралының рекурентті формуласы | 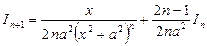 | |
| Анықталған интеграл | 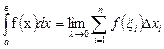 | |
| Ньютон-Лейбниц формуласы | 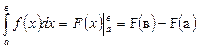 , мұндағы , мұндағы 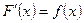 | |
| Меншіксіз интеграл | Ақырсыз шекті (шектері шексіздік болып келген) және шенелмеген (үзілісті) функциялардың интегралдары | |
| 1-текті меншіксіз интеграл | Ақырсыз шекті функциялардың интегралдары: а) 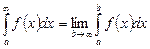 б) б) 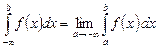 ; в) ; в) 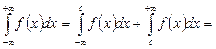 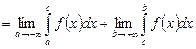 | |
| 2-текті меншіксіз интеграл | Шенелмеген (үзілісті) функциялардың интегралдары: а) 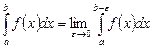 б) б) 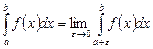 в) в) 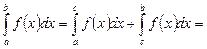 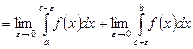 |
