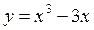Теоретичні відомості про диференціал функції

Головну, лінійно залежну від Δх, частину приросту Δy функції y=f(x), тобто величину 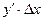, називають диференціалом функції і назначають dy або d(f(x)). Отже, .

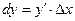Диференціал аргументу дорівнює його приросту dх= Δх. Тому .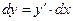

Отже, щоб знайти диференціал функції y=f(x), слід знайти похідну 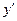цієї функції і помножити цю похідну на диференціал аргументу dx.

Диференціал використовують для наближених обчислень:

1. Для дуже малих значень Δх 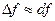, тобто .

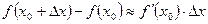2. Для знаходження наближених значень функцій використовують формулу:

.

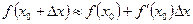Задача № 1. Обчислити диференціал функції 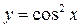при x=π/4 і dx=0,03.

Задача № 2. Знайти наближене значення приросту функції 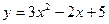в точці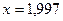

Задача № 3.

а) Обчислити наближене значення функції 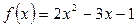при x=2,01

б) Знайти наближене значення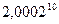

в) Знайти наближене значення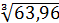

Питання для самоконтролю знань, умінь

1. Похідна суми, добутку, частки двох функцій.

2. Похідна складеної функції.

3. Похідна степеневої функції.

4. Похідні логарифмічної, показникової та тригонометричних функцій.

5. Що називається диференціалом ?

6. Геометричний зміст диференціала

7. Як за допомогою диференціала можна знайти наближене значення приросту функції ?

8. Як обчислити наближене значення функції за допомогою диференціала ?

Висновок__________________________________________________

Перевірив викладач ___________ Оцінка ___________ Дата___________

Виконаємо самостійно

В -1 В -2

1.Знайти наближене значення приросту функції:

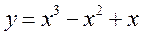
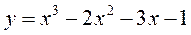
при 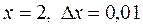при

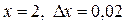
2. Знайти наближене значення функції: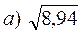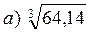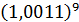

б) б)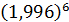

В -3 В - 4

1. Знайти наближене значення приросту функції:

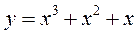
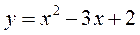
при 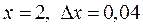при

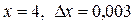
2. Знайти наближене значення функції: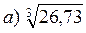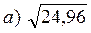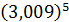

б) б)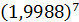

В -5 В -

2. Знайти наближене значення приросту функції:

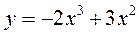
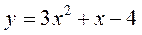
при 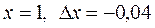при

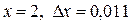
2. Знайти наближене значення функції: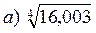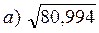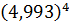

б) б)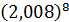

ПРАКТИЧНА РОБОТА № 9

Тема. Схема дослідження і побудови графіка функції за допомогою похідної

Мета роботи: навчитись проводити дослідження функції та будувати її графік.

Наочне забезпечення та обладнання:

1. Інструкційні картки;

2. Приклади задач;

3. Роздаткові матеріали: опорні конспекти “ Основні формули диференціювання ”

4. Обчислювальні засоби: калькулятор.

Теоретичні відомості. Загальна схема дослідження і побудови графіка функції. Алгоритм дослідження функції та побудови графіка

1. Область визначення функції, точки перетину з вісями координат.

2. Дослідження функції на парність, непарність.

3. Знаходження асимптот графіка функції.

Означення. Пряма y= kx+b, де 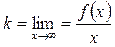, , 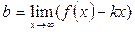називається похилою асимптотою кривої y=f(x).

4. Дослідження функції на монотонність, екстремум.

5. Дослідження на опуклість (вгнутість) та точки перегину графіка функції.

6. Побудова графіка функції

Задача №1. Дослідити та побудувати графік функції