Теоретико-множинні операції з нечіткими множинами.
Так само як для чітких множин можна визначити включення і рівність нечітких множин, а також операції об'єднання, перетинання, доповнення, і т.д. над нечіткими множинами, тільки робиться це за допомогою функції належності.
Нагадаємо, що ступінь належності 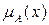 є числами із множини
є числами із множини 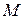 , яка звичайно розглядається як відрізок
, яка звичайно розглядається як відрізок 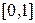 . Введемо деякі операції з ступінями належності, які за позначенням співпадають з операціями алгебри логіки, але в теорії нечітких множин мають інші значення.
. Введемо деякі операції з ступінями належності, які за позначенням співпадають з операціями алгебри логіки, але в теорії нечітких множин мають інші значення.
Означення 2.15. Нехай є два ступеню належності 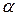 і
і  . Тоді
. Тоді
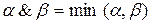 ,
,  ;
;
 ,
, 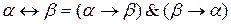 .
.
Тобто нечітка кон’юнкція двох чисел 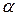 і
і  дорівнює мінімальному з цих двох чисел, а нечітка диз’юнкція дорівнює максимальному з цих двох чисел. Нечітка імплікація визначається більш складно за допомогою нечіткої кон’юнкції, а нечітка еквівалентність за допомогою нечіткої імплікації і кон’юнкції.
дорівнює мінімальному з цих двох чисел, а нечітка диз’юнкція дорівнює максимальному з цих двох чисел. Нечітка імплікація визначається більш складно за допомогою нечіткої кон’юнкції, а нечітка еквівалентність за допомогою нечіткої імплікації і кон’юнкції.
Нехай задані нечіткі підмножини 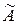 ,
, 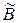 множини
множини 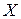 .
.
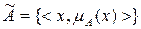 ,
, 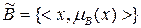 ,
, 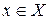 .
.
Означення 2.16. Об'єднанням нечітких множин  є нечітка множина
є нечітка множина 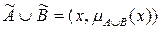 ,
, 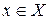 , ступінь належності елементів до якої визначається як
, ступінь належності елементів до якої визначається як  .
.
На рис.2.13 наведений результат виконання операції об’єднання двох нечітких множин, для яких множина 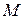 неперервно розподілена на відрізку
неперервно розподілена на відрізку 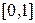 .
.
 |  |
| Рис.2.13 | Рис.2.14 |
Означення 2.17. Перетином двох нечітких множин 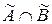 називається нечітка множина
називається нечітка множина 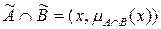 ,
, 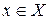 , функція приналежності елементів до якого визначається як
, функція приналежності елементів до якого визначається як  .
.
На рис.2.14 наведений результат виконання операції перерізу двох нечітких множин, для яких множина 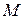 неперервно розподілена на відрізку
неперервно розподілена на відрізку 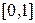 .
.
Тобто 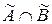 - це нечітка множина, така, що
- це нечітка множина, така, що  і
і  .
.
Означення 2.18. Доповненням нечіткої множини 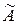 називається нечітка множина
називається нечітка множина  ,
, 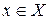 , таке, що
, таке, що 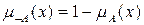 ,
, 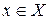 .
.
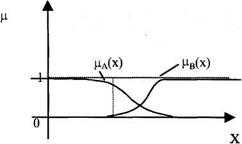
Рис.2.15
Приклад 2.18. Розглянемо нечітку множину 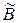 , чисел, набагато більших нуля. Доповненням до цієї множини буде множина
, чисел, набагато більших нуля. Доповненням до цієї множини буде множина 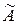 , чисел, набагато менших нуля.
, чисел, набагато менших нуля.
Означення 2.19. Різницею нечітких множин називається множина  ,
, 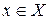 , ступінь належності елементів до якої визначається як
, ступінь належності елементів до якої визначається як  (див. рис.2.15).
(див. рис.2.15).
Означення 2.20. Симетричною різницею  називається множина
називається множина  , де
, де 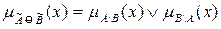 .
.
Приклад 2.19. Нехай є дві нечіткі множини. Найдемо результати виконання визначених операцій:
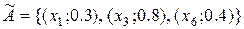 ,
, 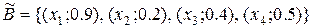 ;
;
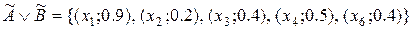 ;
;
 ;
;
 ;
;
 ;
;
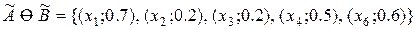 .
.
Означення 2.21. Множиною рівня 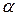 нечіткої множини
нечіткої множини 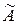 в
в 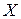 , називається множина у звичному вигляді, складена з елементів
, називається множина у звичному вигляді, складена з елементів 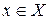 , ступені приналежності яких нечіткій множині
, ступені приналежності яких нечіткій множині 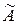 більші або рівні
більші або рівні 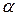 .
.
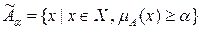 .
.
Нечіткі лінгвістичні змінні. Подальшим узагальненням поняття нечіткої множини є поняття лінгвістичної змінної.
Означення 2.22. Лінгвістичною змінною називається кортеж 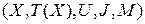
де 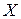 – назва (ім’я) змінної;
– назва (ім’я) змінної;  (або просто
(або просто 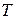 ) – базова множина змінної
) – базова множина змінної 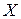 , тобто множина назв лінгвістичних значень змінної
, тобто множина назв лінгвістичних значень змінної 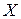 зі значеннями з універсальної множини
зі значеннями з універсальної множини 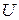 ;
; 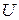 – універсальна множина;
– універсальна множина;  – синтаксичне правило (що має форму граматики), яке породжує назву
– синтаксичне правило (що має форму граматики), яке породжує назву 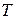 значень змінної
значень змінної 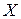 ;
; 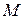 – семантичне правило, що ставить у відповідність кожній нечіткій змінній
– семантичне правило, що ставить у відповідність кожній нечіткій змінній 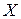 її значення
її значення 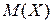 , тобто нечітку підмножину
, тобто нечітку підмножину 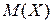 універсальної множини
універсальної множини 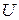 .
.
Конкретна назва 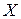 , породжена синтаксичним правилом, називається термом. Терм, що складається з одного або кількох слів, які завжди фігурують разом, називають атомарним. Терм, що складається з одного або більше атомарних термів, називається складним.
, породжена синтаксичним правилом, називається термом. Терм, що складається з одного або кількох слів, які завжди фігурують разом, називають атомарним. Терм, що складається з одного або більше атомарних термів, називається складним.
Пояснимо поняття лінгвістичної змінної на конкретному прикладі.
Приклад 2.19. Нехай експерту треба оцінити вартість випуску продукції за допомогою понять «мала», «середня» і «висока». Максимальна вартість продукції становить 5000 грн. Для формалізації цього опису використовуємо поняття лінгвістичної змінної
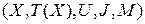 ,
,
де 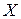 – вартість (назва змінної);
– вартість (назва змінної); 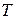 – базова терм-множина, що складається з множини назв лінгвістичних значень змінної
– базова терм-множина, що складається з множини назв лінгвістичних значень змінної 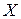 ; тут
; тут 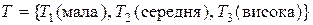 ;
; 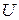 – універсальна множина, тут від 0 до 5000 грн.;
– універсальна множина, тут від 0 до 5000 грн.;  – процедура перебору елементів множини
– процедура перебору елементів множини 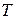 (мала, середня, висока);
(мала, середня, висока); 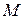 – процедура експертного опиту.
– процедура експертного опиту.
На рис.2.16. показано функції належності відповідних нечітких змінних 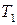 ,
, 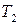 ,
,  .
.
Існує кілька основних аспектів поняття лінгвістичної змінної, які потребують уточнення. По-перше, важливо зрозуміти, що поняття функції належності відмінне від поняття ймовірності. Так, висловлення про те, що значення функції належності «середня вартість» дорівнює 0,5, не має ніякого відношення до ймовірності того, що значення змінної «вартість» дорівнює 2500 грн.
Правильна інтерпретація значення функції належності, яке дорівнює 0,5, полягає в тому, що воно є лише суб’єктивною мірою того, наскільки вартість суми 2500 грн. відповідає в поданні суб’єкта слову «середня». Математичні операції, які застосовуються до значень функції належності, відмінні від операцій, що застосовуються до значень ймовірностей, хоча між ними існує деяка аналогія.
По-друге, лінгвістична змінна має структуру в тому значенні, що вона пов’язана двома правилами:
- синтаксичним – визначає спосіб породження лінгвістичних значень, які належать терму – множині цієї змінної;
- семантичним – визначає спосіб обчислення значень лінгвістичної змінної.

Рис.2.16
Зазначимо у зв’язку з цим, що типове значення лінгвістичної змінної, наприклад «не дуже мала вартість» і «не дуже висока вартість», включає те, що можна було б назвати первинними термами, наприклад «мала» та «середня», значення яких суб’єктивне і залежить від контексту. Передбачається, що значення таких термів визначено заздалегідь.
Дамо означення понять «синтаксичне» та «семантичне» правила.
Синтаксичне правило (процедура) – опис процесу утворення нових, осмислених для певної задачі управління, значень лінгвістичної змінної, виходячи з її терму – множини.
Семантичне правило (процедура) – процес, що дає змогу перетворити кожне нове значення лінгвістичної змінної, яка утворюється синтаксичною процедурою, на нечітку змінну, тобто приписати йому деяку семантику формуванням відповідної нечіткої множини.
