F(x) – некот. первообразная для f(x)
Ф(х) = ∫ f(t)dt также первообразная.
Ф'(x) = f(x), но две любые первообразные отличаются на постоянные согласные т.е. ∫ f(t)dt = F(x) + C
1 Положим х=а, тогда С
1 = F(a)
Cлед-но ∫ f(x)dx = F(x) - F(a)
Положим x=b, тогда ∫ f(t)dt = F(b) - F(a)
Что и требовалось доказать
Ф-ла служит для вычисления
Замена переменной или способ подстановки.
Пусть мы не можем сразу найти первообр-ю для подыинт. выр-я. Сделаем замену перем. х=t по ф-ле х=j(t), где j(t) – непрер. и дифф. ф-я на отрезке [a;b] причем j(a)=a, j(β)=b . Тогда имеет место след. рав-во:
∫ f(x)dx = ∫ f[φ(t)] * φ'(t) dt, здесь φ'(t) dt = dx
Док-во.
Пусть F(x) – первообр. для ф-и f(x). Тогда можно записать:
∫ f(x)dx = F(x) + C
∫ f[φ(t)] * φ'(t) dt = F[φ(t)] + C
а также
∫ f(x)dx =F(x) │= F(b)-F(a), ∫ f[φ(t)]*φ'(t)dt =F[φ(t)] │= F[j(β)] - F[j(a)]=F(b) - F(a)
Пр. часть 2-х посл. рав-в равны, значит, равны и левые. Что и требовалось доказать. Особенностью этой ф-лы явл то, что одновременно с заменой подыинт. выр-я заменяется соответ. образом и пределы инт-я.
Интегрирование по частям.
Рассмотрим рав-во. (u*v)' = u'v + v'u , где v,u - непрерывные фун-ии.
Проинтегрируем по х от a до b:
∫ (u*v)dx = ∫ u'v dx + ∫ uv' dx
т.к. ∫ (u*v)'dx = uv + C , то ∫ (u*v)'dx = uv │ , то получим
∫ u dv = uv│ - ∫ v du , здесь du = u' dx
Вычисление площади плоской фигуры.
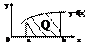 Пусть на отрезке [a;b] ф-я y = f(x) неотрицательна.
Пусть на отрезке [a;b] ф-я y = f(x) неотрицательна.
Тогда Sкрив. трап., огран. этой кривой, осью
ОХ и прямыми х=а, х=b.
Q = ∫ f(x)dx
Если f(x)≤0, то -Q = ∫ f(x)dx , Q = - ∫ f(x)dx
Если ф-я - конечное число раз меняет знак на отр. [a;b], то инт-л по всему отр. разбиваем на сумму инт-лов по частичн. отрезкам. Он будет больше там, где
f(x) >0, и меньше там, где f(x)<0.
Для того, чтобы получить сумму площадей, надо найти или вычислить интеграл
Q = ∫ │f(x)│dx
Если же требуется найти фигуры, ограничен. кривыми y = f
1(x) и y=f
2(x), причем f
1(x) £ f
2(x) на отрезке [a;b], то
Q = ∫ [ f2(x) - f1(x) ]dx
Замечание.
При вычислении площадей следует польз-ся след. св-м интеграла. Интеграл от четной ф-и по симм. пределам равен
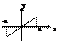 двум интегралам. ∫ f(x)dx =2 ∫ f(x)dx, Q=2 ∫ xdx
двум интегралам. ∫ f(x)dx =2 ∫ f(x)dx, Q=2 ∫ xdx
 Пусть теперь кривая, огран. площадь,
Пусть теперь кривая, огран. площадь,
 задана параметрически, т.е. в виде y = ψ(t), где α ≤ t ≤ β
задана параметрически, т.е. в виде y = ψ(t), где α ≤ t ≤ β
a = φ(α), b = φ(β) x = φ(t)
Пусть это ур-е опред. некотр. ф-ю. y=f(x).
Чтобы опред. эту кривую, надо искл. t.
Сделаем замену перем. Q = ∫ y dx Q = ∫ ψ(t) * ψ'(t) dt
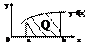 Пусть на отрезке [a;b] ф-я y = f(x) неотрицательна.
Пусть на отрезке [a;b] ф-я y = f(x) неотрицательна.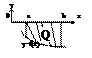
 двум интегралам. ∫ f(x)dx =2 ∫ f(x)dx, Q=2 ∫ xdx
двум интегралам. ∫ f(x)dx =2 ∫ f(x)dx, Q=2 ∫ xdx Пусть теперь кривая, огран. площадь,
Пусть теперь кривая, огран. площадь, задана параметрически, т.е. в виде y = ψ(t), где α ≤ t ≤ β
задана параметрически, т.е. в виде y = ψ(t), где α ≤ t ≤ β