Сравнение и измерение углов.

Дидактический сценарий урока по теме

Свойство смежных и вертикальных углов»

Дата:__.___.2013

Учитель:Буяльская Алеся, студентка 404 группы математического факультета

Класс:7

Место урока в теме: второй урок из 4 по теме

Тип урока:комбинированный (закрепление знаний и умений, изучение нового материала).

Цели и задачи:

1.Образовательные:

• проверить знание определений понятий угла, развёрнутого угла, биссектрисы угла, градусной меры угла;
• обеспечить действенность этих знаний в знакомой и изменённой ситуации;
• сформировать понятия смежных и вертикальных углов;
• сформулировать теоремы о смежных и вертикальных углах, сформировать представление об основной цели их изучения в 7 классе: доказательство этих теорем;
• сформировать представления о плане изучения (воспроизведения) теоремы, об оформлении доказательства;
• доказать теоремы о смежных и вертикальных углах;
• продолжить формирование навыка их применения.

2.Развивающие:

• развивать логическое мышление учащихся путём формирования умения анализировать утверждения, делать обоснованные выводы на основе нескольких суждений; развивать пространственные представления учащихся в ходе построения графических моделей геометрических конструкций.

3.Воспитательные:

• воспитывать ответственное отношение к учебной деятельности, стимулировать познавательный интерес.

Структура урока:

1. Ориентировочно-мотивационный этап (2 мин).

1.1.приветствие;

1.2.сообщение направления деятельности;

1.3.постановка целей и задач урока.

2. Исполнительный этап

2.1 Закрепление знаний и умений

2.1.1. проверка знания материала предыдущего занятия и домашнего задания (5мин);

2.1.2. применение знаний в знакомой и изменённой ситуации (5мин).

2.2 Изучение нового материала

2.2.1 формулировка определений понятий смежных и вертикальных углов (5 мин);

2.2.2 мотивация деятельности по доказательству теорем о смежных и вертикальных углах(1мин);

2.2.3 доказательство теоремы о смежных углах и применение в знакомой ситуации (10 мин);

2.2.4 доказательство теоремы о вертикальных углах и применение в знакомой ситуации ( 10 мин);

3. Контрольно-оценочный этап (5мин);

4. Рефлексия. Постановка домашнего задания (2мин).

Средства обучения: Учебное пособие для 7 класса «Геометрия» Шлыков В.В.;

Презентация к уроку; карточки

Ход урока

№ этапа	Название этапа	Цель	Действия учителя	Действия учащихся
	Ориентировочно-мотивационный	Сориентировать учащихся в том, какие виды учебной деятельности они будут выполнять на уроке, мотивировать их учебную деятельность.	Учитель приветствует учащихся. Требует записать дату, «Классная работа». Напоминает тему, сообщает о том, что урок будет состоять из двух частей, подводит к осознанию отличий между изучением аналогичной темы в 5 классе и в 7 классе, формулирует цели урока.	Учащиеся приветствуют учителя, записывают дату, «Классная работа» осознают новый уровень изучения данной темы по отношению к уровню её изучения в 5 классе, осмысливают цели урока.

У: Здравствуйте, садитесь. Сегодня мы продолжим изучение темы прошлого урока и изучим новый материал. Какую тему мы изучали на прошлом уроке?

О: «Сравнение и измерение углов».

У: Какие понятия рассмотрели?

О: Угол, развёрнутый угол, биссектриса угла, градусная мера угла, прямой, острый, тупой угол.

У: Что же в этом нового? Ведь все эти понятия мы изучали в 5 классе?

О: Теперь мы изучаем эти понятия в системе: даём им строгие определения с использованием тех понятий, которые определены ранее.

У: Сегодня мы проверим, как вы усвоили новые определения известных вам понятий, а затем вспомним два знакомых вам геометрических факта о смежных и вертикальных углах, которые вы установили в 5 классе путём измерения, и строго докажем их. Запишите тему урока «Сравнение и измерение углов. Свойство смежных и вертикальных углов»

№ этапа	Название этапа	Цель	Действия учителя	Действия учащихся
2.1.1	Проверка знания материала предыдущего занятия и домашнего задания	Проверить знание определений понятий, изученных на прошлом уроке, и решения задач домашней работы	Учитель организует проверку знаний в форме игры «Очередь», опрашивая 5 человек. Если «очередь» быстро заканчивается, учитель вызывает следующих 5 учащихся. Предлагает двум учащимся подготовить на доске решения домашних задач.	5 учащихся по очереди отвечают на вопросы учителя, выбывая из очереди в случае неудовлетворительного ответа. Остальные в роли судей следят за правильностью ответов. Для каждого ответа судья выбирается случайным образом из числа остальных учащихся класса. Во время игры двое учащихся подготавливают решения домашних задач.

У: Проверку ваших теоретических знаний мы проведём в форме игры «Очередь»: пять человек по очереди отвечают на мои вопросы. Тот, кто ответил не верно – выбывает из очереди. Выигрывает тот, кто последним правильно ответил на вопрос. Этот ученик получает дополнительный балл к отметке за работу на уроке. Остальные учащиеся оценивают правильность ответов.

Пока мы будем играть в «Очередь» двое учащихся запишут на доске решения домашних задач и подготовятся кратко изложить их решение. Они так же получат дополнительный балл за работу на уроке.

№	Вопрос	Ответ
1.	На сколько частей разделяют плоскость два луча с общим началом?	На две
2.	Что пропущено в определении понятия луч: «Луч состоит из точки прямой и всех её точек, лежащих по одну сторону от данной точки»?	Родовое понятие «геометрическая фигура» «Луч – это геометрическая фигура, которая состоит из точки прямой и всех её точек, лежащих по одну сторону от данной точки
3.	Верно ли, что угол – это геометрическая фигура, которая состоит из двух лучей, имеющих общее начало?	В той теории, которую строим мы, это не верно
4.	Какую геометрическую фигуру мы называем углом?	Углом мы называем геометрическую фигуру, состоящую из двух лучей с общим началом и одной из частей плоскости, на которые эти лучи разделяют остальные точки плоскости.
5.	Какой угол называется развёрнутым?	Развернутым называется угол, стороны которого являются противоположными лучами.
6.	Какие лучи называются противоположными?	Два различных луча одной прямой, имеющие общее начало.
7.	Какие углы называются равными?	Те, которые можно совместить наложением
8.	Что такое биссектриса угла?	Биссектрисой угла называется луч с началом в вершине этого угла и делящий его на два равных угла.
9.	Что приняли за единицу измерения угла?	Угол в один градус.
10.	Что такое угол в один градус?	Угол, равный 1/180 части развернутого угла.
11.	Что такое градусная мера угла?	Геометрическая величина, которая показывает, сколько раз угол в один градус и его части укладываются в данном угле.
12.	Какова градусная мера развёрнутого угла?	180°
13.	Какой угол называется прямым?	Угол, градусная мера которого равна 90°.
14.	Какой угол называется тупым?	Угол, градусная мера которого больше 90° и меньше 180°.
15.	Какой угол называется острым?	Угол, градусная мера которого больше 0° и меньше 90°.
16.	Как вычислить градусную меру угла, разделённого лучом на две части?	Сложить градусные меры углов, на которые он делится этим лучом

У: Рассмотрим решения домашних задач

О:№79 стр. 72

Луч OS делит 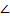AOB на два угла, один из которых в два раза больше другого. Вычислите градусную меру каждого из углов, если 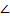AOB = 78°.

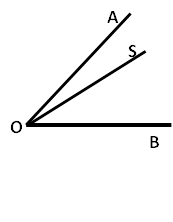Дано:

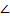AOB= 78°,

OS-луч,

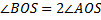
Найти:

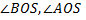
Решение

1)

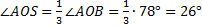
2)

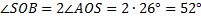
Ответ: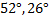

Стр. 73

Луч OK делит 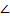BOC, градусная мера которого равна 160°, на два угла. Вычислите градусные меры угловВОК и КОС, если их разность равна 24° и угол ВОК больше угла КОС.

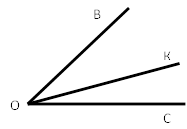Дано

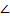BOC=160°,

ОК-луч

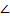ВОК - 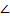КОС=24°

Найти

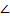ВОК и 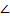КОС

Решение

1)

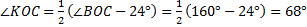
2)

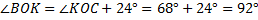
Ответ: 92°, 68°.

№ этапа	Название этапа	Цель	Действия учителя	Действия учащихся
2.1.2	Применение знаний в знакомой и изменённой ситуации	Организовать деятельность учащихся, направленную на закрепление умения применять определения изученных понятий и свойства градусной меры углов в знакомой и изменённой ситуации	Учитель организует устную работу учащихся по применению знаний в знакомой ситуации, используя задачи на готовых чертежах. Для работы по закреплению умения применять знания в изменённой ситуации организует самостоятельную работу учащихся, а двух учеников вызывает для решения этих задач на обратной стороне доски.	Отвечают на вопросы учителя, решают устные задачи по готовому чертежу. После этого двое учащихся решают задачу №91 на обратной стороне доски, все остальные самостоятельно решают задачу в тетрадях, затем сверяют решения.

У: (слайд 1) Устно ответьте на вопросы:

1. 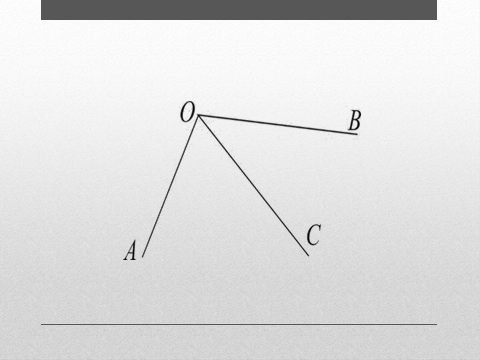Сколько углов изображено на чертеже? (6)

2. Какие углы нужно рассматривать при решении задач, если нет дополнительных замечаний? (Не превосходящие развёрнутого)

3. Вычислите градусную меру угла AOC, если градусная мера угла AOB равна 110°, а градусная мера угла BOC на 40° меньше градусной меры угла AOC . (75°)

4. Вычислите градусную меру угла BOC, если она вдвое меньше градусной меры угла AOC. Известно, что градусная мера угла AOB равна 120°. (40°)

У:Решите в тетрадях задачу №91 стр. 74,двое учащихся будут решать за доской, после мы сверим решения.

«Луч ОС делит угол АОВ на два угла так, что ÐAOC = 3ÐCOB. Луч OD проведен так, что луч OA является биссектрисой угла DOB. Вычислите градусные меры углов АОС, СОВ и DOB, если ÐAOB = 60°»

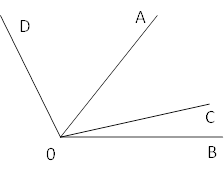Решение

1) 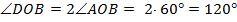, т.к. OA –биссектриса ÐDOB.

2) ÐCOB = =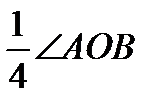

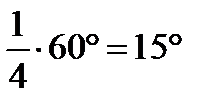
3) ÐAOC = 3ÐCOB = 3×15°=45°

Ответ: 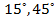,120˚

У: Как иначе можно было решить задачу? Какие утверждения геометрической теории использовались при решении?

№ этапа	Название этапа	Цель	Действия учителя	Действия учащихся
2.2.1	Формулировка определений понятий смежных и вертикальных углов	Организовать деятельность учащихся по формулировке и запоминанию определений понятий смежных и вертикальных углов	Учитель задает учащимся вопросы для того, чтобы подвести к определениям понятий смежных и вертикальных углов, приводит контрпримеры, позволяющие выявить существенные свойства этих понятий	Отвечают на вопросы учителя, выявляют существенные свойства понятий смежных и вертикальных углов, формулируют и запоминают определения

А

С

О

В

У: Рассмотрим развернутый угол - ÐAOC, разобьём его лучом OB на два угла – угол ÐAOB иÐBOC. Как называется пара углов ÐAOB иÐBOC?

О: Смежные углы.

У: Правильно, понятие смежных углов нам уже знакомо из 5 класса. Теперь давайте дадим строгое определение с использованием тех понятий, которые определены ранее. Какое бы вы определение дали смежным углам?

О: Два угла имеющие общую сторону называются смежными.

А

С

D

F

У: Посмотрите на рисунок, пара углов ÐADF и ÐFDC имеют общую сторону FD, но будут ли они смежными?

О: Нет.

У: Как тогда нам уточнить определение?

О: Два угла, у которых есть одна общая сторона, а две другие являются противоположенными лучами называются смежными.

А

С

О

В

D

У: Запишем полученное определениев тетрадь, и будем его в дальнейшем использовать. Сегодня на уроке мы воспользуемся им при доказательстве свойства смежных углов, но это будет чуть позже.

У: Рассмотрим две пересекающиеся прямые AC и BD.Нам уже известно, что прямые могут иметь только одну общую точку, если они различны и не параллельны. Назовем эту точку О. Как называют пару углов ÐAOB иÐDOC?

О: Вертикальные углы.

У: Верно, это понятие тоже вам знакомо. А теперь давайте дадим строгое определение этой паре углов. Какое бы вы определение дали вертикальным углам?

О: Два угла имеющие общую точку называются вертикальными.

А

С

D

F

P

У: Посмотрите на рисунок, пара углов ÐADF и ÐPDC имеет общую точку D, но будут ли они вертикальными?

О: Нет.

У: Что еще нам нужно учесть при составлении определения?

О: Что стороны одного углаявляются лучами, противоположными сторонам другого.

У: Верно, теперь объедините все сказанное и дайте определение вертикальных углов.

О: Два угла, у которых есть общая точка, и стороны одного угла являются лучами, противоположными сторонам другого, называются вертикальными.

У: Верно, запишите полученное определение в тетрадь.

А

С

D

F

P

V

У: Посмотрите на рисунок, будет ли пара ÐADF и ÐPVC вертикальными углами?

О: Нет.

У: Почему, ведь у них есть общая точка D, а AD и DC– это противоположенные лучи?

О: Чтобы ÐADF и ÐPVC были вертикальными по определению, FD и VP то же должны быть противоположенными лучами, а это не так.

№ этапа	Название этапа	Цель	Действия учителя	Действия учащихся
2.2.2	Мотивация деятельности по доказательству теорем о смежных и вертикальных углах	Мотивировать деятельность учащихся по доказательству известных ранее теорем, сориентировать в том, какова основная цель второй части урока.	Подводит к осознанию необходимости доказательства всех изученных ранее и новых геометрических фактов, формулирует цель второй части урока	Учащиеся осознают необходимость доказательства геометрических фактов, осмысливают цели второй части урока.

У: Ребята, какие вы знаете свойства смежных и вертикальных углов из 5 класса?

О: Сумма смежных углов равна 180°, вертикальные углы равны.

У: А как вы узнали об этих свойствах?

О: Прочитали в книжке, измерили углы нескольких пар смежных углов.

У: Как вы думаете, сколько нужно сделать измерений, чтобы убедиться, что этими свойствами обладают все смежные (вертикальные) углы?

О: Сколько бы мы не сделали измерений, мы не получим точного доказательства.

У: Сегодня мы докажем эти утверждения точно, на основании изученных ранее определений, аксиом и теорем.

№ этапа	Название этапа	Цель	Действия учителя	Действия учащихся
2.2.3	Доказательство теоремы о смежных углах и применение в знакомой ситуации	Организовать деятельность учащихся по формулировке и доказательству теоремы о смежных углах, и применению её в знакомой ситуации	Учитель задает учащимся наводящие вопросы для того, чтобы подвести их к доказательству теоремы о смежных углах, предлагает задачи	Отвечают на вопросы учителя, формулируют и доказывают теорему, опираясь на ранее изученные определения и теоремы, решают задачи

У: Докажем теорему о сумме градусных мер смежных углов. Вначале чтобы понять, что дано, а что нужно доказать, переформулируем теорему в форме «Если…, то…». Как тогда будет звучать формулировка теоремы?

О: Если даны два смежных угла, то сумма их градусных мер равна 180°.

У: Итак, что дано и что нужно доказать?

О: Даны два смежных угла, а доказать нужно что сумма их градусных мер равна 180°.

У: Хорошо, теперь давайте сделаем рисунок и запишем для него что дано и что нужно доказать.

А

С

О

В

Дано: ÐAOB и ÐBOC – смежные

Доказать: ÐAOB+ ÐBOC = 180°

У: Проанализируем условие. Что дано?

О: ÐAOB и ÐBOC – смежные.

У: Что это означает?

О: По определению смежными называются углы, у которых одна сторона общая, а две другие являются противоположными лучами.

У: Какой вывод можно сделать по имеющимся данным?

О: Что углы ÐAOB и ÐBOC вместе составляют развёрнутый угол AOC.

У: Каким свойством обладает развёрнутый угол?

О: Его градусная мера равна 180°.

У: Какой можно сделать вывод?

О: Сумма градусных мер углов ÐAOB и ÐBOC равна 180°

У: Это и требовалось доказать. Вернёмся к началу: что было дано, что требовалось доказать? Как мы это сделали? Какие утверждения геометрической теории использовали?

Запишем в тетрадь доказательство:

1) ÐAOB и ÐBOC - смежные, значит лучи OC и OA – противоположные (по определению смежных углов), значит, ÐAOC – развернутый (по определению развёрнутого угла).

2) ∠AOB + ∠BOC = 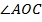(по свойству градусной меры углов)

ÐAOB+ ÐBOC = 180°

3) ÐAOC=180° (по свойству развёрнутого угла)

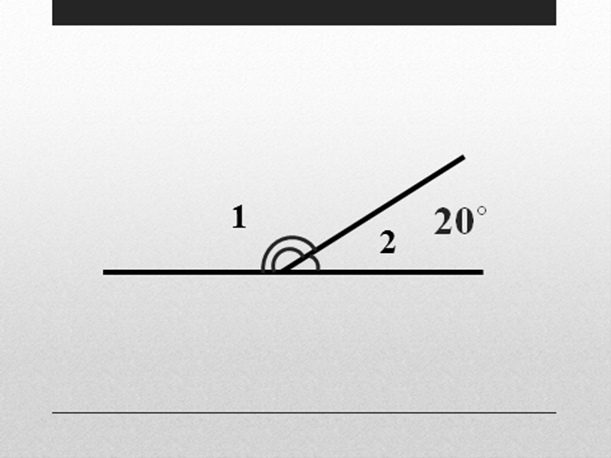У: (слайд 2) Посмотрите на рисунок, как называются углы 1 и 2?

О: Смежные.

У: Найдите градусную меру угла 1.

О: 160˚

У: На основании чего вы сделали такой вывод?

О: На основании теоремы о смежных углах. Согласно этой теореме сумма градусных мер углов 1 и 2 равна 180°. По условию градусная мера угла 2 равна 20°, значит, градусная мера угла 1 равна 180°-20°=160°.

У: Решение задачи №95 на стр.75.запишем в тетрадь.

Идея решения задачи обсуждается, затем образец решения записывается одним из учеников на доске.

На стр.75

«Градусная мера одного из смежных углов в три раза меньше градусной меры другого угла. Вычислите градусную меру каждого из углов»

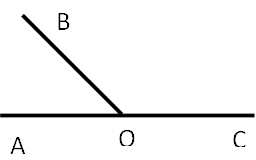
Дано:ÐAOB и ÐBOC – смежные

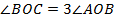
Найти:

Решение

1) 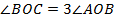(по условию) ÐAOB= ,

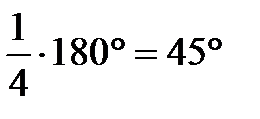2) ÐAOB+ ÐBOC = 180° (по свойству смежных углов )

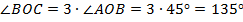
Ответ: ,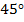

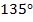
№ этапа	Название этапа	Цель	Действия учителя	Действия учащихся
2.2.4	Доказательство теоремы о вертикальных углах и её применение в знакомой ситуации	Организовать деятельность учащихся по формулировке и доказательству теоремы о вертикальных углах, и применению её в знакомой ситуации	Учитель задает учащимся наводящие вопросы для того, чтобы подвести их к доказательству теоремы о вертикальных углах, предлагает задачи.	Отвечают на вопросы учителя, формулируют и доказывают теорему, опираясь на ранее изученные определения и теоремы, решают задачи

У: Сейчас мы докажем утверждение о том, что вертикальные углы равны. А как называется утверждение, требующее доказательства?

О: Теорема.

У: Переформулируйте теорему о свойстве вертикальных углов в форме «Если…, то…»

О: Если даны два вертикальных угла, то они равны между собой.

У: Что дано, что требуется доказать?

О: Даны два вертикальных угла, нужно доказать что они равны.

У: Сделаемрисунок, иллюстрирующий теорему, и запишем для него что дано и что нужно доказать.

Дано: ÐAOB и ÐDOC

А

С

О

В

D

– вертикальные углы

Доказать: ÐAOB= ÐDOC

У: Какой вывод можно сделать по имеющимся данным?

О: Согласно определению вертикальных углов лучи ОВ и OD – противоположные, они составляют прямую BD, лучи ОA и OС – противоположные, они составляют прямую AC.

У: Какие пары углов образуются при пересечении двух прямых?

О: Пары смежных и вертикальных углов.

У: Что требуется доказать?

О: Что ÐAOB= ÐDOC.

У: Как это сделать, опираясь на свойство смежных углов?

О: Найти угол, который является смежным для углов ÐAOB и ÐDOC.

У: Найдите такой угол.

О: Например, ∠AOD

У: Запишем свойство смежных углов для каждой пары?

О: ∠AOB + ∠AOD =180˚

∠DOC + ∠AOD=180˚

У: Выразите из полученных равенств ∠AOB и ∠DOC.

О: ∠AOB = 180˚– ∠AOD

∠DOC = 180˚– ∠AOD

У: Какой вывод можно сделать?

О: Градусные меры углов ÐAOB иÐDOC равны, а значит ÐAOB= ÐDOC

У: Теорема доказана. Вернёмся к началу: что было дано, что требовалось доказать? Как мы это сделали?

Запишем в тетрадь доказательство:

∠AOB + ∠AOD =180˚ (по св. смежных углов), отсюда ∠AOB = 180˚– ∠AOD

ÐAOB= ÐDOC

∠DOC + ∠AOD=180˚ (по св. смежных углов), отсюда ∠DOC = 180˚– ∠AOD

У: Перейдем к применению этой теоремы. 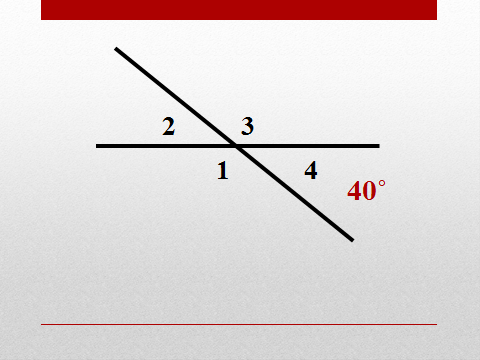(Слайд 3) Посмотрите на рисунок, какие углы изображены на слайде?

О: Смежные и вертикальные.

У: Сколько пар вертикальных углов? Назовите их.

О: Две пары: 2 и 4 , 1 и 3

У: Сколько пар смежных углов? Назовите их.

О: Четыре пары: 1и 2, 2 и 3, 3 и 4, 4 и 1.

У: Найдите градусную меру углов 1, 2 и 3; ответ обоснуйте.

О: Углы 2 и 4 – вертикальные, а значит по теореме о свойстве вертикальных углов, они равны. Известно, что градусная мера угла 4 равна 40°, значит Ð2=40˚.

Углы 1 и 4 – смежные, а значит по теореме о свойстве смежных углов сумма их градусных мер равна 180°. Известно, что градусная мера угла 4 равна 40°, а значит Ð1=180˚ - 40°=140°.

Углы 1 и 3 – вертикальные, а значит по теореме о вертикальных углах они равны. Известно, что градусная мера угла 1 равна 140°, а значит Ð3=140˚.

№ этапа	Название этапа	Цель	Действия учителя	Действия учащихся
	Контрольно-оценочный этап	Выявить уровень усвоения определений понятий и теорем, изученных на уроке	Учитель организует проверку знаний в форме игры. Каждому ученику, сидящему на последней парте, раздается карточка с задачами, он должен решить первую задачу, записать полученный ответ и передать карточку ученику, сидящему впереди него. Тот должен решить следующую задачу и передать карточку дальше по цепочке. Выигрывает та команда, которая быстрее всех решит правильно все задачи.	Учащиеся участвуют в игре, решая свою задачу и передавая карточку по цепочке дальше.

У: Ребята, сейчас мы сыграем в игру, чтобы проверить, как вы усвоили новую тему. Мы разделимся на шесть команд. Посмотрите на тех, кто сидит перед вами и позади, ваш ряд – это ваша команда. У каждой команды будет карточка с заданиями, всего 5 задач на каждого члена команды по одной. Я раздам карточки ребятам, сидящим на последней парте, по сигналу начала нашей игры они должны будут перевернуть карточки, решить первую задачу, записать ответ и передать карточку впереди сидящему игроку своей команды. Тот в свою очередь решает следующую задачу, записывает ответ и передаёт карточку дальше по цепочке. Когда к вам попадет карточка, вверху своей задачи вы найдете выражение, которое пояснит, как получить дано для своей задачи из ответа предыдущей. Поэтому, если хотя бы одну задачу решить неверно, то и все последующие задачи будут решены неверно, будьте внимательны. На обратной стороне доски записаны ответы для последней задачи, команда, которая быстрее всех получит правильный ответ, заработает оценки за работу на уроке.

	Вариант 1	Вариант 2
№1	A O L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAllbEw8UA AADbAAAADwAAAGRycy9kb3ducmV2LnhtbESPS4vCQBCE7wv7H4Ze8LZODPgg6ygSkBXRg4+Lt95M mwQzPdnMqNFf7wiCx6KqvqLG09ZU4kKNKy0r6HUjEMSZ1SXnCva7+fcIhPPIGivLpOBGDqaTz48x JtpeeUOXrc9FgLBLUEHhfZ1I6bKCDLqurYmDd7SNQR9kk0vd4DXATSXjKBpIgyWHhQJrSgvKTtuz UbBM52vc/MVmdK/S39VxVv/vD32lOl/t7AeEp9a/w6/2QisYxvD8En6AnDwAAAD//wMAUEsBAi0A FAAGAAgAAAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54 bWxQSwECLQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJl bHNQSwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBl eG1sLnhtbFBLAQItABQABgAIAAAAIQCWVsTDxQAAANsAAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMv ZG93bnJldi54bWxQSwUGAAAAAAQABAD1AAAAigMAAAAA " filled="f" stroked="f" strokeweight=".5pt"> C B L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAdvP5LMUA AADbAAAADwAAAGRycy9kb3ducmV2LnhtbESPT4vCMBTE7wt+h/AEb2uqrKtUo0hBVsQ9+Ofi7dk8 22LzUpuo1U+/WRA8DjPzG2Yya0wpblS7wrKCXjcCQZxaXXCmYL9bfI5AOI+ssbRMCh7kYDZtfUww 1vbOG7ptfSYChF2MCnLvq1hKl+Zk0HVtRRy8k60N+iDrTOoa7wFuStmPom9psOCwkGNFSU7peXs1 ClbJ4hc3x74ZPcvkZ32aV5f9YaBUp93MxyA8Nf4dfrWXWsHwC/6/hB8gp38AAAD//wMAUEsBAi0A FAAGAAgAAAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54 bWxQSwECLQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJl bHNQSwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBl eG1sLnhtbFBLAQItABQABgAIAAAAIQB28/ksxQAAANsAAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMv ZG93bnJldi54bWxQSwUGAAAAAAQABAD1AAAAigMAAAAA " filled="f" stroked="f" strokeweight=".5pt"> 36° Найти: ÐAOB=	A O L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAPB2PCMMA AADbAAAADwAAAGRycy9kb3ducmV2LnhtbERPy2qDQBTdF/IPww1014wRWsRkFBGkpbSLPDbZ3Tg3 KnHuGGdqbL++syh0eTjvbT6bXkw0us6ygvUqAkFcW91xo+B4qJ4SEM4ja+wtk4JvcpBni4ctptre eUfT3jcihLBLUUHr/ZBK6eqWDLqVHYgDd7GjQR/g2Eg94j2Em17GUfQiDXYcGlocqGypvu6/jIL3 svrE3Tk2yU9fvn5ciuF2PD0r9biciw0IT7P/F/+537SCJKwPX8IPkNkvAAAA//8DAFBLAQItABQA BgAIAAAAIQDw94q7/QAAAOIBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1s UEsBAi0AFAAGAAgAAAAhADHdX2HSAAAAjwEAAAsAAAAAAAAAAAAAAAAALgEAAF9yZWxzLy5yZWxz UEsBAi0AFAAGAAgAAAAhADMvBZ5BAAAAOQAAABAAAAAAAAAAAAAAAAAAKQIAAGRycy9zaGFwZXht bC54bWxQSwECLQAUAAYACAAAACEAPB2PCMMAAADbAAAADwAAAAAAAAAAAAAAAACYAgAAZHJzL2Rv d25yZXYueG1sUEsFBgAAAAAEAAQA9QAAAIgDAAAAAA== " filled="f" stroked="f" strokeweight=".5pt"> C B L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAo4O05MQA AADbAAAADwAAAGRycy9kb3ducmV2LnhtbESPT4vCMBTE78J+h/AWvGm6BaV0jSIFURY9+Oeyt2fz bIvNS7fJavXTG0HwOMzMb5jJrDO1uFDrKssKvoYRCOLc6ooLBYf9YpCAcB5ZY22ZFNzIwWz60Ztg qu2Vt3TZ+UIECLsUFZTeN6mULi/JoBvahjh4J9sa9EG2hdQtXgPc1DKOorE0WHFYKLGhrKT8vPs3 Cn6yxQa3x9gk9zpbrk/z5u/wO1Kq/9nNv0F46vw7/GqvtIIkhueX8APk9AEAAP//AwBQSwECLQAU AAYACAAAACEA8PeKu/0AAADiAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnht bFBLAQItABQABgAIAAAAIQAx3V9h0gAAAI8BAAALAAAAAAAAAAAAAAAAAC4BAABfcmVscy8ucmVs c1BLAQItABQABgAIAAAAIQAzLwWeQQAAADkAAAAQAAAAAAAAAAAAAAAAACkCAABkcnMvc2hhcGV4 bWwueG1sUEsBAi0AFAAGAAgAAAAhAKODtOTEAAAA2wAAAA8AAAAAAAAAAAAAAAAAmAIAAGRycy9k b3ducmV2LnhtbFBLBQYAAAAABAAEAPUAAACJAwAAAAA= " filled="f" stroked="f" strokeweight=".5pt"> 44° Найти: ÐAOB =
№2	ÐAOB =2ÐFEK   L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAQyaJC8YA AADbAAAADwAAAGRycy9kb3ducmV2LnhtbESPQWvCQBSE7wX/w/KE3upGaSWkrhICwVLag9GLt9fs Mwlm38bs1qT99d2C4HGYmW+Y1WY0rbhS7xrLCuazCARxaXXDlYLDPn+KQTiPrLG1TAp+yMFmPXlY YaLtwDu6Fr4SAcIuQQW1910ipStrMuhmtiMO3sn2Bn2QfSV1j0OAm1YuomgpDTYcFmrsKKupPBff RsF7ln/i7mth4t82236c0u5yOL4o9Tgd01cQnkZ/D9/ab1pB/Az/X8IPkOs/AAAA//8DAFBLAQIt ABQABgAIAAAAIQDw94q7/QAAAOIBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10u eG1sUEsBAi0AFAAGAAgAAAAhADHdX2HSAAAAjwEAAAsAAAAAAAAAAAAAAAAALgEAAF9yZWxzLy5y ZWxzUEsBAi0AFAAGAAgAAAAhADMvBZ5BAAAAOQAAABAAAAAAAAAAAAAAAAAAKQIAAGRycy9zaGFw ZXhtbC54bWxQSwECLQAUAAYACAAAACEAQyaJC8YAAADbAAAADwAAAAAAAAAAAAAAAACYAgAAZHJz L2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA9QAAAIsDAAAAAA== " filled="f" stroked="f" strokeweight=".5pt"> G D E F K Найти: ÐGED =	ÐAOC =2ÐFEK   L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAxv8f1sYA AADbAAAADwAAAGRycy9kb3ducmV2LnhtbESPQWvCQBSE74L/YXmF3nTTYMWmriKBYCl6SOqlt9fs MwnNvo3Zrab+elco9DjMzDfMcj2YVpypd41lBU/TCARxaXXDlYLDRzZZgHAeWWNrmRT8koP1ajxa YqLthXM6F74SAcIuQQW1910ipStrMuimtiMO3tH2Bn2QfSV1j5cAN62Mo2guDTYcFmrsKK2p/C5+ jIL3NNtj/hWbxbVNt7vjpjsdPp+VenwYNq8gPA3+P/zXftMKXmZw/xJ+gFzdAAAA//8DAFBLAQIt ABQABgAIAAAAIQDw94q7/QAAAOIBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10u eG1sUEsBAi0AFAAGAAgAAAAhADHdX2HSAAAAjwEAAAsAAAAAAAAAAAAAAAAALgEAAF9yZWxzLy5y ZWxzUEsBAi0AFAAGAAgAAAAhADMvBZ5BAAAAOQAAABAAAAAAAAAAAAAAAAAAKQIAAGRycy9zaGFw ZXhtbC54bWxQSwECLQAUAAYACAAAACEAxv8f1sYAAADbAAAADwAAAAAAAAAAAAAAAACYAgAAZHJz L2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA9QAAAIsDAAAAAA== " filled="f" stroked="f" strokeweight=".5pt"> G D E F K Найти: ÐGED =
№3	ÐGED =ÐBOC E F B A O D C Найти: ÐCOD=	ÐGED =ÐBOC E F B A O D C Найти: ÐCOD=
№4	ÐCOD=ÐLOB A O B L 90° L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAcBcrt8MA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbERPS4vCMBC+L/gfwgje1lRZV6lGkYKsiHvwcfE2NmNb bCa1iVr99ZsFwdt8fM+ZzBpTihvVrrCsoNeNQBCnVhecKdjvFp8jEM4jaywtk4IHOZhNWx8TjLW9 84ZuW5+JEMIuRgW591UspUtzMui6tiIO3MnWBn2AdSZ1jfcQbkrZj6JvabDg0JBjRUlO6Xl7NQpW yeIXN8e+GT3L5Gd9mleX/WGgVKfdzMcgPDX+LX65lzrM/xrC/zPhAjn9AwAA//8DAFBLAQItABQA BgAIAAAAIQDw94q7/QAAAOIBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1s UEsBAi0AFAAGAAgAAAAhADHdX2HSAAAAjwEAAAsAAAAAAAAAAAAAAAAALgEAAF9yZWxzLy5yZWxz UEsBAi0AFAAGAAgAAAAhADMvBZ5BAAAAOQAAABAAAAAAAAAAAAAAAAAAKQIAAGRycy9zaGFwZXht bC54bWxQSwECLQAUAAYACAAAACEAcBcrt8MAAADcAAAADwAAAAAAAAAAAAAAAACYAgAAZHJzL2Rv d25yZXYueG1sUEsFBgAAAAAEAAQA9QAAAIgDAAAAAA== " filled="f" stroked="f" strokeweight=".5pt"> K Найти: ÐKOA=	ÐCOD=ÐLOB A O B L 90° L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAhFEpGMcA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbESPT2vCQBDF7wW/wzJCb3WjYJHUjUhALKU9qLl4m2Yn fzA7G7NbTfvpO4dCbzO8N+/9Zr0ZXaduNITWs4H5LAFFXHrbcm2gOO2eVqBCRLbYeSYD3xRgk00e 1phaf+cD3Y6xVhLCIUUDTYx9qnUoG3IYZr4nFq3yg8Mo61BrO+Bdwl2nF0nyrB22LA0N9pQ3VF6O X87AW777wMPnwq1+unz/Xm37a3FeGvM4HbcvoCKN8d/8d/1qBX8ptPKMTKCzXwAAAP//AwBQSwEC LQAUAAYACAAAACEA8PeKu/0AAADiAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNd LnhtbFBLAQItABQABgAIAAAAIQAx3V9h0gAAAI8BAAALAAAAAAAAAAAAAAAAAC4BAABfcmVscy8u cmVsc1BLAQItABQABgAIAAAAIQAzLwWeQQAAADkAAAAQAAAAAAAAAAAAAAAAACkCAABkcnMvc2hh cGV4bWwueG1sUEsBAi0AFAAGAAgAAAAhAIRRKRjHAAAA3AAAAA8AAAAAAAAAAAAAAAAAmAIAAGRy cy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPUAAACMAwAAAAA= " filled="f" stroked="f" strokeweight=".5pt"> K Найти: ÐKOA=
№5	ÐKOA=ÐPLZ G P L F Z Найти: ÐPLG	ÐKOA=ÐPLZ G P L F Z Найти: ÐPLG

Оценки за урок получают_____________________________

№ этапа	Название этапа	Цель	Действия учителя	Действия учащихся
	Рефлексия. Постановка домашнего задания	Подвести итоги работы на уроке	Учитель подводит итоги изученного на уроке; раздает каждому ученику карточку для оценивания его работы на уроке. Задает и поясняет ученикам домашнее задание.	Учащиеся заполняют карточки, оценивая свою работу на уроке. Записывают домашнее задание в дневники, слушают пояснения к задачам.

У: Что нового было на сегодняшнем уроке?

О: Сегодня на уроке мы дали строгое определение смежным и вертикальным углам. Доказали теоремы о смежных и вертикальных углах, а так же применили их при решении задач.

Учащимся раздаются карточки для оценивания своей работы на уроке

1.Своей работой на уроке я 2.Урок для меня показался 3.За урок я 4.Мое настроение 5.Материал урока мне был

доволен / не доволен коротким / длинным не устал / устал стало лучше / стало хуже понятен / не понятен

У: Ребята, откройте дневники и запишите домашнее задание на следующий урок. Стр74 №96,92

При решении №92, вам нужно будет вспомнить, как мы решали в классе №91 и №95, для решения задачи необходимо будет опираться на два этих номера. В №96 вам нужно будет воспользоваться свойствами, которые мы сегодня изучили.