Определение высоты водонапорной башни
Для определения высоты водонапорной башни сначала рассчитываем потери напора по длине на всех участках магистрального трубопровода по формуле:
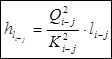 , (1.5)
, (1.5)
где Ki-j - коэффициент расхода , л/с.
Вычисляя потери напора по длине, в числитель этой формулы будем подставлять квадрат усреднённого значения коэффициента расхода для каждой трубы магистрали, значение которого будем брать из справочного материала (табл. 4.5, стр.39, [1] ) в зависимости от диаметра соответствующей трубы:
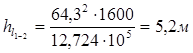 ,
,
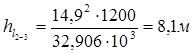 ,
,
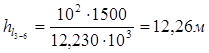 .
.
Высота башни рассчитывается по формуле:
HБ = Ñ /1 - Ñ1 , (1.6)
где HБ - высота башни, м; Ñ1 - отметка точки 1, м; Ñ /1 - пьезометрическая отметка точки 1, м, которая, в свою очередь, рассчитывается следующим образом:
Ñ /1 = Ñ6 + 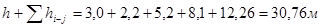
Тогда высота башни, согласно формуле (1.6), будет равна:
HБ = 30,76 – 4,9 = 25,86 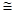 25,9 м
25,9 м
Расчет ответвлений
Расчет ответвления 3-4
Определим расход на участке 3-4:
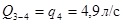
Расчетную потерю напора по длине находим как разницу пьезометрических отметок точек 3 и 4:
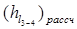 = Ñ /3 -Ñ /4 , (1.7)
= Ñ /3 -Ñ /4 , (1.7)
Пьезометрические отметки точек находим по формулам:
Ñ /4 = Ñ4 + h , (1.8)
где Ñ4 - отметка точки 4, м; h - наименьшее допустимое возвышение пьезометрической линии над поверхностью земли, м;
Ñ /3 =Ñ /6 + 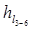 , (1.9)
, (1.9)
где пьезометрическая отметка точки 6 определяется какÑ /6 =Ñ4 + h, м;
Указанные выше величины равны:
Ñ /3 = 3,0 + 2,2 + 12,26 = 17,46м;
Ñ /4 = 3 + 2,2 = 5,2м;
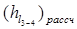 = 17,46 – 5,2 = 12,26м.
= 17,46 – 5,2 = 12,26м.
С другой стороны, потеря напора по длине может быть выражена по формуле (1.5), откуда получаем:
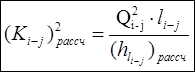 (1.10)
(1.10)
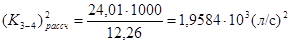
По соответствующим таблицам (табл. 4.5, стр.39, [1]) находим ближайшее большее стандартное значение коэффициента расхода 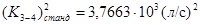 и соответствующее ему значение диаметра
и соответствующее ему значение диаметра 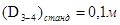 .
.
Так как диаметр трубы был взят стандартного значения, т.е. отличного от рассчитанного, действительное значение потери напора по длине будет отличаться от расчетного. Действительное значение потери напора вычислим по формуле (1.5), подставив туда сортаментное значение коэффициента расхода:
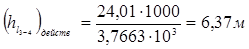 .
.
Расчет ответвления 2-5
Определим расчетный напор на участке 2-5 по формуле:
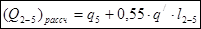 (1.11)
(1.11)
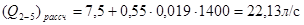
Расчетную потерю напора по длине находим по формуле:
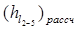 = Ñ /2 - Ñ /5 , (1.12)
= Ñ /2 - Ñ /5 , (1.12)
где пьезометрические высоты точек 2 и 5 соответственно равны:
Ñ /2 = Ñ /3 + 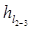 = 17,46 + 8,1 = 25,56 м;
= 17,46 + 8,1 = 25,56 м;
Ñ /5 = Ñ 5 + h = 3,5 + 2,2 = 5,7 м.
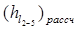 = 25,56 – 5,7 =19,86 м.
= 25,56 – 5,7 =19,86 м.
Квадрат расчетного коэффициента расхода находим по формуле (1.10):
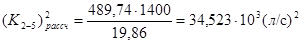
По соответствующим таблицам (табл. 4.5, стр.39, [1]) находим ближайшее большее стандартное значение коэффициента расхода 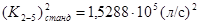 и соответствующее ему значение диаметра
и соответствующее ему значение диаметра 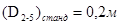 .
.
Определим действительное значение потери напора:
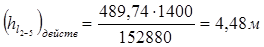 .
.
Расчет водопровода
Определение расходов 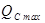 ,
, 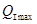 и
и 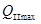
Определять расходы 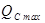 ,
, 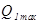 и
и 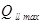 будем при условии полного открытия крана в точке С.
будем при условии полного открытия крана в точке С.
Составим уравнения из выражений для потерь напора по длине на всех участках:
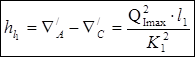 (2.1)
(2.1)
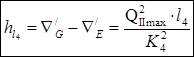 (2.2)
(2.2)
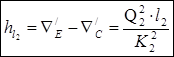 (2.3)
(2.3)
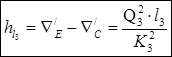 (2.4)
(2.4)
Вычислим значение 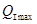 из формулы (2.1):
из формулы (2.1):
Ñ /A = zВ + hБ1 = 3,8 + 10,4 = 14,2 м;
Ñ /C = zC = 2,2 м;
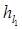 = 14,2 – 2,2 = 12 м;
= 14,2 – 2,2 = 12 м;
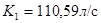 для диаметра трубы
для диаметра трубы 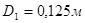 (табл. 4.5, стр.39, [1]);
(табл. 4.5, стр.39, [1]);
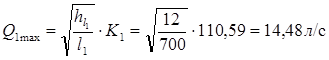 .
.
Для нахождения расхода 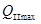 рассмотрим движение жидкости сразу на двух участках - на 4-ом и на участке, где трубопровод разветвляется:
рассмотрим движение жидкости сразу на двух участках - на 4-ом и на участке, где трубопровод разветвляется:
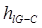 =Ñ /G - Ñ /C = h4 + h2 =
=Ñ /G - Ñ /C = h4 + h2 = 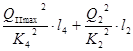 (2.5)
(2.5)
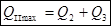 (2.6)
(2.6)
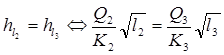 (2.7)
(2.7)
Подставляя известные величины в уравнение (2.7), получаем соотношение между расходами в параллельных ветвях трубопровода:
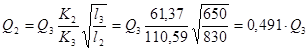 , (2.8)
, (2.8)
где значения K2 = 61,37л/с для D2 = 0,1м и K3 = 110,59л/с для D3 = 0,125м (из табл. 4.5, стр.39, [1]).
Подставляем соотношение (2.8) в (2.6), получаем:
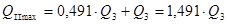 (2.9)
(2.9)
Вычисляем потерю по длине на этом участке:
hG -C = Ñ /G - Ñ /C 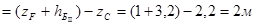
Подставляем полученные соотношения (2.8), (2.9) и известные величины в уравнение (2.5):
2 = 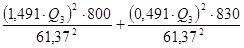
(K4 = 61,37л/с для D4 = 0,1м по табл. 4.5, стр.39, [1]);
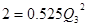
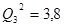
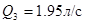
По формуле (2.9) получаем:
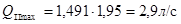 .
.
Расход из крана в точке С ищется по формуле:
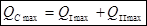 (2.10)
(2.10)
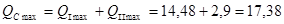 л/с.
л/с.
Определим значение 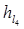 по формуле (2.2):
по формуле (2.2):
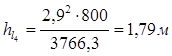 .
.
Построение кривой зависимости 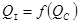 и
и 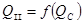
Полагаем, что открытие крана в точке С изменяется от 0 до 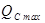 . Для построения графика рассмотрим частные случаи:
. Для построения графика рассмотрим частные случаи:
а) 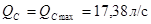 ;
; 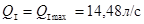 ;
; 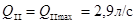 .
.
б) 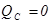 ;
; 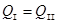 .
.
Рассмотрим движение жидкости по всему трубопроводу, разность отметок уровней воды в баке I и баке II будет являться суммой всех потерь напора по длине:
Ñ /A - Ñ /G 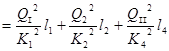 (2.11)
(2.11)
Учитывая равенство 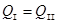 и выражения (2.8) и (2.9), получаем:
и выражения (2.8) и (2.9), получаем:
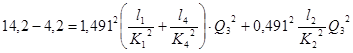 .
.
Подставляем известные величины:
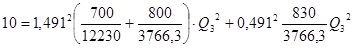
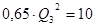
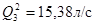
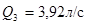
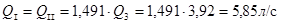
б) Бак II не работает: 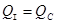 ,
, 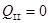 .
.
Ñ /A - Ñ /G 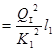 (2.12)
(2.12)
Подставляем известные значения:
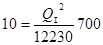
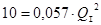
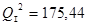
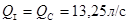 .
.
По найденным выше данным строим график зависимости 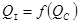 и
и 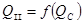 .
.
