Вывод закона Ома на основе электронной теории электропроводности металлов.

В электронной теории проводимости предполагается:

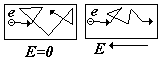1) В металлах имеются свободные электроны, которые в отсутствие внешнего

электрического поля движутся хаотически, а при

наличии поля приобретают характер упорядоченного

движения (см.рис.).

2) Движение каждого электрона подчиняется законам

классической механики.

3) Все вместе электроны образуют электронный газ и подчиняются законам

молекулярной физики.

4) Взаимодействие электронов с ионами решетки рассматривается как простое

столкновение, взаимодействием электронов между собой пренебрегается.

5) Напряженность поля внутри металла считается постоянной.

6) Все электроны под действием внешнего электрического поля приобретают

одинаковые скорости v_ср.

При выводе закона Ома будем считать, что электрон, сталкиваясь с ионом, полностью отдает ему свою энергию, а затем снова набирает скорость под действием сил поля (см. рис.- фрагмент кристаллической решетки). Электрон в кристалле участвует одновременно в двух движениях: хаотическом тепловом со скоростью u @ 10⁵ м/с и направленном под действием поля со скоростью v_ср порядка 0,001 м/с, т.е. u >> v_ср

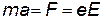	II закон Ньютона для электрона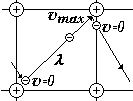
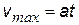	из кинематики, t – время движения электрона между двумя столкновениями
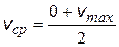	средняя скорость электрона за время между двумя столкновениями
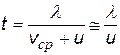	l - средняя длина свободного пробега электрона– это расстояние, которое проходит электрон между двумя последовательными столкновениями с ионами (u>> vср)
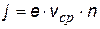(··)	плотность тока в проводнике; подставив в эту формулу вышеприведенные, получим:
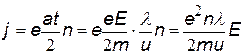	мы получили закон Ома в дифференциальной форме, запишем его в векторном виде:

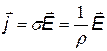	закон Ома в дифференциальной форме. В такой форме закон применим для бесконечно малого объема проводника, фактически – для точки проводника.
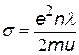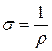(···)		s - удельная электропроводность проводника; r - удельное сопротивление проводника

Тема 8. Вопрос 3.

Часть 2.

Электронная теория проводимости металлов, несмотря на множество упрощающих предположений, позволяет теоретически вывести закон Ома и закон Джоуля – Ленца (см. ниже). Это свидетельствует о том, что модель поведения электронов в металле соответствует действительности. Вместе с тем эта теория столкнулась с рядом трудностей. Рассмотрим некоторые из них.

1)Теплоемкость металла теоретически должно складываться из теплоемкости кристаллической решетки и теплоемкости электронов: С_Ме = С_реш +С_элнов=

6R/2 + 3R/2 (для моля). Но из опыта следует, что теплоемкость почти всех твердых тел равна 3R. Таким образом, получается, что электроны не участвуют в теплоемкости, т.е. не «принимают» тепло при нагревании вещества. В дальнейшем с развитием квантовой механики выяснилось, что электроны в металле могут иметь не любые энергии, а только те, значения которых лежат в разрешенных зонах (см. III часть курса).

2)В формуле 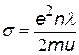e,m известны, n, u – можно вычислить, а s = 1/r измерить опытным путем. Таким образом можно оценить длину свободного пробега электрона l. Она оказалась равной порядка 10^-5 см, тогда как расстояние между ионами примерно 10^-8 см. Получается, что электрон пролетает мимо сотен ионов, не сталкиваясь с ними. Это затруднение также объяснила квантовая механика: движение электрона в металле – это распространение некоторой волны, искажение этой волны происходит на примесях (чужеродных атомах), а их металле значительно меньше, чем атомов решетки.

3)Затруднение возникло также с зависимостью сопротивления от температуры. Из 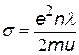следует, что удельное сопротивление r =1/s ~ 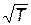, т.к. скорость теплового движения u ~ 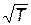, а остальные величины практически не зависят от температуры. Но из опыта следовало, что r ~ Т. Квантовая механика разрешила и это затруднение.

Тема 8. Вопрос 4.

Закон Джоуля – Ленца: «Если по проводнику протекает ток, в проводнике выделяется теплота Q». Найдем выражение для Q. Сначала получим закон в дифференциальной форме на основе электронной теории. Введем новое понятие:

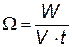(Дж/м3×с)

удельная мощность – это энергия, выделяющаяся в единице объема проводника за единицу времени

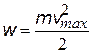	энергия, передаваемая одним электроном иону решетки за одно столкновение, т.е. за время t - время между двумя столкновениями.
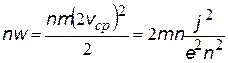	энергия, передаваемая электронами, находящимися в единице объема проводника за одно столкновение (за время t), n- концентрация электронов
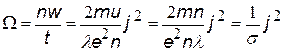	энергия, выделяющаяся в единице объема за единицу времени (формулы - см. закон Ома)

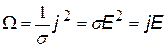закон Джоуля – Ленца в дифференциальной форме

Чтобы найти количество теплоты, выделяющейся во всем проводнике за некоторое время нужно проинтегрировать и использовать закон Ома: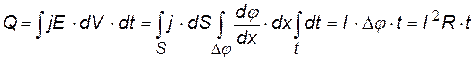

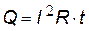	закон Джоуля - Ленца в интегральной форме	при постоянной силе тока, R – общее сопротивление участка цепи
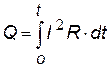	для случая, когда сила тока зависит от времени

Тема 8. Вопрос 5.