Аппроксимация и интерполяция данных
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПРИБОРОСТРОЕНИЯ И ИНФОРМАТИКИ
Пышный В.М.
Дисциплина:
’’ Компьютерные технологии в приборостроении’’
Методические рекомендации
по выполнению домашних работ
(для студентов специальности 200101)
Москва 2013г.
Рекомендовано к изданию редакционно-издательским советом МГУПИ в качестве методических рекомендаций по выполнению домашних работ.
Рецензент: д.т.н., профессор Слепцов В.В.
Пышный В.М.
Компьютерные технологии в приборостроении: методические рекомендации по выполнению домашних работ для студентов специальности 200101: – М.: МГУПИ, 2013. – с. 67.
Таб.16. Ил. 28. Библиограф.: 6 назв.
Методические указания по выполнению трех домашних работ предназначены для студентов 4-го семестра обучения и разработаны в соответствии с Государственными стандартами специальности 200100 «Приборостроение».
Домашние занятия по дисциплине "Компьютерные технологии в приборостроении" предназначены для углубления и закрепления теоретических знаний, полученных студентами на различных видах занятий и в процессе самостоятельного изучения учебного материала, приобретения ими навыков работы в среде Matlab и Simulink, а также совершенствование навыков работы с вычислительной техникой.
© Пышный В.М., 2013
© МГУПИ, 2013
Содержание………………………………………………………………………………3
Введение………………………………………………………………………………….5
1 Графический интерфейс пользователя Matlab……………………………………….5
1.1 Структура окна Command Window…………………………………………………6
1.2 Браузер рабочей области - окно Workspace………………………………………..8
1.3 Интерфейс редактора m-файлов…………………………………………………….9
2 Решение типовых задач алгебры и анализа в Matlab……………………………..11
2.1 Решение систем линейных уравнений………………………………………….11
2.2 Решение задачи Коши для систем обыкновенных дифференциальных уравнений (ОДУ)ode23, ode45…………………………………………………………………….13
2.3 Интегрирование методом трапецийtrapz…………………………………………15
2.4 Вычисление интегралов методом квадратурquad, quad 8……………………….16
2.5 Аппроксимация и интерполяция данных………………………………………….17
2.5.1 Кубическая интерполяция функции одной переменнойicubic………………...18
2.5.2 Интерполяция функции одной переменной кубическим сплайномspline…….19
2.5.3 Одномерная табличная интерполяцияinterp 1…………………………………..20
2.5.4 Аппроксимация периодической функции на основе быстрого преобразования Фурьеinterpft…………………………………………………………………………….21
3 Решение типовых задач алгебры и анализа в символьной форме………………23
3.1 Обозначения символьных переменных………………………………………….23
3.2 Вычисление пределов функций limit……………………………………………….23
3.3 Решение алгебраических уравнений и систем solve………………………………24
3.4 Дифференцирование функций diff………………………………………………….25
3.5 Решение дифференциальных уравнений в символьном виде dsolve……………..26
3.6 Интегрирование функции одной переменной int………………………………….26
4 Модели линейных динамических систем…………………………………………….27
4.1 Описание линейных динамических систем………………………………………...27
5 Выполнение анализа динамической системы в среде Matlab……………………….41
6 Создание моделей в среде Simulink………………………………………………….44
7 Моделирование линейной системы в пакете Simulink...……………………………51
7.1 Описание линейной системы………………………………………………………51
7.2 Выполнение анализа линейной динамической системы в среде Simulink……...52
8 Порядок выполнения домашних работ…………………………………………...54
8.1 Порядок выполнения домашней работы № 1…………………………………..55
8.2 Порядок выполнения домашней работы № 2…………………………………..55
8.3 Порядок выполнения домашней работы № 3…………………………………..55
9 Варианты заданий для выполнения домашних работ……………………………55
Список литературы……………………………………………………………………...65
Приложение А Пример обложки для оформления задания…………………………..66
Введение
Matlab - это высокопроизводительный язык для технических расчетов. Он включает в себя вычисления, визуализацию и программирование в удобной среде, где задачи и решения выражаются в форме, близкой к математической. Типичное использование Matlab - это:
- математические вычисления;
- создание алгоритмов;
- моделирование;
- анализ данных, исследования и визуализация;
- научная и инженерная графика;
- разработка приложений, включая создание графического интерфейса.
1 Графический интерфейс пользователя Matlab
Графический интерфейс пользователя Matlab состоит из 4-х независимых окон, имеющих следующие названия: Workspace, Command Window, Command History, Current Director (Рисунок 1)
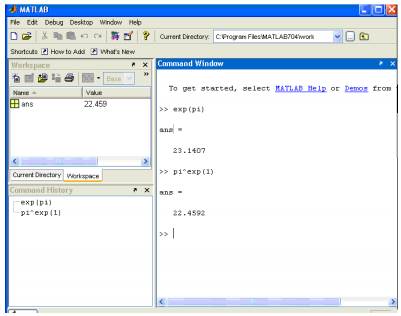
Рисунок 1 – Графический интерфейс пользователя Matlab
Окно Workspace (браузер рабочей области) используется для отображения состояния зарезервированной области памяти компьютера, в которой хранятся переменные, используемые в данном сеансе работы.
Окно Command Window является основным окном, в котором вводятся исполняемые команды и отображаются результаты вычислений.
Окно Command History используется для отображения содержимого буфера, в котором хранятся выполненные ранее команды пакета.
В окне Current Directory отображается список файлов и вложенных папок активного в данный момент каталога.
Для управления окнами используются стандартные средства операционной системы Windows. Для закрытия окон, отображение которых представляется пользователю в данный момент нецелесообразным, используется команды меню View.
1.1 Структура окна Command Window
После запуска Matlab на экране монитора мы видим окно Command Window (главное окно), содержащее: меню, инструментальную линейку с кнопками, клиентскую часть окна со знаком приглашения. Это окно обычно называется командное окно системы Matlab, его структура аналогична структуре Windows - приложений (Рисунок 2). Здесь происходят вычисления, и мы видим приглашение >>.
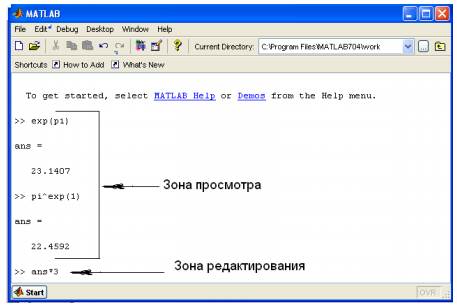
Рисунок 2 – Структура командного окна Matlab
Исправление информации в зоне просмотра невозможно. В зоне просмотра, можно с помощью мыши выделить любой фрагмент текста, затем скопировать его в буфер обмена операционной системы Windows, затем вставить данный фрагмент в командную строку Matlab или документ, созданный в каком-либо приложении, работающем под управлением операционной системы Windows.
Сеанс работы с Matlab принято называть сессией (session). Сессия - это текущий документ, отражающий работу пользователя с системой. В ней имеются строки ввода, вывода, сообщения об ошибках. Входящие в сессию определения переменных и функций, расположенные в рабочей области памяти (но не саму сессию) можно записать на диск (файлы с расширением mat), используя команду Save.
В некоторых случаях вводимое математическое выражение может оказаться настолько длинным, что для него не хватит одной строки. В этом случае часть выражения можно перенести на новую строку с помощью знака многоточия то есть три или более точек (Рисунок 3).
Исправление информации в зоне просмотра невозможно. В зоне просмотра, можно с помощью мыши выделить любой фрагмент текста, затем скопировать его в буфер обмена операционной системы Windows, затем вставить данный фрагмент в командную строку Matlab или документ, созданный в каком-либо приложении, работающем под управлением операционной системы Windows.
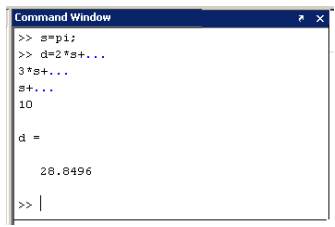
Рисунок 3 – Ввод команды, размещающейся на нескольких строках
Очистка командного окна Matlab осуществляется командой clc, которая, однако, оставляет неизменным содержимое буфера команд и рабочего пространства Matlab. Действительно, если после этого набрать имя ранее вычисленной переменной d, то после нажатия клавиши ENTER мы снова увидим ее значение:
>> d
d =
28 . 8496
1.2 Браузер рабочей области - окно Workspace
Значения переменных, вычисленных в течение текущего сеанса работы, сохраняются в специально зарезервированной области оперативной памяти компьютера, называемой рабочим пространством Matlab (браузером рабочей области Matlab - окно Workspace). (Рисунок 4).
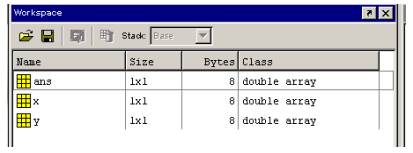
Рисунок 4 – Окно просмотра рабочей области памяти
Браузер рабочей области служит для просмотра рабочей области памяти. Для вызова браузера в командном окне надо набрать: Desktop/ Workspase.
Возможности браузера
Браузер позволяет:
- просмотреть существующие в памяти объекты;
- редактировать их содержимое;
- удалять объекты из памяти, т.к. матрицы и графики могут занимать многие мегабайты (выделить нужное и delete);
- векторы и матрицы могут занимать большой объем памяти, цветные изображения с высоким разрешением, могут занимать в памяти объем, исчисляемый многими мегабайтами, и в этом случае оценка их размера становится необходимой.
Для вывода содержимого объекта достаточно выделить его имя с помощью мыши и щелкнуть па кнопке Open. Объект можно открыть и двойным щелчком на его имени в списке. Кнопка Delete уничтожает объект с заданным именем и удаляет его из памяти, а кнопка Close закрывает окно просмотра.
Окно Array Editor
Из окна Workspase двойным щелчком левой кнопки мыши по строке, содержащей имя переменной, можно вызвать окно Array Editor, в котором можно просматривать и менять значения выбранной переменной. Для примера на рисунке 5 показано соответствующее окно, появившееся после двойного клика по строке, содержащей имя переменной а.
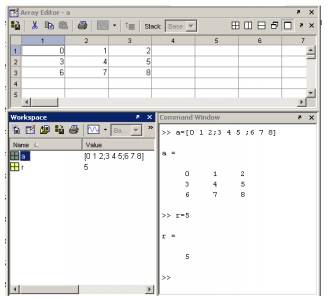
Рисунок 5 – Три окна Command Window, Workspace, Array Editor
1.3 Интерфейс редактора m-файлов
Для подготовки, редактирования и отладки m-файлов служит специальный многооконный редактор. Он выполнен как типичное приложение Windows (Рисунок 6). Редактор m-файлов можно вызывать командой Edit из командной строки или командой File/ New/ M-file
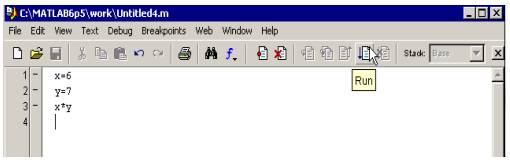
Рисунок 6 – Интерфейс редактора m-файлов
После этого в окне редактора можно:
- создавать и сохранять свой файл, используя команду Save As меню File редактора;
- пользоваться средствами его отладки и запускать свой файл командой Run.
На первый взгляд может показаться, что редактор/отладчик - просто лишнее звено в цепочке «пользователь - Matlab». И в самом деле, текст файла можно было бы ввести в окно системы и получить тот же результат.
Однако на деле редактор/отладчик выполняет важную роль. Он позволяет создать m-файл (программу) без того многочисленного вывода информации, которая сопровождает работу в командном режиме. Редактор обеспечивает синтаксический контроль файла.
Редактор имеет и другие важные отладочные средства:
- он позволяет устанавливать в тексте файла специальные метки, именуемые точками прерывания (останова). При их достижении вычисления приостанавливаются, и пользователь может оценить промежуточные результаты вычислений (например, значения переменных), проверить правильность выполнения циклов и т. д.;
- редактор позволяет записать файл в текстовом формате и сохранить ваш файл.
Для отображения имен переменных, размещенных в данный момент в рабочем пространстве, нужно выполнить команду who.
Данная команда отображает в рабочем окне список всех переменных, находящихся в рабочем пространстве Matlab. Выполнив команды, представленные на рисунок 6, и далее команду
>> who
получим Your variables are: х у >>
После завершения сеанса работы с Matlab все ранее вычисленные переменные теряются. Для сохранения в файле на диске компьютера содержимого рабочего пространства, нужно выполнить команду меню
File/ Save Workspace as...
После чего появляется стандартное диалоговое окно операционной системы Windows для выбора каталога на диске и имени файла. Для файлов, в которых Matlab сохраняет значения переменных из рабочего пространства нужно использоваться расширение mat, поэтому такие файлы принято называть «mat-файлами».
Редактор/отладчик m-файлов выполняет синтаксический контроль программного кода по мере ввода текста. При этом используются следующие цветовые выделения:
- ключевые слова языка программирования - синий цвет;
- операторы, константы и переменные - черный цвет;
- комментарии после знака % - зеленый цвет;
- символьные переменные (в апострофах) - зеленый цвет;
- синтаксические ошибки - красный цвет.
Благодаря цветовым выделениям вероятность синтаксических ошибок резко снижается. Однако далеко не все ошибки диагностируются. Ошибки, связанные с неверным применением операторов или функций (например, применение оператора - вместо + или функции cos(x) вместо sin(x) и т. д.), не способна обнаружить ни одна система программирования.
2 Решение типовых задач алгебры и анализа в Matlab
2.1 Решение систем линейных уравнений
В системе Matlab для решения систем линейных уравнений предусмотрены знаки операций / и \. Чтобы решить систему линейных уравнений вида:
A⋅ X= B, (1)
где A – заданная квадратная матрица размером NxN, a B – заданный вектор –
столбец длины N, достаточно применить операцию \ и вычислить выражение A \ B. Операция \ называется левым делением матриц и, будучи примененная к матрицам A и B в виде A \ B , примерно эквивалентна вычислению выражения:
inv( A) * B (2)
Здесь под inv( A) понимается вычисление матрицы, обратной к матрице A . Операцию / называют правым делением матрицы. Выражение A / B примерно соответствует вычислению выражения B * inv( A) . Значит, эта операция позволяет решать системы линейных уравнений вида (1)
Для задачи решения системы линейных алгебраических уравнений,одной из популярнейших в вычислительной математике, предусмотрены даже “элементарные” операции для подобной задачи. Так для решения системы A⋅ X=B (A – матрица коэффициентов размерности m´n, B- матрица правых частей размерности n´k, Х – матрица из k векторов- столбцов решений) можно использовать команду обратного деления “\”. Например, для решения системы:
x1+2 x2+3 x3= 3
5 x1+4 x2+3 x3= 9 (3)
3 x1+4 x2+3 x3= 6
задаем (построчно) матрицу коэффициентов и векторов правой части
» A=[1 2 3; 5 4 3; 3 4 3]
» B=[3 3; 9 9; 6 7]
и выполнить
» X=A\B
X = 1.5000 1.0000
0.0000 1.0000
0.5000 0.0000
2.2 Решение задачи Коши для систем обыкновенных дифференциальных уравнений (ОДУ)ode23, ode45
Синтаксис:
[t, X] = ode23(‘<имя функции>‘, t0, tf, x0)
[t, X] = ode23(‘<имя функции>‘, t0, tf, x0, tol, trace)
[t, X] = ode45(‘<имя функции>‘, t0, tf, x0)
[t, X] = ode45(‘<имя функции>‘, t0, tf, x0, tol, trace)
Описание:
Функции ode23 и ode45 предназначены для численного интегрирования систем ОДУ. Они применимы как для решения простых дифференциальных уравнений, так и для моделирования сложных динамических систем. Любая система нелинейных ОДУ может быть представлена как система дифференциальных уравнений 1-го порядка в явной форме Коши:
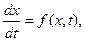 (4)
(4)
где x - вектор состояния;
t - время;
f - нелинейная вектор-функция от переменных x, t.
Функции [t, X] = ode23(‘<имя функции>‘, t0, tf, x0, tol, trace) и [t, X] = = ode45(‘<имя функции>‘, t0, tf, x0, tol, trace) интегрируют системы ОДУ, используя формулы Рунге - Кутта соответственно 2-го и 3-го или 4-го и 5-го порядка.
Эти функции имеют следующие параметры:
Входные параметры:
‘<имя функции>‘ - строковая переменная, являющаяся именем m-файла, в котором вычисляются правые части системы ОДУ;
t0 - начальное значение времени; tfinal - конечное значение времени;
x0 - вектор начальных условий;
tol - задаваемая точность; по умолчанию для ode23 tol = 1.e-3, для ode45 tol = 1.e-6);
trace - флаг, регулирующий вывод промежуточных результатов; по умолчанию равен нулю, что подавляет вывод промежуточных результатов;
Выходные параметры:
t - текущее время;
X - двумерный массив, где каждый столбец соответствует одной переменной.
Пример:
Рассмотрим дифференциальное уравнение 2-го порядка, известное как уравнение Вандер Поля:


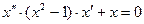 (5)
(5)
Это уравнение может быть представлено в виде системы ОДУ в явной форме Коши:
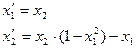 (6)
(6)
Первый шаг процедуры интегрирования - это создание m-файла для вычисления правых частей ОДУ; присвоим этому файлу имя vdpol.
function xdot = vdpol(t, x)
xdot = [x(2); x(2) .* (1 - x(1).^2) - x(1)];
Чтобы проинтегрировать систему ОДУ, определяемых функцией vdpol в интервале времени 0 <= t <= 20, вызовем функцию ode23:
t0 = 0; tf = 20;
x0 = [0 0.25]'; % Начальные условия
[t, X] = ode23('vdpol', t0, tf, x0);
plot(t, X), grid, hold on
gtext('x1'), gtext('x2')
Результаты решения дифференциальных уравнений представлены на рисунке 7
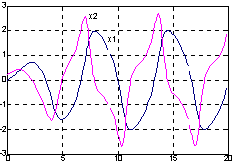
Рисунок 7 - Результаты решения дифференциальных уравнений
Функции ode23 и ode45 реализуют методы Рунге - Кутта с автоматическим выбором шага. Такие алгоритмы используют тем большее количество шагов, чем медленнее изменяется функция. Поскольку функция ode45 использует формулы более высокого порядка, обычно требуется меньше шагов интегрирования и результат достигается быстрее. Для сглаживания полученных процессов можно использовать функцию interp1.
2.3 Интегрирование методом трапецийtrapz
Синтаксис:
I = trapz(x, y)
I = trapz(y)
Описание:
Функция I = trapz(x, y) вычисляет интеграл от функции y по переменной x, используя метод трапеций. Аргументы x и y могут быть одномерными массивами одинакового размера, либо массив Y может быть двумерным, но тогда должно выполняться условие size(Y, 1) = length(x). В последнем случае вычисляется интеграл для каждого столбца. Функция I = trapz(y) вычисляет интеграл, предполагая, что шаг интегрирования постоянен и равен единице; в случае, когда шаг h отличен от единице, но постоянен, достаточно вычисленный интеграл умножить на h.
Примеры:
Вычислим интеграл
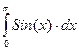 (7)
(7)
Его точное значение равно двум.
Выберем равномерную сетку
x = 0:pi/100:pi; y = sin(x);
тогда оба интеграла
I = trapz(x, y) и I = pi/100*trapz(y)
дают одинаковый результат:
I = 1.9998.
2.4 Вычисление интегралов методом квадратурquad, quad8
Функция quad использует квадратурные формулы Ньютона - Котеса 2-го порядка (правило Симпсона), а функция quad8 - формулы 8-го порядка
Квадратура - это численный метод вычисления площади под графиком функции, то есть вычисление определенного интеграла вида (7)
Синтаксис:
[I, cnt] = quad(‘<имя функции>‘, a, b)
[I, cnt] = quad(‘<имя функции>‘, a, b, tol)
[I, cnt] = quad(‘<имя функции>‘, a, b, tol, trace)
[I, cnt] = quad8(‘<имя функции>‘, a, b)
[I, cnt] = quad8(‘<имя функции>‘, a, b, tol)
[I, cnt] = quad8(‘<имя функции>‘, a, b, tol, trace)
Описание:
Функции quad и quad8 используют разные квадратурные формулы.
Функции [I, cnt] = quad(‘<имя функции>‘, a, b) и [I, cnt] = quad8(‘<имя функции>‘, a, b) вычисляют интеграл от заданной функции; последняя может быть как встроенной функцией, так и М-файлом. Переменная cnt содержит информацию о том, сколько раз в процессе интегрирования вычислялась подынтегральная функция.
Функции [I, cnt] = quad(‘<имя функции>‘, a, b, tol) и [I, cnt] = quad8(‘<имя функции>‘, a, b, tol) вычисляют интеграл с заданной относительной погрешностью tol. По умолчанию tol = 1e-3.
Функции [I, cnt] = quad(‘<имя функции>‘, a, b, tol, trace) и [I, cnt] = quad8 (‘<имя функции>‘, a, b, tol, trace), когда аргумент trace не равен нулю, строят график, показывающий ход вычисления интеграла.
Пример:
Вычислим интеграл заданный формулой 7.
Его точное значение равно двум.
[I, cnt] = quad('sin', 0, pi) [I, cnt] = quad('sin', 0, pi, 1e-4, 1)
I = 2.0000 I = 2.0000
cnt = 17 cnt = 33
Аппроксимация и интерполяция данных
При аппроксимации и интерполяция данных в Matlab применяются следующие основные методы:
icubic - кубическая интерполяция функции одной переменной;
spline - интерполяция функции одной переменной кубическим сплайном;
interp1 - одномерная табличная интерполяция;
interp2 - двумерная табличная интерполяция;
interpft - аппроксимация периодической функции на основе быстрого преобразования Фурье.
Эти методы применимы для табличных данных и функций, в последнем случае таблица данных вычисляется.
2.5.1 Кубическая интерполяция функции одной переменнойicubic
Синтаксис:
yi = icubic(y, xi)
yi = icubic(x, y, xi)
Описание:
Функция yi = icubic(y, xi) интерполирует значения функции y в точках xi внутри области определения функции, используя кубические полиномы. Если Y - двумерный массив, то интерполирующая кривая строится для каждого столбца. Если указано значение xi вне области определения функции, то результатом будет NaN.
Функция yi = icubic(x, y, xi) позволяет использовать более мелкую сетку xi при условии, что аргумент x изменяется монотонно и сетка равномерна.
Пример:
Зададим синусоиду всего 10 точками и проведем интерполяцию, используя мелкую сетку.
x = 0:10; y = sin(x);
xi = 0:.25:10;
yi = icubic(x, y, xi);
plot(x, y, 'o', xi, yi, ‘g’), grid.
Результат кубической интерполяции представлен на рисунке 8
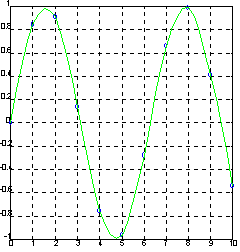
Рисунок 8 - Результат кубической интерполяции
2.5.2 Интерполяция функции одной переменной кубическим сплайномspline
Синтаксис:
yi = spline(x, y, xi)
pp = spline(x, y)
v = ppval(pp, xx)
[breaks, coefs, l, k] = unmkpp(pp)
pp = mkpp(breaks, coefs)
Описание:
Функция yi = spline(x, y, xi) интерполирует значения функции y в точках xi внутри области определения функции, используя кубические сплайны.
Функция pp = spline(x, y) возвращает pp-форму сплайна, используемую в m-файлах ppval, mkpp, unmkpp. Функция v = ppval(pp, xx) вычисляет значение кусочно-гладкого полинома pp для значений аргумента xx.
Функция [breaks, coefs, l, k] = unmkpp(pp) возвращает характеристики кусочно гладкого полинома pp:
breaks - вектор разбиения аргумента;
coefs - коэффициенты кубических сплайнов;
l = length(breaks) - 1;
k = length(coefs)/l.
Функция pp = mkpp(breaks, coefs) формирует кусочно-гладкий полином pp по его характеристикам.
Пример:
Зададим синусоиду всего 10 точками и проведем интерполяцию кубическими сплайнами, используя мелкую сетку.
x = 0:10; y = sin(x);
xi = 0:.25:10;
yi = spline(x, y, xi);
plot(x, y, 'o', xi, yi, ‘g’), grid
Результат интерполяции кубическим сплайном представлен на рисунке 9
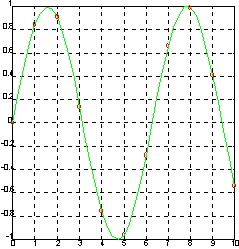
Рисунок 9 - Результат интерполяции кубическим сплайном
2.5.3 Одномерная табличная интерполяцияinterp1
Синтаксис:
yi = interp1(x, y, xi)
yi = interp1(x, y, xi, ‘<метод>‘)
Описание:
Функция yi = interp1(x, y, xi) строит интерполирующую кривую для одномерного массива y, заданного на сетке x; выходной массив yi может быть определен на более мелкой сетке xi. Если Y - двумерный массив, то интерполирующая кривая строится для каждого столбца. По умолчанию реализована линейная интерполяция.
Функция yi = interp1(x, y, xi, ‘<метод>‘) позволяет задать метод интерполяции:
‘linear’ линейная
‘cubic’ кубическая
‘spline’ кубические сплайны
Принято, что аргумент x изменяется монотонно; кроме того, для кубической интерполяции предполагается, что сетка по x равномерна.
Пример:
Зададим синусоиду всего 10 точками и проведем интерполяцию, используя мелкую сетку.
x = 0:10; y = sin(x);
xi = 0:.25:10;
yi = interp1(x, y, xi);
plot(x, y, 'o', xi, yi, ‘g’), hold on
yi = interp1(x, y, xi, ‘spline’ );
plot(x, y, 'ob', xi, yi, ‘m’), grid, hold off
Результат одномерной табличной интерполяции представлен на рисунке 10
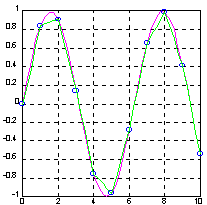
Рисунок 10 - Результат одномерной табличной интерполяции
2.5.4 Аппроксимация периодической функции на основе быстрого преобразования Фурьеinterpft
Синтаксис:
yp = interpft(y, n)
Описание:
Функция yp = interpft(y, n) возвращает одномерный массив чисел, который является периодической функцией, определенной в n точках и аппроксимирующей одномерный массив y. Если length(x) = m, а интервал дискретности dx, то интервал дискретности для y определяется по формуле dy = dx * m/n, причем n всегда превышает m.
Пример:
Рассмотрим аппроксимацию функции y = sin(x), которая задана 11 точками на интервале [0 10].
x = 0:10; y = sin(x);
xp = 0:0.25:10;
yp = interpft(y, 41);
xt = 0:0.01:10; yt = sin(xt);
plot(xt, yt, 'r'), hold on, plot(x, y, 'ob', xp, yp)
Результат аппроксимация периодической функции на основе быстрого преобразования Фурьепредставлен на рисунке 11
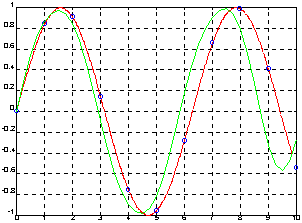
Рисунок 11 - Результат аппроксимация функции на основе преобразования Фурье
На графике построена точная функция y = sin(x) с указанием точек съема данных и ее аппроксимация в 41 точке. Как видно из графика, аппроксимация вне интервала [0 1.5] имеет нарастающую погрешность.
3 Решение типовых задач алгебры и анализа в символьной форме
3.1 Обозначения символьных переменных
Под символьным объектом в системе Matlab понимается переменная, предназначенная для символьных преобразований. Объявление такой переменной осуществляется функцией sym либо syms.
Функция syms позволяет объявлять сразу несколько символьных переменных, которые необходимо отделять друг от друга пробелами, например:
» syms x y z;
Функция sym используется при объявлении какой-либо одной переменной символьной, например:
x = sym('x'); y = sym('y'); z = sym('z');
объявление символьных переменных х, y, z.
3.2 Вычисление пределов функций limit
Вычисление пределов от символьных выражений производится с помощью встроенной функции limit. Соответствие между традиционным математическим описанием и символьным системы Matlab приводится в таблице 1.
Таблица 1 – Вычисления пределов
| Традиционное математическое действие | Команда MATLAB |
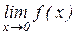 | 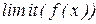 |
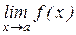 | 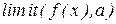 |
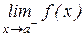 | 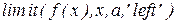 % предел слева % предел слева |
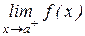 | 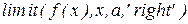 % предел справа % предел справа |
Примечание: символ бесконечность ( 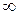 ) в Matlab записывается как inf. Неопределенное значение в Matlab записывается какNaN.
) в Matlab записывается как inf. Неопределенное значение в Matlab записывается какNaN.
Пример: Вычислить предел выражения 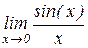 :
:
» syms x
» y1=sin(x)/x;
» limit(y1)
ans =
1 % Предел отношения равен единицы
