| Задание | Комментарии | Ответ |
| Блок 1. (обязательный минимум-подготовка к задачам ЕГЭ) |
| 1. Сколькими нулями оканчивается число 400! ? | Перебираем двойки и пятерки в разложении на множители. Понятно, что двоек гораздо больше. Значит, для каждой двойки найдется пятерка! Считаем пятерки. Внимательно! Ведь есть числа. Которые делятся не только на 5, а на 25 и даже 125. Их количество ( с учетом делимости на степень пятерки) и дает ответ. | |
2. При каких натуральных значениях 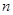 дробь дробь 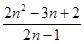 есть целое число? есть целое число? | Делим с остатком числитель на знаменатель, то есть выделяем целую часть дроби. Дробь равна целому числу плюс «число, деленное на 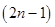 ». Остается выяснить, на какие целые числа делится число, то есть какие значения может принимать ». Остается выяснить, на какие целые числа делится число, то есть какие значения может принимать 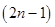 , при каких , при каких 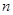 это происходит, и какие их них натуральные. это происходит, и какие их них натуральные. | |
3. Решите в целых числах уравнение 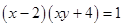 | Единица из правой части раскладывается в произведение двух целых множителей не таким уж большим количеством способов…. Всего-то двумя! (1,1 и -1,-1). Получаем две системы (для каждого из случаев – по одной). Находим ответ. | 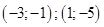 |
4. Решите в целых числах уравнение 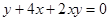 . . | Задача полностью сводится к предыдущей, только надо это увидеть. Добавим в каждую часть уравнения по 2, и левая часть разложится на множители! Правда, решать придется уже не две системы, а 4: множители 2,1; 1,2; -2,-1; -1,-2. | 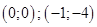 |
5. Решите в целых числах уравнение 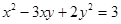 . . | Однородное выражение в левой части раскладывается на множители стандартным образом (например, как квадратный трехчлен относительно 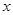 ). Перебираем разложения тройки. ). Перебираем разложения тройки. | 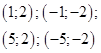 |
6. Докажите, что уравнение 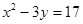 не имеет решений в целых числах. не имеет решений в целых числах. | Квадрат целого числа не может давать при делении на 3 остаток 2. (Докажите, перебрав все три возможных остатка при делении на 3 числа, возводимого в квадрат.) | |
| 7. Найдите общий вид таких чисел, которые при делении на 5 дают остаток 2, а при делении на 3 – остаток 1. | Записываем уравнение в целых числах: 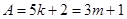 ,далее возможны варианты. 1) просто перебираем остатки при делении А на 15 - НОК(3;5). 2) приводим подобные; перебираем все остатки при делении ,далее возможны варианты. 1) просто перебираем остатки при делении А на 15 - НОК(3;5). 2) приводим подобные; перебираем все остатки при делении  на 3 (можно при делении на 3 (можно при делении  на 5, но это дольше). Ищем, в каком случае возможно равенство, подставляем в выражение для А соответствующий вид на 5, но это дольше). Ищем, в каком случае возможно равенство, подставляем в выражение для А соответствующий вид 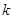 : : 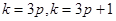 или или 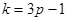 . Получаем ответ. 3) представляем свободный член – число 1- в виде суммы некоторого количества троек и пятерок, например, . Получаем ответ. 3) представляем свободный член – число 1- в виде суммы некоторого количества троек и пятерок, например, 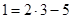 . Далее переносим все «тройки» в одну часть уравнения, все «пятерки» - в другую, и делаем вывод о делимости обеих частей, например, на 3. Получаем общий вид числа . Далее переносим все «тройки» в одну часть уравнения, все «пятерки» - в другую, и делаем вывод о делимости обеих частей, например, на 3. Получаем общий вид числа 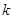 . Так, пожалуй, быстрее всего. . Так, пожалуй, быстрее всего. | 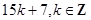 |
8. Докажите, что при любом целом 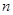 число число 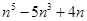 делится на 120. делится на 120. | Раскладываем на множители. Произведение пяти последовательных целых чисел должно делиться на 5!=120. | |
9. Решите в натуральных числах уравнение 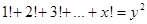 . . | Если 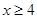 , то левая часть уравнения оканчивается на 3 ( так как факториалы чисел , больших 4, содержат множители 5 и 2, то есть оканчиваются 0). Квадрат же не может заканчиваться тройкой. Перебираем , то левая часть уравнения оканчивается на 3 ( так как факториалы чисел , больших 4, содержат множители 5 и 2, то есть оканчиваются 0). Квадрат же не может заканчиваться тройкой. Перебираем 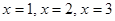 . . | 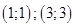 |
10. Решите в простых числах уравнение 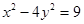 . . | Либо левую часть представляем как разность квадратов и перебираем разложения 9 на множители, либо переносим 9 влево, а 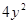 - вправо; тогда - вправо; тогда 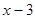 и и 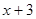 (одной четности) – четные числа, отличающиеся на 6, то есть одно из них делится не только на 2, но и на 4. Следовательно, (одной четности) – четные числа, отличающиеся на 6, то есть одно из них делится не только на 2, но и на 4. Следовательно, 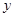 - четное простое число, то есть 2. - четное простое число, то есть 2. | 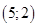 |
| Блок 2. (задания уровня ЕГЭ) |
11. Найдите все простые числа 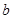 , для каждого из которых существует такое целое число , для каждого из которых существует такое целое число 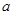 , что дробь , что дробь 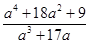 сократима на сократима на 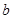 . . | Кроме числителя и знаменателя, можно найти еще числа, делящиеся на 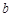 . Поиском занимаемся, либо подгадывая такие комбинации исходных чисел, чтобы степени уменьшались (а в конце получаем число, которое точно делится на . Поиском занимаемся, либо подгадывая такие комбинации исходных чисел, чтобы степени уменьшались (а в конце получаем число, которое точно делится на 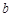 ), либо с использованием деления с остатком ( сродни алгоритму Евклида). ), либо с использованием деления с остатком ( сродни алгоритму Евклида). | 2,3 |
12. Найдите все такие простые числа p, для каждого из которых существует такое целое число k, что число p является общим делителем чисел 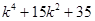 и и 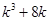 . . | Задача аналогична предыдущей. | 3, 5, 7. |
13. Наибольшее целое число, не превосходящее 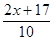 , равно , равно 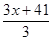 . Найдите все такие действительные значения . Найдите все такие действительные значения 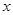 . . | Записываем условие-ограничение, получаем неравенство на 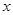 . Решаем. Далее замечаем, что . Решаем. Далее замечаем, что 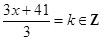 ; выражаем ; выражаем 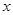 через через 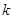 , подставляем в полученное решение неравенства. Выбираем наибольшее целое , подставляем в полученное решение неравенства. Выбираем наибольшее целое 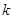 . Находим . Находим 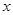 , пишем в ответ. , пишем в ответ. | 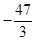 |
14. Найдите все натуральные числа 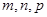 , для которых верно равенство , для которых верно равенство 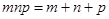 . . | Возможны различные рассуждения при решении этой задачи, и мы ни в коем случае не претендуем на уникальность или оптимальность решения. Предложим один из вариантов. Используем ограничения, которые очень легко получить, зная, что переменные – натуральные числа, то есть не меньше 1. Далее получаем конечный (да и небольшой) набор возможных значений одной из переменных, и задача сводится к трем стандартным уравнениям в целых числах. Иногда в подобных задачах для получения ограничений приходится использовать базовые неравенства. | 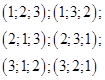 |
15. Найдите все целые значения 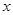 и и 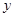 , для которых выполняется равенство , для которых выполняется равенство 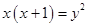 . . | Если раскрыть скобки и использовать разложение на множители, то получим стандартное уравнение, решаемое конечным перебором. | 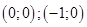 |
16. Решите в натуральных числах уравнение 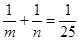 , где , где 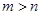 . . | Домножением на знаменатели сводим задачу к предыдущей. Есть другой способ решения, использующий то, что из двух положительных слагаемых в левой части должно быть одно, которое не менее половины правой части. Но со знаменателем 25 такое решение менее удобно. | 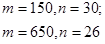 |
17. Решите в натуральных числах уравнение 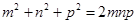 . . | Задача решается методом «бесконечного спуска». Рассматривается четность-нечетность входящих в условие переменных и делается обобщающий вывод. Фактически, задача неявно предполагает действия методом математической индукции. | Решений нет |
18. Решите в натуральных числах уравнение 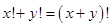 . . | Несложные рассуждения с делимостью, правда, на факториал, и аккуратность в конце приводят к ответу, довольно очевидному при взгляде на уравнение. Надо заметить, что здесь приходится упорядочить переменные, отдельно рассмотрев случай равенства. | 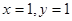 |
19. Найдите все тройки натуральных чисел 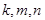 , удовлетворяющие уравнению , удовлетворяющие уравнению 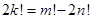 . . | Опять упорядочим переменные, проведем небольшую оценку и сведем все к конечному перебору. | 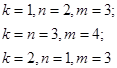 |
20. Решите в натуральных числах уравнение 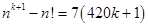 . . | В условии бросаются в глаза семерки в правой части. Точнее, на 7 она делится, а на 49 уже нет… Так что в связи с делимостью на 7 придется рассмотреть значения 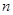 меньше 7 (перебрать легко, тем более если еще что-нибудь отсеять….) и не меньше 7 (здесь поработать с делимостью). меньше 7 (перебрать легко, тем более если еще что-нибудь отсеять….) и не меньше 7 (здесь поработать с делимостью). | 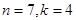 |
21. Найдите все пары натуральных чисел 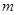 и и 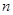 , являющиеся решениями уравнения , являющиеся решениями уравнения 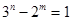 . . | Пара нетривиальных задач с коротким решением для наблюдательных людей. Надо хорошо знать свойства, связанные с четностью и со степенями 3….. Если вы угадаете, делимость на что надо рассматривать. То есть шанс решить задачу! | 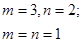 |
22. Найдите все пары натуральных чисел 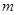 и и 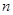 , являющиеся решениями уравнения , являющиеся решениями уравнения 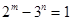 . . | 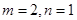 |
| 23. Винтики можно разложить в пакетики, а пакетики упаковать в коробки, по 3 пакетика в одну коробку. Можно эти же винтики разложить в пакетики так, что в каждом пакетике будет на 3 винтика больше, чем раньше, но тогда в каждой коробке будет лежать по 2 пакетика, а коробок потребуется на 2 больше. Какое наибольшее количество винтиков может быть при таких условиях? | Классическая текстовая задача на составление и решение уравнения в целых числах со смысловыми ограничениями. Внимательно читаем условие и вопрос задачи! | |
| 24. Перед каждым из чисел 2;3;…;6 и 10;11;…;20 произвольным образом ставят знак плюс или минус, после чего к каждому из образовавшихся чисел первого набора прибавляют каждое из образовавшихся чисел второго набора, а затем все 55 полученных результатов складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге? | На один из вопросов задачи ответить легко, если знать, как суммируется прогрессия, или потратить просто побольше времени на складывание чисел. (да, во второй задаче надо сначала заметить произведение двух скобок). Со вторым вопросом значительно сложнее. Надо сделать целых две вещи: первое – доказать, что 0 получиться не может(четность). Второе – привести пример, когда получается 1 (это тоже нетривиально, нужна фантазия). | 1 и 1045 |
| 25. Каждое из чисел 2;3;…;7 умножают на каждое из чисел 13; 14;…;21 и перед каждым из полученных произведений ставят знак плюс или минус, после чего все 54 полученных результата складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге? | 1 и 4131 |
| 26. Какое наибольшее число членов может иметь геометрическая прогрессия, все члены которой – различные натуральные числа, большие 210 и меньшие 350? | Логическая задача, включающая необходимость придумать пример, подтверждающий догадку об ответе, и обосновать, что ответ верный – то есть в нашем случае аккуратно доказать с помощью неравенств, что пяти членов уже быть не может. | |
27. Последние члены двух конечных арифметических прогрессий 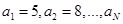 и и 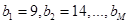 совпадают, а сумма всех совпадающих (взятых по одному разу) членов этих погрессий равна 815. Найдите число членов в каждой прогрессии. совпадают, а сумма всех совпадающих (взятых по одному разу) членов этих погрессий равна 815. Найдите число членов в каждой прогрессии. | Классическая задачка на совмещение двух прогрессий и постановку ограничений. Уравнение в целых числах. См.подготовительные задания. | 49 и 29 |
28. Найдите все пары натуральных чисел 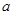 и и 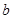 , удовлетворяющие равенству , удовлетворяющие равенству 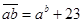 ( в левой части равенства стоит число, получаемое приписыванием десятичной записи числа ( в левой части равенства стоит число, получаемое приписыванием десятичной записи числа 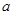 перед десятичной записью числа перед десятичной записью числа 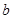 ) ) | . Оценка длины десятичной записи числа. Хитрое сведение к конечному перебору с помощью оценок. Выполните затем аналогичную задачу самостоятельно. | 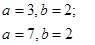 |
29. Число 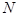 равно произведению 10 различных натуральных чисел, больших 1. Какое наименьшее число различных натуральных делителей (включая единицу и само число) может иметь число равно произведению 10 различных натуральных чисел, больших 1. Какое наименьшее число различных натуральных делителей (включая единицу и само число) может иметь число 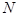 ? ? | Разумный перебор делителей, подсчет их количества, включающий расположение по возрастанию (упорядочение опять сильно помогает решению) не исчерпывают решение. Опять-таки надо привести пример того. Что оптимальное значение достижимо. | |
30. Сумма шестнадцати чисел равна 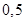 . Оказалось, что сумма каждых пятнадцати из этих шестнадцати чисел положительна. Какое наименьшее целое значение может иметь наименьшее из данных чисел? . Оказалось, что сумма каждых пятнадцати из этих шестнадцати чисел положительна. Какое наименьшее целое значение может иметь наименьшее из данных чисел? | НЕОБХОДИМО упорядочение чисел. Далее легкая, но красивая оценка нужного числа и, конечно, как же без примера реализации… Проделайте в домашней задаче все то же самое самостоятельно. | -6 |
| | | | |
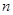 дробь
дробь 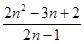 есть целое число?
есть целое число? 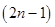 ». Остается выяснить, на какие целые числа делится число, то есть какие значения может принимать
». Остается выяснить, на какие целые числа делится число, то есть какие значения может принимать 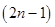 , при каких
, при каких 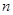 это происходит, и какие их них натуральные.
это происходит, и какие их них натуральные. 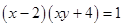
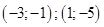
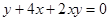 .
. 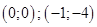
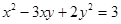 .
. 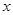 ). Перебираем разложения тройки.
). Перебираем разложения тройки. 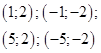
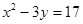 не имеет решений в целых числах.
не имеет решений в целых числах. 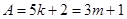 ,далее возможны варианты. 1) просто перебираем остатки при делении А на 15 - НОК(3;5). 2) приводим подобные; перебираем все остатки при делении
,далее возможны варианты. 1) просто перебираем остатки при делении А на 15 - НОК(3;5). 2) приводим подобные; перебираем все остатки при делении 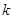 на 3 (можно при делении
на 3 (можно при делении 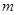 на 5, но это дольше). Ищем, в каком случае возможно равенство, подставляем в выражение для А соответствующий вид
на 5, но это дольше). Ищем, в каком случае возможно равенство, подставляем в выражение для А соответствующий вид 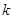 :
: 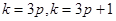 или
или 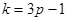 . Получаем ответ. 3) представляем свободный член – число 1- в виде суммы некоторого количества троек и пятерок, например,
. Получаем ответ. 3) представляем свободный член – число 1- в виде суммы некоторого количества троек и пятерок, например, 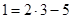 . Далее переносим все «тройки» в одну часть уравнения, все «пятерки» - в другую, и делаем вывод о делимости обеих частей, например, на 3. Получаем общий вид числа
. Далее переносим все «тройки» в одну часть уравнения, все «пятерки» - в другую, и делаем вывод о делимости обеих частей, например, на 3. Получаем общий вид числа 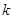 . Так, пожалуй, быстрее всего.
. Так, пожалуй, быстрее всего. 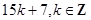
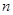 число
число 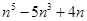 делится на 120.
делится на 120. 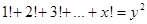 .
. 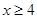 , то левая часть уравнения оканчивается на 3 ( так как факториалы чисел , больших 4, содержат множители 5 и 2, то есть оканчиваются 0). Квадрат же не может заканчиваться тройкой. Перебираем
, то левая часть уравнения оканчивается на 3 ( так как факториалы чисел , больших 4, содержат множители 5 и 2, то есть оканчиваются 0). Квадрат же не может заканчиваться тройкой. Перебираем 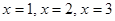 .
. 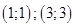
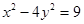 .
. 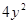 - вправо; тогда
- вправо; тогда 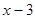 и
и 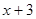 (одной четности) – четные числа, отличающиеся на 6, то есть одно из них делится не только на 2, но и на 4. Следовательно,
(одной четности) – четные числа, отличающиеся на 6, то есть одно из них делится не только на 2, но и на 4. Следовательно, 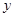 - четное простое число, то есть 2.
- четное простое число, то есть 2. 
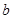 , для каждого из которых существует такое целое число
, для каждого из которых существует такое целое число 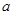 , что дробь
, что дробь 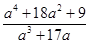 сократима на
сократима на 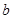 .
. 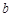 . Поиском занимаемся, либо подгадывая такие комбинации исходных чисел, чтобы степени уменьшались (а в конце получаем число, которое точно делится на
. Поиском занимаемся, либо подгадывая такие комбинации исходных чисел, чтобы степени уменьшались (а в конце получаем число, которое точно делится на 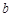 ), либо с использованием деления с остатком ( сродни алгоритму Евклида).
), либо с использованием деления с остатком ( сродни алгоритму Евклида). 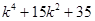 и
и 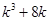 .
. 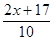 , равно
, равно 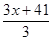 . Найдите все такие действительные значения
. Найдите все такие действительные значения 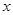 .
. 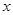 . Решаем. Далее замечаем, что
. Решаем. Далее замечаем, что 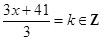 ; выражаем
; выражаем 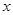 через
через 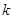 , подставляем в полученное решение неравенства. Выбираем наибольшее целое
, подставляем в полученное решение неравенства. Выбираем наибольшее целое 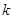 . Находим
. Находим 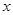 , пишем в ответ.
, пишем в ответ. 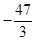
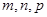 , для которых верно равенство
, для которых верно равенство 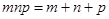 .
. 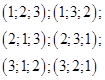
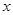 и
и 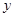 , для которых выполняется равенство
, для которых выполняется равенство 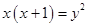 .
. 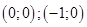
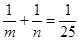 , где
, где 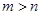 .
. 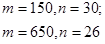
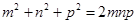 .
. 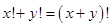 .
. 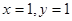
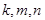 , удовлетворяющие уравнению
, удовлетворяющие уравнению 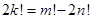 .
. 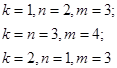
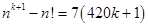 .
. 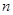 меньше 7 (перебрать легко, тем более если еще что-нибудь отсеять….) и не меньше 7 (здесь поработать с делимостью).
меньше 7 (перебрать легко, тем более если еще что-нибудь отсеять….) и не меньше 7 (здесь поработать с делимостью). 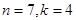
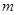 и
и 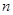 , являющиеся решениями уравнения
, являющиеся решениями уравнения 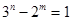 .
. 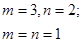
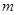 и
и 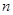 , являющиеся решениями уравнения
, являющиеся решениями уравнения 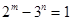 .
. 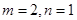
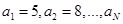 и
и 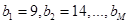 совпадают, а сумма всех совпадающих (взятых по одному разу) членов этих погрессий равна 815. Найдите число членов в каждой прогрессии.
совпадают, а сумма всех совпадающих (взятых по одному разу) членов этих погрессий равна 815. Найдите число членов в каждой прогрессии. 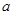 и
и 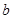 , удовлетворяющие равенству
, удовлетворяющие равенству 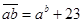 ( в левой части равенства стоит число, получаемое приписыванием десятичной записи числа
( в левой части равенства стоит число, получаемое приписыванием десятичной записи числа 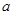 перед десятичной записью числа
перед десятичной записью числа 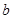 )
) 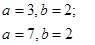
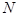 равно произведению 10 различных натуральных чисел, больших 1. Какое наименьшее число различных натуральных делителей (включая единицу и само число) может иметь число
равно произведению 10 различных натуральных чисел, больших 1. Какое наименьшее число различных натуральных делителей (включая единицу и само число) может иметь число 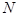 ?
? 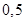 . Оказалось, что сумма каждых пятнадцати из этих шестнадцати чисел положительна. Какое наименьшее целое значение может иметь наименьшее из данных чисел?
. Оказалось, что сумма каждых пятнадцати из этих шестнадцати чисел положительна. Какое наименьшее целое значение может иметь наименьшее из данных чисел? 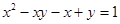
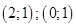
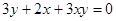 .
. 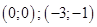
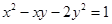 .
. 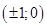
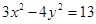 не имеет решений в целых числах.
не имеет решений в целых числах. 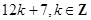
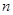 число
число 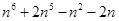 делится на 120?
делится на 120? 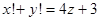 .
. 
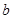 , для каждого из которых существует такое целое число
, для каждого из которых существует такое целое число 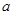 , что дробь
, что дробь 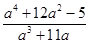 можно сократить на
можно сократить на 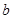 .
. 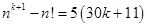 .
. 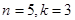
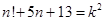 .
. 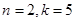
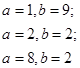

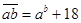 ( в левой части равенства стоит число, получаемое приписыванием десятичной записи числа
( в левой части равенства стоит число, получаемое приписыванием десятичной записи числа 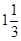 . Оказалось, что сумма каждых семи из этих восьми чисел положительна. Какое наименьшее целое значение может иметь наименьшее из данных чисел?
. Оказалось, что сумма каждых семи из этих восьми чисел положительна. Какое наименьшее целое значение может иметь наименьшее из данных чисел?