Основные числовые характеристики вектора остатков в классической множественной регрессионной модели

Классическая линейная модель множественной регрессии (КЛММР) представляет собой простейшую версию конкретизации требований к общему виду функции регрессии f(X), природе объясняющих переменных X и статистических регрессионных остатков e(Х) в общих уравнениях регрессионной связи. В рамках КЛММР эти требования формулируются следующим образом:

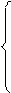Yi=ϴ0+ϴ1xi+…+ϴpxi+εi , i=1,2,…,n

Eεi=0, i=1,2,…,n

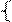E(εiεj)= Ϭ2 при i=j

0 при i не=j (2.5)

(x(1),x(2),…,x(p)) – неслучайные переменные

ранг матрицы X=p+1<n

(матрица X определена соотношением (2.4))

Из (2.5) следует, что в рамках КЛММР рассматриваются только линейные функции регрессии, т.е.

f(X)=E(y|X)= ϴ₀+ϴ₁x⁽¹⁾+…+ϴpx^(p) (2.6)

где объясняющие переменные x⁽¹⁾, x⁽²⁾,…, x^(p) играют роль неслучайных параметров, от которых зависит закон распределения вероятностей результирующей переменной y. Это, в частности, означает, что в повторяющихся выборочных наблюдениях (x_i⁽¹⁾, x_i⁽²⁾,...,х_i^(p);y_i) единственным источником случ возмущений значений y_i являются случайные возмущения регрессионных остатков e_i.

Кроме того, постулируется взаимная некоррелированность случайных регрессионных остатков (E(e_ie_j) = 0 для i ¹ j). Это требование к регрессионным остаткам e₁,...,e_n относится к основным предположениям классической модели и оказывается вполне естественным в широком классе реальных ситуаций, особенно, если речь идет о пространственных выборках (2.4^а)-(2.4^б), т.е. о ситуациях, когда значения анализируемых переменных регистрируются на различных объектах (индивидуумах, семьях, предприятиях, банках, регионах и т. п.). В этом случае данное предположение означает, что «возмущения» (регрессионные остатки), получающиеся при наблюдении одного какого-либо обследуемого объекта, не влияют на «возмущения», характеризующие наблюдения над другими объектами, и наоборот.

Тот факт, что для всех остатков e₁,e₂,...,e_n выполняется соотношение Ee_i²; =s² , где величина s² от номера наблюдения i не зависит, означает неизменность (постоянство, независимость от того, при каких значениях объясняющих переменных производятся наблюдения) дисперсий регрессионных остатков. Последнее свойство принято называть гомоскедастичностью регрессионных остатков.

33. Отражение в модели влияния неучтённых факторов и времени.

Начнем с рассмотрения простейшей модели: Y=α+β_x+u

Величина у, рассматриваемая как зависимая переменная, состоит из двух составляющих:

1) неслучайной составляющей α+β_x, где х выступает как объясняющая (или независимая) переменная, а постоянные величины α и β — как параметры уравнения; 2) случайного члена и.

Почему же существует случайный член?

Одной из причин является невключение объясняющих переменных.

Соотношение между у и х почти наверняка является очень большим упрощением. В действительности существуют другие факторы, влияющие на у, которые не учтены в формуле.

Влияние этих неутенных факторов приводит к тому, что наблюдаемые точки лежат вне прямой.

Часто происходит так, что имеются переменные, которые мы хотели бы включить в регрессионное уравнение, но не можем этого сделать потому, что не знаем, как их измерить, например психологические факторы. Возможно, что существуют также другие факторы, которые мы можем измерить, но которые оказывают такое слабое влияние, что их не стоит учитывать. Кроме того, могут быть факторы, которые являются существенными, но которые мы из-за отсутствия опыта таковыми не считаем. Объединив все эти составляющие, мы получаем то, что обозначено как и. Если бы мы точно знали, какие переменные присутствуют здесь, и имели возможность точно их измерить, то могли бы включить их в уравнение и исключить соответствующий элемент из случайного члена. Проблема состоит в том, что мы никогда не можем быть уверены, что входит в данную совокупность, а что — нет.

Отражение в модели факторов времени

Спецификация моделей Модели временных рядов. Временным рядом называют такую экономическую модель, в которой эндогенная переменная Y t является функцией целочисленного аргумента t .

Спецификация моделей Спецификация моделей временных рядов. y t = T t + S t + u t (2.8) y t = T t ∙ S t + u t (2.9) В моделях (2.8) и (2.9) функция T t отражает влияние факторов, оказывающих «вековые» (лежащие за пределами изучения) влияние на эндогенную переменную. Направление их влияния не изменяется в течении изучаемого отрезка времени. Ее называют временным трендом. Функция S t учитывает влияние факторов, которые оказывают циклическое влияние на эндогенную переменную в изучаемый отрезок времени. U t отражает влияние случайных факторов, которые с большой скоростью меняют направление и интенсивность влияния. Модель (2.8) называют аддитивной, а (2.9) мультипликативной. Аддитивная модель используется в случаях, когда амплитуда циклической составляющей не зависит от времени. В противном случае рекомендуется пользоваться мультипликативной моделью.