Тема. Газовые законы. Изопроцессы. Всякая система может находиться в различных состояниях, отличающихся температурой, давлением, объёмом и т.д

Всякая система может находиться в различных состояниях, отличающихся температурой, давлением, объёмом и т.д.

Величины p, V, T и др. характеризующие состояние системы, называются параметрами состояния.

Если какой-либо из параметров меняется внутри системы от точки к точке, то такое состояние называется неравновесным. Если параметры системы во всех точках одинаковы при неизменных внешних условиях, то такое состояние называется равновесным.

Всякий процесс, т.е. переход системы из одного состояния в другое связанно с нарушением равновесия системы. Однако бесконечно медленный процесс будет состоять из последовательности равновесных состояний. Такой процесс называется равновесным. При достаточно медленном протекании реальные процессы могут приближаться к равновесному. Равновесный процесс является обратимым, т.е. система переходит из состояния 1 в состояние 2 и обратно 2 - 1, проходя через одни и те же промежуточные состояния.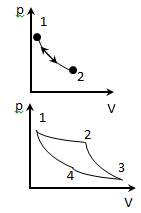

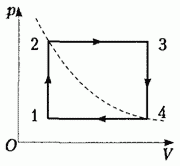
· Процесс, при котором система, пройдя ряд промежуточных состояний, возвращается в исходное состояние, называется круговым процессом или циклом: процесс 1-2-3-4-1 на рисунке.

· Связь между параметрами состояния называется уравнением состояния: f(p,V,T)=0

· Клапейрон, используя законы Бойля-Мариотта и Шарля вывел уравнение состояния идеального газа.

1 – 1’: T = const – закон Бойля – Мариотта: p₁V₁ = p₁’ V₂;

· 1’ – 2: V = const – закон Шарля:

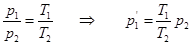
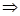
т.к. состояния 1и 2 выбраны произвольно, то для данной массы газа величина остается постоянной

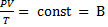· – уравнение Клапейрона

· В- газовая постоянная, различая для различных газов.

· Менделеев объединил уравнение Клапейрона с законом Авогадро

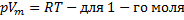( ) V_m- молярный объём

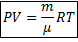
· Уравнение Менделеева-Клапейрона

· R- универсальная (молярная) газовая постоянная.

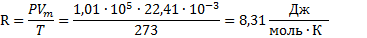
· p = const; ;

·

·

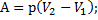
· Физический смысл R: численно равна работе, совершаемой газом при изобарическом (p = const) нагревании одного моля газа ( 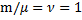) на один Кельвин (?Т=1 К)

· Введем постоянную Больцмана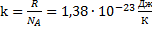

тогда

· =

·

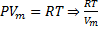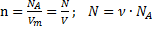
· p = n k T

· p - давление идеального газа при данной температуре прямо пропорционально концентрации его молекул (или плотности газа). При одинаковых p и T все газы содержат в единице объёма одинаковое число молекул.

· n - концентрация молекул (число молекул в единице объёма ). Число молекул, содержащихся при нормальных условиях в 1 м³ называется числом Лошмидта

·

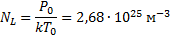
Примеры решения задач:

Задача 1. Вычислить молекулярную массу бензола, зная, что масса 600 мл его паров при 87°C и давлении 83,2 кПа равна 1,30 г.

Решение 1. Выразив данные задачи в единицах СИ и подставив их в уравнение Клапейрона-Менделеева, находим: М = 0,0013*8,31*360/(83200*0,0006) = 0,078 кг/моль = 78 г/моль.

Задача 2. В баллоне объемом V= 10 л находится гелий под давле нием ₁=l МПа при температуре T₁=300 К. После того как из баллона был израсходован гелий массой m=10 г,температура в баллоне понизилась до T₂=290 К. Определить давление ₂ гелия, оставшегося в баллоне.

Решение 2. Для решения задачи воспользуемся уравнением Клапейрона — Менделеева, применив его дважды к начальному и конечному состояниям газа. Для начального состояния уравнение имеет вид

p₁V(m₁/M)RT₁, (1) а для конечного состояния —

p₂V(m₂/M)RT₂, (2) где m₁ и m₂ — массы гелия в начальном и конечном состояниях.

Выразим массы m₁ и m₂ гелия из уравнений (1) и (2):

m₁=Mp₁V/(RT₁); (3)

m₂=Mp₂V/(RT₂); (4)

Вычитая из (3) равенство (4), получим

.

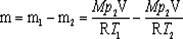Отсюда найдем искомое давление:

.

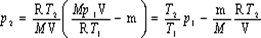Проверим, дает ли правая часть формулы (5) единицу давления. Для этого выразим все величины, входящие в нее, в соответствую­щих единицах. Единица, в которой выражается первое слагаемое, не вызывает сомнений, так как отношение T₂/T₁ — величина без­размерная. Проверим, в каких единицах выражается второе сла­гаемое:

Убедившись в том, что правая часть полученной расчетной фор­мулы дает единицу искомой величины—давления, можем подста­вить в (5) значения всех величин и произвести вычисления.

В формуле (5) все величины, кроме молярной массы М гелия, известны. Найдем ее (см. пример 1). Для гелия как одноатомного газа относительная молекулярная масса равна его относительной атомной массе А_r.

Из таблицы Д. И. Менделеева найдем А_r=4. Следовательно, молярная масса гелия М= А_r10^-3 кг/моль =410^-3 кг/моль. Подставив значения величин в (5), получим

.

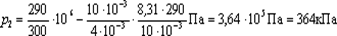Домашнее задание:

1. Учить лекционный материал.

2. Решить задачи:

1. Плотность некоторого газообразного вещества равна 1,5 кг/м³ при 12° C и нормальном атмосферном давлении. Определить молярную массу этого вещества.

2.С идеальным газом, количество вещества которого n = 0,500 моль, совершают замкнутый циклический процесс. Точки 2 и 4 этого процесса находятся на одной изотерме, участки 1 → 2 и 3 → 4являются изохорами, а участки 2 → 3 и 4 → 1 — изобарами. Начертите этот процесс в координатах температуры и объема.

3. Чему равна средняя квадратичная скорость движения молекул идеального газа, если имея массу 6 кг, он занимает объем 5 кубических метров при давлении 200 кПа?

4. В сосуде емкостью 10 л при нормальных условиях находится азот. Определить: число молей азота, массу азота и концентрацию молекул в сосуде.