Расчет дифракционной картины от двух щелей
Имеем физическую ситуацию опыта 2. Положим, что источник электромагнитных волн находится очень далеко от экрана, так что на щели падает плоская электромагнитная волна. Расстояние между щелями 2b, расстояние от экрана со щелями до экрана D, на котором наблюдается дифракционная картина, - L.Пусть ширина щелей гораздо меньше длины волны l, так что вторичные волны, приходящие в точку наблюдения от разных участков щели, имеют практически одинаковые фазы.
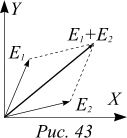Рассчитаем распределение интенсивности электромагнитной волны на экране D как функцию расстояния x от плоскости симметрии до точки наблюдения. Так как напряженность электромагнитной волны в каждой точке представляет собой гармонические колебания, воспользуемся методом векторных диаграмм. Вклад верхней щели в напряженность электрического поля в точке xравен 
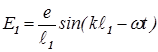.Вклад нижней щели - 
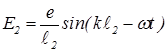.Результирующая напряженность в точке x - E(x)= E1+E2, то есть
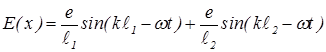. (4)
И первое и второе слагаемые в уравнении (4) равны проекциям на ось ординат векторов с модулям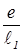и 
и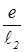 
, вращающимися с одинаковыми угловыми скоростями w. Их сумма равна проекции на ось ординат суммы векторов. Амплитуда колебаний напряженности электрического поля волны Eо(x)равна модулю вращающегося вектора суммы E1+Е2. По теореме косинусов, он равен
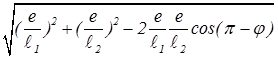, (5)
где j- угол между направлениями складывающихся векторов. Интенсивностьволны I(x) пропорциональна квадрату амплитуды напряженности:
(6)
Угол между направлениями складывающихся векторов jравен разности фаз вкладов: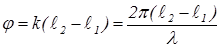 
.При изменении положения приемника x изменяется разность хода l2-l1 и соответственно изменяется, проходя максимумы и минимумы, интенсивность I(x).
Выразим разность фаз через отклонение x. Из чертежа находим
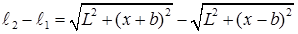(7)
При x, b<<L эта разность приблизительно равна
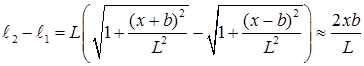(8)
Условие максимума j=2pN (N - целое), что для положений xmaxдает
(9)
Положения минимумов -
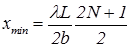. (10)
Формула (6) с подстановкой вычисленной разности фаз j хорошо описывает экспериментальное распределение интенсивности.
Задача 6. На экран с двумя параллельными тонкими щелями, расстояние между которыми равно 4λ, падает пучок монохроматического света. На расстоянии 50 см помещен экран для наблюдения дифракционной картины. Чему равно расстояние между центральным и первым дифракционным максимумом?