ЭЕМ де берілуі және жуықталуы
Абсолюттік және салыстырмалы қателер.
Есептеу кезінде қолданылатын 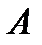 санынан аз ғана айрмашылығы бар
санынан аз ғана айрмашылығы бар 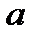 санын жуық сан дейміз. Егер
санын жуық сан дейміз. Егер 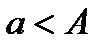 болса,
болса, 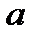 санын кемітіліп алынған, ал
санын кемітіліп алынған, ал 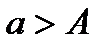 болса, онда артығымен алынған
болса, онда артығымен алынған 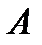 санының мәні дейді.
санының мәні дейді.
Жуықтап алынған а санының қатесі деп 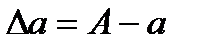 өрнегін айтамыз. Егер
өрнегін айтамыз. Егер 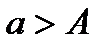 болса, онда
болса, онда 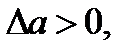 ал
ал 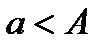 болса, онда
болса, онда 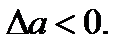 Көп жағдайда
Көп жағдайда 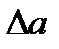 ның таңбасы белгісіз болады. Сондықтан көбінесе
ның таңбасы белгісіз болады. Сондықтан көбінесе 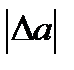 -
-  абсолюттік қате қолданылады. Яғни
абсолюттік қате қолданылады. Яғни
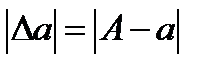 .
.
Егер 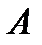 саны бізге белгісіз болса, онда (1.1) формула арқылы абсолюттік қатені анықтау мүмкін емес. Мұндай жағдайда
саны бізге белгісіз болса, онда (1.1) формула арқылы абсолюттік қатені анықтау мүмкін емес. Мұндай жағдайда 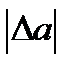 ның жоғарғы шегі-
ның жоғарғы шегі- 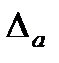 ны анықтайды.
ны анықтайды.
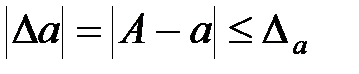 .
.
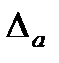 -ны шектік абсолюттік қате деп атайды. (1.2) формуладан мына формуланы аламыз.
-ны шектік абсолюттік қате деп атайды. (1.2) формуладан мына формуланы аламыз.
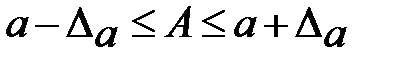
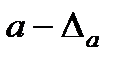 санын
санын 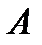 санының кемітілген жуық мәні, ал
санының кемітілген жуық мәні, ал 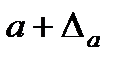 санын арттырылған жуық мәні дейді. Мұндайда
санын арттырылған жуық мәні дейді. Мұндайда 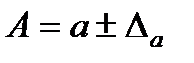 жазуын қолданады.
жазуын қолданады.
Абсолюттік қате, көп жағдайларда есептеу кезінде немесе өлшеу кезінде жіберілген қатені дәл сипаттай алмайды.
Өлшеудің сапасын анықтау үшін салыстырмалы қатені қолданады. Ол былайша табылады:
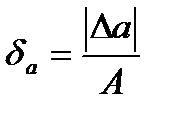 .
.
Ал 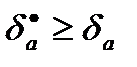 болса, онда
болса, онда 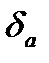 шектік салыстырмалы қате делінеді. Шектік салыстырмалы қате ретінде
шектік салыстырмалы қате делінеді. Шектік салыстырмалы қате ретінде
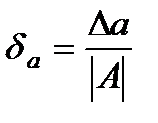
санын алуға болады. Егер 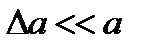 және
және 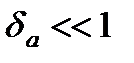 болса, онда абсолюттік қате мен салыстырмалы қатені былайша жуықтап алуға болады:
болса, онда абсолюттік қате мен салыстырмалы қатені былайша жуықтап алуға болады:
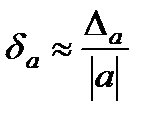
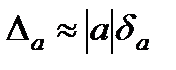
ЭЕМ де берілуі және жуықталуы
#include<iostream.h>
#include<math.h>
void main()
{ double x,y,z, z1,z2;
cout<<"bolwekti engiz->:"<<endl;
cin>>x>>y;
cout<<"tubir astyndagy sandy engiz:"<<endl;
cin>>z;
z1=x/y;
z2=sqrt(z);
cout<<"bolwekten wikkan-> z1="<<z1<<endl;
cout<<"tubirden wikkan-> z2="<<z2<<endl;
cout<<"Juiktaudy esepteimiz->"<<endl;
double f1;
int r;
f1=z1*10000;
r=(int)f1;
if(r%10>=5)
r=r+10;
r=r/10;
f1=(double)r/1000.0;
double f2;
f2=z2*1000;
r=(int)f2;
if(r%10>=5)
r=r+10;
r=r/10;
f2=(double)r/100.0;
double a1,a2,b1,b2;
cout<<"f1="<<f1<<endl;
cout<<"f2="<<f2<<endl;
a1=z1-f1;
a2=z2-f2;
cout<<"Absolutti katelik->"<<endl;
cout<<"a1="<<a1<<endl;
cout<<"a2="<<a2<<endl;
cout<<"Salistirmaly katelik->"<<endl;
b1=a1/f1*100;
b2=a2/f2*100;
cout<<"b1="<<b1<<endl;
cout<<"b2="<<b2<<endl;
if (b1>b2) cout<<"Jauaby:"<<b2<<endl;
else cout<<"Jauap:"<<b1<<endl;}
2. Матрицаның нормасы. Келісілген нормасы. Бағынған нормасы.
Анықтама 1. 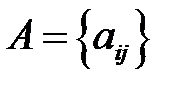 матрицасының нормасы дегеніміз төмендегі шарттарды қанағаттандыратын
матрицасының нормасы дегеніміз төмендегі шарттарды қанағаттандыратын 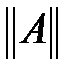 нақты саны:
нақты саны:
а) 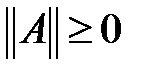
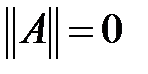

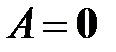 , б)
, б) 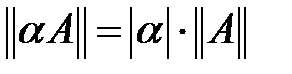 (
( 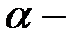 сан),
сан), 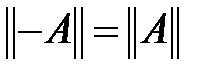 ,
,
в) 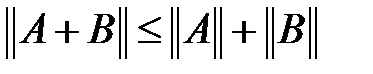 , г)
, г) 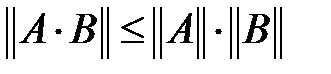 .
.
Квадрат матрицасы үшін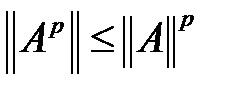
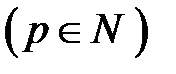 . в) шартын қолданып:
. в) шартын қолданып: 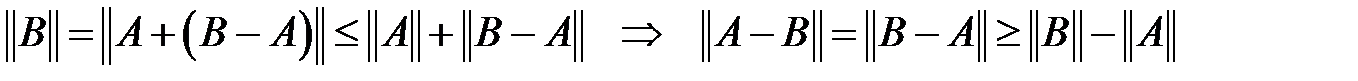 .
.
Соған ұқсас: 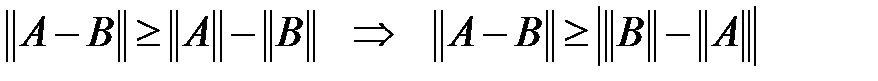 .
.
Анықтама 2. Норма канондық деп аталады, егер қосымша тағы екі шарт орындалса:
д) егер 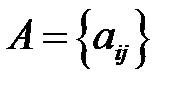 , онда
, онда 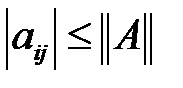 ,
, 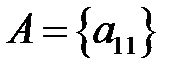 – скаляр матрицасы үшін
– скаляр матрицасы үшін 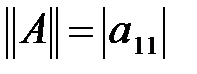 (егер матрица бір ғана саннан тұрса), е)
(егер матрица бір ғана саннан тұрса), е) 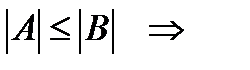 теңсіздігінен
теңсіздігінен 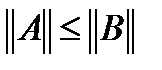 . Дербес жағдайда,
. Дербес жағдайда, 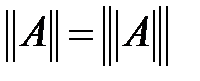 .
.
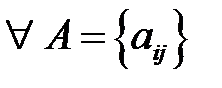 үшін төмендегі нормаларын қарастырамыз:
үшін төмендегі нормаларын қарастырамыз:
1) 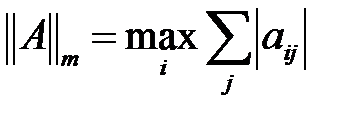 , (
, ( 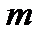 – норма), (I – норма), (тік жол элементтерінің қосындысы).
– норма), (I – норма), (тік жол элементтерінің қосындысы).
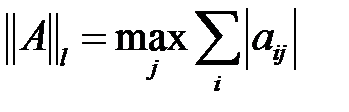 , (
, ( 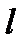 – норма), (II –норма), (жатық жол элементтерінің
– норма), (II –норма), (жатық жол элементтерінің
қосындысы).
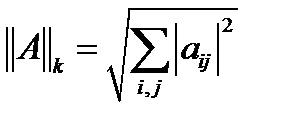 (
( 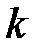 – норма) (III –норма), (Евклид нормасы).
– норма) (III –норма), (Евклид нормасы).
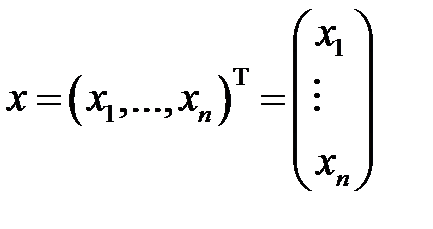 векторы үшін, 1)
векторы үшін, 1) 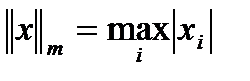 ,
,
2) 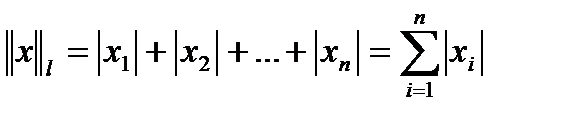 ,
,
3) 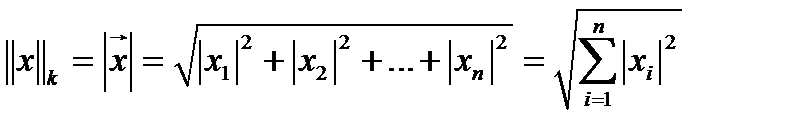 – вектор модулі (ұзындығы).
– вектор модулі (ұзындығы).
Келісілген нормалар
Анықтама 3. 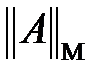 – матрица нормасы
– матрица нормасы 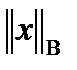 – вектор нормасымен келісілген деп аталады, егер кез–келген
– вектор нормасымен келісілген деп аталады, егер кез–келген 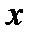 және
және 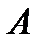 үшін мына теңсіздік орындалса:
үшін мына теңсіздік орындалса: 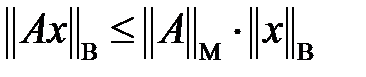 .
.
Анықтама 4. 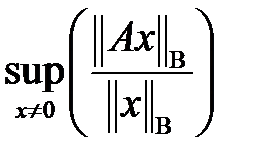 – функционалы
– функционалы 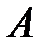 матрицасының нормасы болып табылады және
матрицасының нормасы болып табылады және 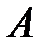 матрицасының
матрицасының 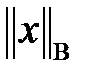 вектор нормасына бағынған нормасы деп аталады.
вектор нормасына бағынған нормасы деп аталады.
Анықтама 5. 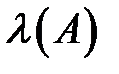 комплекс саны және
комплекс саны және 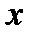 нөлдік емес векторы
нөлдік емес векторы 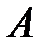 матрицасының сәйкес меншікті саны және меншікті векторы деп аталады, егер
матрицасының сәйкес меншікті саны және меншікті векторы деп аталады, егер 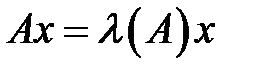 .
.
Анықтама 6. 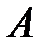 матрицасының барлық меншікті сандарының жиыны
матрицасының барлық меншікті сандарының жиыны 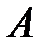 матрицасының спектрі деп аталады.
матрицасының спектрі деп аталады. 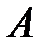 матрицасының
матрицасының 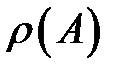 спектралді радиусы деп осы матрицаның меншікті сандары модулдерінің ең үлкенін айтамыз.
спектралді радиусы деп осы матрицаның меншікті сандары модулдерінің ең үлкенін айтамыз.
