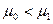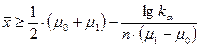Общий подход

Задача проверки гипотезы заключается в определении критической области 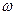максимальной мощности при заданной вероятности ошибки первого рода 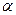. Очевидно, при этом мы будем иметь минимальную вероятность ошибки второго рода .

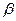При проверке простой гипотезы 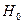против простой альтернативы 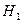эта задача сводится к выбору критической области 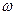, максимизирующей выражение (3.4.), которое в интегральной записи имеет вид

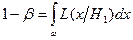, (3.4)

где 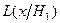- функция правдоподобия при гипотезе 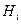(i=0, 1).

При решении задачи требуется, чтобы область 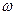удовлетворяла условию

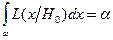(3.5)

Очевидно, выражение (3.5) можно записать так:

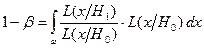
Таким образом, надо выбрать 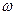так, чтобы максимизировать математическое, ожидание отношения 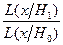, вычисленное в предположении, что справедлива гипотеза 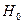. Очевидно, это будет выполнено тогда, когда 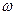, удовлетворяя условию (3.5), содержит точки, для которых отношение 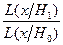принимает наибольшее значение. Следовательно, критическая область 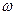состоит из тех точек пространства 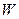, для которых

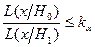. (3.6)

Пример.

Пусть проверяется гипотеза 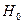: 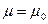против альтернативы 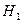: 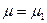, где 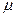- среднее значение нормального распределения .

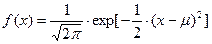Для данного случая

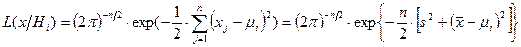, i=0, 1,

где 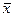, 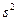- выборочное среднее и дисперсия.

Следовательно соотношение (3.6) можно представить в виде

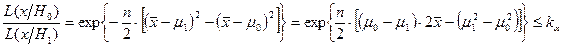
Отсюда

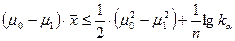
Таким образом, при задани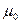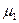и , и 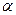наилучшая критическая область определяется только значением выборочного среднего 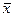. Причем если 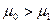, то наилучшая критическая область имеет вид

,

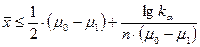если