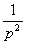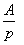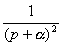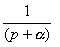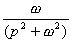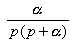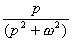Анализ прохождения сложного сигнала через линейную цепь

Часть 2.

Данная часть работы посвящена исследованию искажений сигнала при прохождении его через линейную цепь первого (А) и второго (Б) порядков.

Для каждого студента предлагается свой вариант задания, причем варианты отличаются видом цепочки первого порядка и численными значениями параметров элементов.

Задание на вторую часть курсовой работы (ДЗ2)

А. Определение временной функции напряжения на выходе заданной цепочки первого порядка.

1. Для заданной цепи определить и построить графики частотной, переходной и импульсной характеристик.

2. Построить графики временных функций входного и выходного сигналов при подаче на вход цепочки заданного в ДЗ1 входного сигнала, считая его непериодическим:

а) с помощью интеграла наложения;
б) с помощью операторного метода;
в) частотным методом.

Б. Частотным методом построить выходную функцию напряжения на параллельном колебательном контуре, если заданы его резонансная частота, катушка индуктивности и сопротивление потерь катушки, при подаче на него периодической последовательности импульсов тока, по форме совпадающих с входным сигналом в ДЗ1 (заменить вольты или милливольты на миллиамперы, если в ДЗ1 задано входное напряжение).

1. Определить добротность и полосу пропускания контура.

2. Построить графики АЧХ и ФЧХ контура.

3. Совместить график АЧХ контура и АЧС входного тока, воспользовавшись данными, полученными в ДЗ1.

4. Провести синтез выходного сигнала. Объяснить полученный результат.

Варианты ДЗ2:

Вариант	А. Цепь первого порядка	А. Параметры Цепи 1 порядка	Б. Параметры цепи 2 порядка
R, Ом	L, мкГн	C, мкФ	fp, кГц	L, мкГн	r, Ом
1. Адам
Булекова
3. Гречко		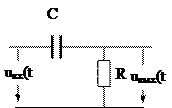		0.001
4. Дубовой		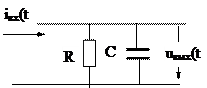		0.02
Жижин		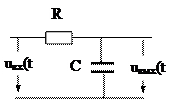		0.02
Карташов
Кудрявцев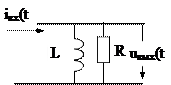
Молодкин
Ураков		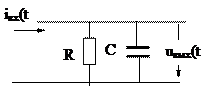		0.035
Юнга
Фурсов				0.01
Белкин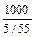
Цыганов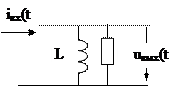
Паршин		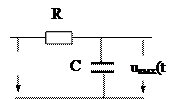		0.011

Методические указания для выполнения данной работы.

А. Цепь первого порядка.

В первом пункте определяются системные передаточные характеристики цепочки, а именно: импульсная, переходная и частотная характеристики. Импульсной передаточной характеристикой называется реакция цепи на воздействие в виде 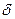-импульса. Переходной характеристикой называется реакция цепи на единичное ступенчатое воздействие. Частотной характеристикой называют комплексный коэффициент передачи цепи при гармоническом воздействии на входе. Самым простым способом определения этих характеристик является использование преобразования Лапласа (операторный метод). В этом методе элементы цепи заменяются их операторными сопротивлениями для сигнала вида 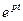: операторное сопротивление активного резистора при этом равно его сопротивлению R, операторное сопротивление индуктивности равно Lр, а операторное сопротивление емкости равно 1/рС. В соответствии с законами Ома и Кирхгофа находится операторная передаточная характеристика, как

.

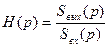Для любых цепей первого порядка , заданных во все вариантах, операторная передаточная функция может быть представлена либо в виде

,

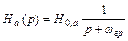либо в виде

.

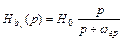Частотная передаточная характеристика определяется заменой в ) :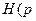

, .

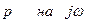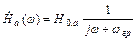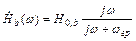Импульсная характеристика цепи является обратным преобразованием Лапласа от операторной передаточной характеристики: 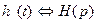. Импульсная характеристика 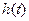называется «оригиналом», для которой имеется «изображение по Лапласу» в виде 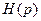. Проще всего производить вычисление обратного преобразования Лапласа (или нахождение оригинала по изображению) по таблице «оригинал-изображение». Ниже дана таблица для часто используемых функций.

Оригинал (t>0) Изображение Оригинал (t>0) Изображение d (t) t A te- a t e- a t sin w t 1- e- a t cos w t

Импульсная характеристика для цепей типа а) находится сразу из таблицы, а именно

.

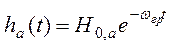Для определения импульсной характеристики цепочки типа б) следует представить операторную передаточную характеристику в виде суммы табличных дробей, например, так:

.

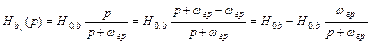Отсюда

.

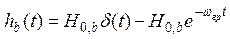Переходная характеристика 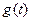также легко может быть определена через операторную передаточную характеристику, поскольку переходная характеристика определяется интегралом от импульсной ( 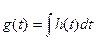.). Изображение и оригинал переходной характеристики определяются как

.

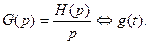Подставив значения параметров цепи, можно построить графики всех системных характеристик.

Далее необходимо определить и построить графики напряжения на выходе цепи.

При использовании метода наложения применяют две записи интеграла Дюамеля.:

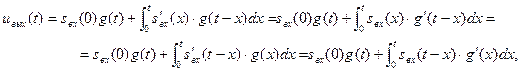(1)

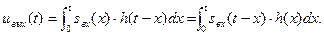(2)

Применяя ту или иную запись интеграла наложения, следует иметь в виду, что производная скачка входного сигнала имеет вид 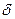-функции, при этом аналитическое вычисление интеграла с 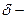функцией несложно, следует лишь помнить избирательное свойство 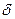-функции, а именно:

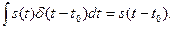
Однако рассчитывать интегралы (1),(2) для сигналов или системных функций с 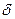-функцией в Маткаде следует с осторожностью, лучше заранее представить подынтегральные функции со скачками в виде суммы ступенчатых функций и функциями без скачков. Кроме того, если импульсная характеристика на заданном элементе схемы имеет в себе дельта-функцию, можно определить сначала ток или напряжение на другом элементе, который описывется импульсной характеристикой без дельта-функции, а затем вычислить уже выходной сигнал с помощью уравнений Кирхгофа.

При использовании операторного метода надо сначала найти изображение по Лапласу заданного входного сигнала 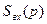, применяя прямое интегрирование по Лапласу, либо используя таблицу оригинал – изображение.

Далее определяется операторное изображение выходного сигнала как произведение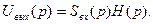

Для определения временной функции выходного напряжения следует представить его операторное изображение в виде суммы простых дробей, для которых в таблице можно найти оригиналы. Тогда само выходное напряжение определится как сумма оригиналов.

Частотный метод нахождения сигнала на выходе линейной цепи требует знания как частотной передаточной характеристики цепи 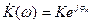, так и частотной характеристики входного сигнала 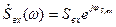. Поскольку заданием предусматривается непериодический входной сигнал, по форме совпадающий с периодическим сигналом, рассмотренным в ДЗ1, то частотная характеристика непериодического сигнала может быть определена как произведение комплексной огибающей на период:

,
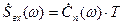где 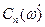- комплексная огибающая спектра периодического сигнала, найденная в ДЗ1, Т – период.

Спектральная плотность выходного напряжения определится как произведение

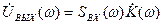или .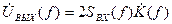

Сама же временная функция определяется интегралом обратного преобразования Фурье

.

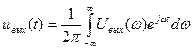В данной работе не предусматривается точное вычисление последнего интеграла. Достаточно лишь рассмотреть качественные искажения сигнала на выходе цепочки. Для качественной оценки формы выходного сигнала следует совместить графики АЧХ сигнала и цепи и сделать вывод об искажениях сигнала, обусловленных частотной характеристики в той или иной области частот и к чему это приведет во временной плоскости. Так, подавление низкочастотной части АЧХ входного сигнала приводит к искажению медленно меняющихся участков его временной функции, а подавление высокочастотных составляющих приводит к уменьшению скорости изменения быстроменяющихся участков.

Б.Цепь второго порядка (параллельный колебательный контур).

. Для использования частотного метода следует определить и построить график АЧХ и ФЧХ колебательного контура. Схема предлагаемого в задании контура имеет вид

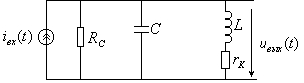
Здесь 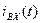- идеальный источник тока.

Частотный коэффициент передачи такого контура имеет вид:

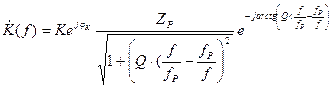
где Q – добротность контура, f_P - резонансная частота, Z_p – резонансное сопротивление контура, причем

.

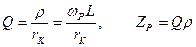Полоса пропускания контура на уровне 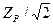определяется отношением

.

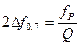Рассчитав основные параметры контура, можно построить его АЧХ и ФЧХ.

Для построения временной функции напряжения на контуре следует сопоставить АЧС входного тока (взять из ДЗ1) и АЧХ контура. Построить график произведения АЧС входного сигнала на АЧХ контура 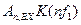. Получим АЧС выходного сигнала. Построить график АЧС выходного напряжения. Сначала провести качественный анализ и записать выводы этого качественного анализа. Затем провести на ЭВМ синтез выходного напряжения по формуле

,

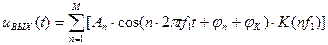выбрав величину М из расчета Мf₁>>f_P.

Построить графики входного и выходного сигналов для сравнительного анализа.