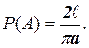Геометрические вероятности

Пусть отрезок 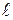составляет часть отрезка 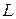. На отрезке 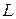наугад поставлена точка. Предполагается , что вероятность попадания точки на отрезок 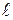пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка 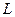. В этих предположениях вероятность попадания точки на отрезок 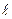определяется равенством

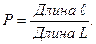
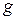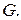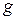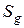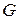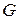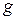Пусть плоская фигура составляет часть плоской фигуры На фигуру наудачу брошена точка. Предполагается, что вероятность попадания брошенной точки на фигуру пропорциональна площади этой фигуры и не зависит от ее расположения относительно фигуры , ни от формы фигуры и . В этих предположениях вероятность попадания точки на фигуру 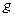определяется равенством

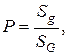где 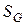- площадь фигуры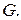

Аналогично определяется вероятность попадания точки в пространственную фигуру 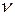, которая составляет часть фигуры .

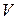Задача № 1.

На отрезок 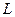, имеющий длину 40 см, помещен меньший отрезок 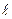длиной 15 см. Найти вероятность того, что точка наудачу поставленная на большой отрезок, попадет также и на меньший отрезок. Предполагается, что вероятность попадания точки на отрезок 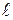пропорциональна длине этого отрезка и не зависит от его расположения на отрезке .

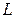Ответ: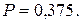

Задача № 2.

Плоскость разграфлена параллельными прямыми, находящимися друг от друга на расстоянии 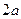. На плоскость наудачу брошена монета радиуса 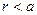. Найти вероятность того, что монета не пересечет ни одной из прямых.

Задача № 3.

Внутрь круга радиуса 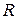наудачу брошена точка. Найти вероятность того, что точка окажется внутри вписанного в этот круг правильного треугольника. Предполагается, вероятность попадания точки в треугольник пропорциональна площади треугольника и не зависит от его расположения относительно круга.

Ответ: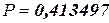

Задача образец.

Два товарища условились встретиться в определенном месте между 12 часами и половиной первого дня. Пришедший первым ждет другого в течении 20 минут, после чего уходит. Найти вероятность того, что встреча товарищей состоится, если каждый из них наудачу выбирает момент своего прихода ( в промежутке от 12 часов до половины первого) и моменты прихода обоих независимы.

Решение.

Обозначим событие: - встреча товарищей состоится.

Найдем вероятность события применив формулу: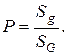

Обозначим момент прихода одного из них через 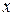мин., а момент прихода другого через 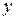мин. Для того, чтобы встреча произошла необходимо и достаточно, чтобы выполнялось условие: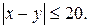

Будем изображать 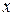и 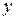как декартовы координаты точек плоскости; в качестве единицы масштаба выберем минуту рис. 1.

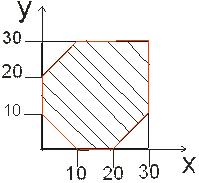
Рис. 1.

Все возможные исходы испытания изображаются точками фигуры ограниченной квадратом, сторона которого равна 30; площадь этого квадрата равна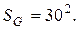

Неравенство 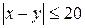равносильно системе неравенств:

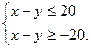
Исходы испытания, благоприятствующие событию , удовлетворяют системе неравенств:

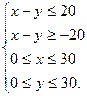
Решениями этой системы неравенств являются координаты всех точек плоскости, расположенных на рис.1 в заштрихованной области, то есть между граничными прямыми: 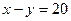; ; 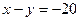; ; 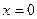; 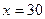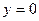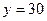и на самих граничных прямых. Точки плоскости, принадлежащие заштрихованной области, характеризуют исходы испытания, благоприятствующие событию . Площадь заштрихованной фигуры равна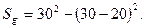

Искомая вероятность события равна отношению площади заштрихованной фигуры к площади всего квадрата:

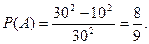
Задача № 4.

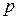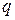Коэффициенты и квадратного уравнения 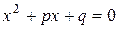выбирают наудачу на отрезке 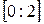. Какова вероятность того, что корни этого уравнения будут действительными числами?

Ответ: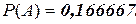

Задача № 5.

Наудачу взяты два неотрицательных числа 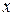и 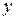, каждое из которых не больше единицы. Найти вероятность того, что сумма 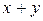не превышает единицы, а их произведение не больше двух .

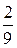Ответ: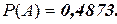

Задача № 6.

Плоскость разграфлена параллельными прямыми, находящимися друг от друга на расстоянии 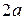. На плоскость наудачу бросают иглу длины 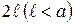. Найти вероятность того, что игла пересечет какую-нибудь прямую.

Ответ: