Область определения. Область значения
Особенности изучения функций в старших классах
§2 Периодичность функций
График функции
Литература:
1. «Алгебра, 11 класс (12-летняя школа)» авторов Е.П.Кузнецовой, Г.Л.Муравьёвой, Л.Б.Шнепермана, Б.Ю.Ящина / под редакцией профессора Л.Б.Шнепермана (Минск: Народная асвета, 2007, 2008) (10 класс)
2. «Математика, 11 класс (12-летняя школа)» авторов Л.А.Латотина, Б.Д.Чеботаревского (Минск: Народная асвета, 2007, 2008) (10 класс)
3. «Алгебра, 11 класс (11-летняя школа)» авторов Е.П.Кузнецовой, Г.Л.Муравьёвой, Л.Б.Шнепермана, Б.Ю.Ящина / под редакцией профессора Л.Б. Шнепермана (Минск: Народная асвета, 2008)(11 класс)
4. «Математика, 11 класс (11-летняя школа)» авторов Л.А.Латотина, Б.Д.Чеботаревского (Минск: Народная асвета, 2008)(11 класс)
5. Азаров А.И.Функции, их свойства и графики. Теория, тесты, задачи. _ Мн.:УниверсалПресс, 2004.
6. Рогановский, Н.М. Методика преподавания математики в средней школе: в 2 частях(часть2). -Могилев, 2011
При подготовке лекции использовались материалы лекций по МПА проф. Ананченко К.О.
Особенности изучения функций в старших классах
В курсе «Алгебра и начала анализа» изучается понятие производной, поэтому многие вопросы, связанные с изучением свойств функций, решаются уже с помощью производной.
В старших классах изучаются новые функции: тригонометрические, степенная, показательная, логарифмическая.
Определим содержание темы, а также знания и умения, которыми должны обладать учащиеся после изучения темы, согласно программе «Математика: V-XI классы, 2009».
1.1 Содержание:
Класс
Четность и нечетность функции. Периодичность функции. Максимумы и минимумы функции.
Производная. Механический и геометрический смысл производной.
Производные элементарных функций.
Правила нахождения производных.
Связи между знаком производной функции и ее возрастанием или убыванием.
Применение производной к исследованию функций.
Уравнение касательной к графику функций.
Нахождение наибольшего и наименьшего значения функции на промежутке.
Функции y=sin x, y=cos x, 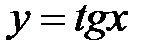 , их свойства и графики.
, их свойства и графики.
Класс
Степенная функция с действительным показателем. Примеры исследования степенных функций с различными рациональными показателями.
Показательная функция. Примеры исследования показательных функций с различными основаниями.
Логарифмическая функция. Примеры исследования логарифмических функций с различными основаниями.
1.2 Знания и умения:
1. Знать термины и правильно использовать понятия:
· максимум функции;
· наибольшее значение функции на промежутке;
· наименьшее значение функции на промежутке;
· четная функция;
· нечетная функция;
· периодическая функция;
· период функции;
· производная функции.
2. Знать особенности графиков четной функции, нечетной функции, периодической функции.
3. Знать определения степенной, показательной, логарифмической и тригонометрических функций.
4. Знать правила нахождения производной суммы, разности, произведения, частного функций.
5. Знать связь между возрастанием (убыванием) функции и знаком ее производной.
6. Уметь решать несложные задачи на нахождение наибольшего и наименьшего значений функций на промежутке.
7. Уметь исследовать функцию с использованием производной.
Основные понятия
Определение предлагается аналогичное изученному в 7 классе:
Определение:Функцией, заданной на множестве D, называется закон, по которому каждому значению х из Dставится в соответствие одно определенное значениеу. [1,с.5]
Область определения. Область значения.
Нахождение областей определения и значений функции очень важно для исследования функций и построения графиков. С помощью заданий можно практически систематизировать знания о свойствах ряда элементарных функций, о методах решении неравенств и систем.
Интересны творческие задания на понимание понятий области определения и множества значений функции:
1) Привести пример функции, заданной аналитически, у которой:
а) область определения есть множество, состоящее из
· одного числа
· двух чисел
· трех чисел
б) множество значений есть множество, состоящее из
· всех чисел, принадлежащих объединению интервалов (- 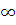 ;-1]
;-1] 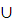 [1;+
[1;+ 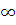 )
)
· всех целых чисел
2) Найти область определения функции
