Б.4 Вычисление характеристик погрешности результата измерений

Б.4.1 Делают предположение о равномерном распределении неисключенных систематических составляющих погрешности результата измерений внутри их границ q_V и q_R. Тогда СКО суммарной неисключенной систематической составляющей погрешности результата измерений силы тока S_q, А, определяют по формуле

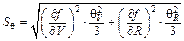, (Б.9)

где 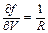, 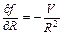- коэффициенты влияния.

Таким образом, получают

,

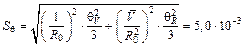= 0,050 %.

Б.4.2 Доверительные границы суммарной неисключенной систематической составляющей погрешности результата измерений силы тока q(p) при доверительной вероятности p = 0,95 оценивают по формуле

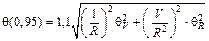= 9,5×10^-3А, (Б.10)

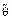(0,95) = 0,095 %.

Б.4.3 СКО случайной составляющей погрешности результата измерений силы тока S определяют по формуле

S = 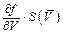= 3,4×10^-3 А, (Б.11)

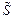= 0,034 %.

Б.4.4 СКО суммарной погрешности результата измерений силы тока S_S вычисляют по формуле

S_S = 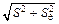= 6,0×10^-3 А, (Б.12)

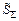= 0,060 %.

Б.4.5 Доверительные границы погрешности результата измерений силы тока D_0,95 при p = 0,95 и эффективном числе степеней свободы f_эф = n – 1 = 9 вычисляют по формуле

D_0,95 = 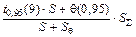= 0,012 A, (Б.13)

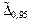= 0,12 %.

Б.5 Вычисление неопределенности измерений

Б.5.1 По типу А вычисляют стандартную неопределенность, обусловленную источниками неопределенности, имеющими случайный характер.

Б.5.1.1 Стандартную неопределенность напряжения, обусловленную источниками неопределенности, имеющими случайный характер, u_A(V) определяют по формуле

u_A(V) = 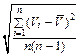, (Б.14)

u_A(V) = 3,4×10^-2 мВ,

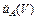= 0,034 %.

Б.5.1.2 Стандартную неопределенность силы тока, обусловленную источниками неопределенности, имеющими случайный характер, u_A определяют по формуле

u_A = 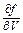× u_A(V) = 3,4×10^-3 А, (Б.15)

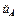= 0,034 %.

Б.5.2 По типу В вычисляют стандартные неопределенности, обусловленные источниками неопределенности, имеющими систематический характер. Распределение значений величин внутри границ считают равномерным.

Б.5.2.1 Границы систематического смещения при измерениях напряжения, определенные при калибровке вольтметра, равны 3×10^-4×V + 0,02. Тогда соответствующую стандартную неопределенность u_B,V вычисляют по формуле

u_B,V = 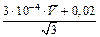= 2,9×10^-2 мВ, (Б.16)

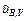= 0,029 %.

Б.5.2.2 Границы, внутри которых лежит значение сопротивления шунта, определены при калибровке шунта и равны 7×10^-4R. Тогда при R = R₀ соответствующую стандартную неопределенность u_B,R вычисляют по формуле

u_B,R = 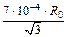= 4,0×10^-6 Ом, (Б.17)

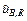= 0,040 %.

Б.5.2.3 Границы изменения значения сопротивления шунта, обусловленного изменением температуры, равны a×Dt×R₀. Соответствующую стандартную неопределенность u_B,t получают в соответствии с формулой

u_B,t = 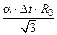= 1,7×10^-9 Ом, (Б.18)

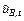= 1,7×10^-5 %.

В дальнейшем этой составляющей неопределенности (ввиду ее малости по сравнению с другими составляющими) можно пренебречь.

Б.5.2.4 Суммарную стандартную неопределенность u_B, вычисленную по типу В, определяют по формуле

u_B = 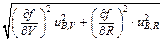= 5,0×10^{-3 A, (}Б.19)

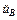= 0,050 %.

Б.5.3 Суммарную стандартную неопределенность u_c вычисляют по формуле

u_c = 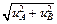= 6,0×10^-3 А, (Б.20)

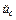= 0,060 %.

Б.5.4 Эффективное число степеней свободы v_eff рассчитывают по формуле

v_eff = 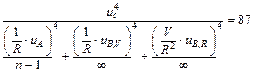. (Б.21)

Б.5.5 Коэффициент охвата k получают по формуле

k = t_0,95(v_eff) = 1,99. (Б.22)

Б.5.6 Расширенную неопределенность U_0,95 определяют следующим образом

U_0,95 = k×u_c = 0,012 А, (Б.23)

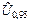= 0,12 %