Теңдеулерді шешудің Лагранж əдісі
Сызықтық біртекті емес дифференциалдық теңдеудің жалпы шешімін табу үшін практикада Лагранж әдісі (тұрақтыны вариациялау әдісі) қолдану ыңғайлы.
Алдымен берілген теңдеуге сәйкес біртекті теңдеудің жалпы шешімін табу керек. Алдында қарастырылғандай ол мына түрде жазылады:
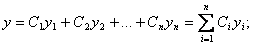
Содан соң, Ci коэффициенттерін х-тің функциялары деп есептеп, біртекті емес теңдеудің дербес шешімін табу керек:
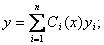
Ci(x) функцияларын табу үшін келесі жүйені шешу керек:

Мысалы: 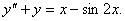 теңдеуін шешу керек.
теңдеуін шешу керек.
Шешуі: 1) Әуелі 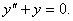 біртекті теңдеуді шешеміз.
біртекті теңдеуді шешеміз.
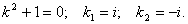
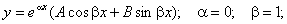
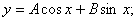
2) Біртекті емес теңдеудің шешімі келесі түрде болады:
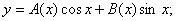
Теңдеулер жүйесін құрастырамыз:
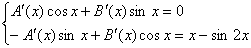
Жүйені шешейік:
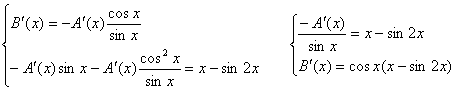
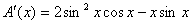 өрнегінен А(х) функциясын табамыз.
өрнегінен А(х) функциясын табамыз.
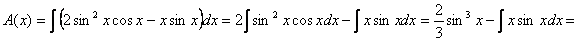

Енді В(х) функциясын табайық.
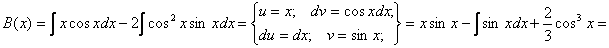
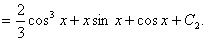
Табылған мәндерді біртекті емес теңдеудің шешімінің формуласына қоямыз:
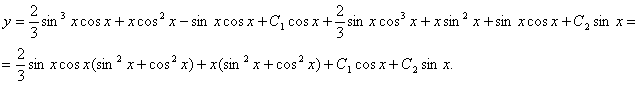
Жауабы: 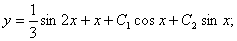
Сөйтіп, біртекті емес теңдеудің жалпы шешімін дара шешімін таппастан жаздық.
Аудиториялық жұмыстар
Берілген теңдеулердің жалпы шешімін тап.
1) y"'-4y"+5y'-2y=2x+3 Жауабы: y=(c1+c2x)ex+c3e2x-x-4.
2) y"'-3y'+2y=e-x(4x2+4x-10) Жауабы: y=(c1+c2x)ex+c3e-2x+(x2+x-1)e-x
3) yIV+8y"+16y=cos x Жауабы:y=(c1+c2x)cos2x+(c3+c4x)sin2x+1/9cos x
4) yIV+2α 2y "+α 4y=cos αx Жауабы: y=(c1+c2x)cosαx+(c3+c4x)sinαx-x2cos αx/ 8α2
5) yV+y"'=x2 –1 Жауабы: y=1/60x5–1/2 x3+c1 x2+c2 x+c3+c4cos x+c5sin x
6) yIV-y=xex + cos x Жауабы: y=c1ex+c2e-x+c3sinx+c4cos x+x2-3x/8*ex-1/4 xsin x
Й жұмыстары
Берілген теңдеулердің жалпы шешімін тап.
7) yIV-2y"+y=8(ex + e-x)+4(sinx+cosx) Жауабы: y=(c1 +c2 x+x2)ex +(c3+c4x+x2)e-x+ +sin x +cos x
8) y"'+2y"+y'+2e-2x =0; y|x=0=2, y'|x=0=1,y"|x=0=1 Жауабы: y=4-3e-x +e-2x
9) y"'-y'=3(2-x); y|x=0=y'|x=0=y"|x=0=1 Жауабы: y=ex +x3
10) Эйлер теңдеуін шеш: x3y"'+xy'-y=0 Жауабы: y=x(c1+c2ln|x| +c3ln2|x|)
ЖӘЙ Дифференциалдық теңдеулер жүйесі
Жәй дифференциалдық теңдеулер жүйелері. Жүйенің нормальдық қалпы.
Анықтама. Төменде берілген теңдеулер жүйесі:
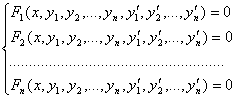
бірінші ретті дифференциалдық теңдеулержүйесі деп аталады, мұндағы х-тәуелсіз айнымалы, у1, у2,…,уn – ізделінді функциялар.
Ал, егер жүйе ізделінді функциялардың туындылары арқылы шешілген болса, яғни :
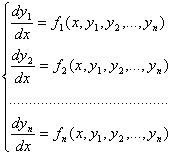
онда нормальдық жүйе деп аталады.
Теорема. (Коши теоремасы). Егер (n-1) –өлшемді кеңістіктің қандайда бір аймағында нормальдық жүйенің оң жағындағы
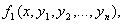
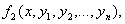 …
… 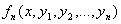
функциялары үзіліссіз және 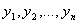 бойынша дербес туындылары бар болса, онда осы аймақтың кез-келген
бойынша дербес туындылары бар болса, онда осы аймақтың кез-келген 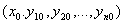 нүктелері үшін
нүктелері үшін 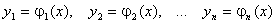 бастапқы шарттарын қанағаттандыратын, жүйенің жалғыз шешімі бар болатын аймақ табылады.
бастапқы шарттарын қанағаттандыратын, жүйенің жалғыз шешімі бар болатын аймақ табылады.
Коши теоремасының шарттары орындалатын аймақта, жүйенің жалпы шешімі болатын функциялар жиынтығынан Кошидың кез келген есебінің шешімін алуға болады.
Анықтама. Дифференциалдық теңдеулер жүйесінің жалпы шешімі деп теңдеулер жүйесін теңбе-теңдікке айналдыратын
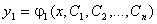 ,
, 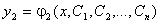 , …
, … 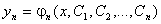
функциялар жиынтығын айтады.
4.2 Тұрақты коэффициентті сызықтық дифференциалдық
