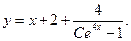Уравнения, приводимые к линейным
Тема 5. Линейные уравнения первого порядка и
Уравнения, приводящиеся к ним
Линейные уравнения первого порядка
Уравнение 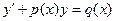 (5.1) линейное относительно неизвестной функции
(5.1) линейное относительно неизвестной функции 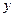 , (а также любое уравнение, с помощью алгебраических преобразований приводящиеся к виду (5.1)), называется неоднородным линейным дифференциальным уравнением первого порядка.
, (а также любое уравнение, с помощью алгебраических преобразований приводящиеся к виду (5.1)), называется неоднородным линейным дифференциальным уравнением первого порядка.
Функция 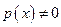 ,
, 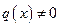 должны быть непрерывными в некоторой области, например на отрезке [a;b], для того, чтобы выполнялись условия теоремы Коши существования и единственности решения.
должны быть непрерывными в некоторой области, например на отрезке [a;b], для того, чтобы выполнялись условия теоремы Коши существования и единственности решения.
Если в (5.1) 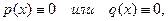 то получим дифференциальные уравнения с разделяющимися переменными.
то получим дифференциальные уравнения с разделяющимися переменными.
В случае, когда 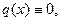 уравнение (5.1) называют однородным линейным дифференциальным уравнением.
уравнение (5.1) называют однородным линейным дифференциальным уравнением.
Общее решение уравнения (5.1) всегда можно записать в виде
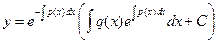 (5.2)
(5.2)
где С – произвольная постоянная.
Наиболее употребительным способом решения уравнения (5.1) является метод вариации произвольной постоянной.Сущность метода состоит в следующем. Сначала ищется решение однородного уравнения, соответствующего уравнению (5.1):
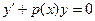 (5.3)
(5.3)
Затем в общем решении уравнения (5.3) произвольную постоянную С считают некоторой дифференцируемой функцией от x: C=C(x). Эту функцию находят из дифференциального уравнения с разделяющимися переменными, которое получается в результате подстановки общего решения уравнения (5.3) в уравнении (5.1).
Пример 5.1. Решить уравнение 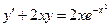 (5.4)
(5.4)
Сначала находим решение однородного уравнения, соответствующего данному: 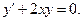 Разделяя переменные и интегрируя, находим:
Разделяя переменные и интегрируя, находим: 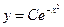 (5.5)
(5.5)
Формула (5.5) представляет собой общее решение однородного уравнения, где С – произвольная постоянная. Для получения всех решений данного уравнения считаем C=C(x) и требуем, чтобы функция 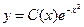 удовлетворяла уравнению (5.4), т.е.
удовлетворяла уравнению (5.4), т.е.
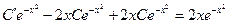 или
или 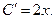 Отсюда находим
Отсюда находим 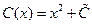 (5.6)
(5.6)
где 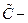 новая произвольная постоянная. Подставив (5.6) в (5.5), окончательно получим
новая произвольная постоянная. Подставив (5.6) в (5.5), окончательно получим 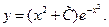
Обмен ролями между функцией и аргументом
Некоторые уравнения становятся линейными, если в них поменять ролями функцию и аргумент.
Пример 5.2. Решить уравнение 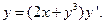
Предложенное уравнение линейное относительно 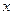 . Так как
. Так как 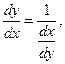 то его можно записать в виде
то его можно записать в виде 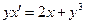 или
или 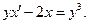 (5.7)
(5.7)
Общим решением однородного уравнения 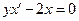 является функция
является функция 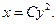 (5.8)
(5.8)
Считая, что 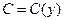 , и подставляя (5.8) в (5.7), получим последовательно
, и подставляя (5.8) в (5.7), получим последовательно
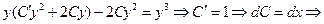
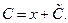 (5.9)
(5.9)
Подставляя (5.9) в (5.8), имеем общее решение 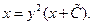
Уравнения, приводимые к линейным
К линейным уравнениям приводятся также уравнения вида:
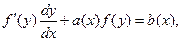 (5.10)
(5.10)
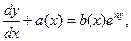 (5.11)
(5.11)
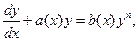 (5.12)
(5.12)
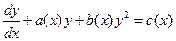 (5.13)
(5.13)
Уравнение вида (5.10) сводится к линейному, если положить 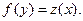 Тогда получаем
Тогда получаем 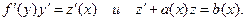
В уравнении (5.11) целесообразно провести замену 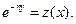 Тогда получим
Тогда получим 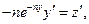
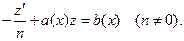
Уравнение (5.12) называется уравнением Бернулли. Оно приводится к линейному с помощью замены 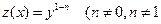 , так как в этих случаях оно уже линейное).
, так как в этих случаях оно уже линейное).
Пример 5.3. Решить уравнение 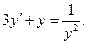
Чтобы свести данное уравнение Бернулли к линейному, разделим обе части на выражение 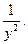 Получаем
Получаем 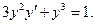 (5.14)
(5.14)
Произведем замену 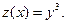 (5.15)
(5.15)
Тогда 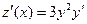 (5.16)
(5.16)
Подставим (5.15) и (5.16) в (5.14), имеем 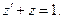
Последнее уравнение не только линейное, но и является уравнением с разделяющимися переменными 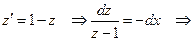
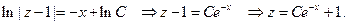 Производя обратную подстановку, получаем общее решение исходного уравнения
Производя обратную подстановку, получаем общее решение исходного уравнения 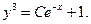
Уравнение (5.13) называется уравнением Риккатти. В общем случае уравнение Риккатти не решается в квадратурах. Если же известно частное решение 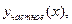 то уравнение (5.13) сводится к уравнению Бернулли с помощью замены
то уравнение (5.13) сводится к уравнению Бернулли с помощью замены 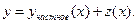 Если частное решение неизвестно, то его ищут по виду правой части (5.13), понижая при этом его степень.
Если частное решение неизвестно, то его ищут по виду правой части (5.13), понижая при этом его степень.
Пример 5.4. Решить уравнение 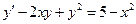 (5.17)
(5.17)
Поскольку правая часть уравнения Риккатти представляет собой квадратичное выражение, то частное решение будем искать в виде 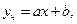 (5.18)
(5.18)
где 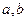 - неизвестные коэффициенты, которые находим, подставляя (5.18) в (5.17), приравнивая коэффициенты при соответствующих степенях
- неизвестные коэффициенты, которые находим, подставляя (5.18) в (5.17), приравнивая коэффициенты при соответствующих степенях 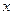 , т.е. получаем последовательно
, т.е. получаем последовательно 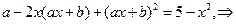
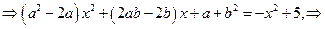
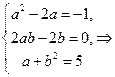
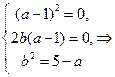
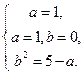
Если b=0, то последнее уравнение системы не будет выполняться, т.к. 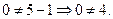
Следовательно, 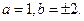 Значит, за частное решение можно принять либо
Значит, за частное решение можно принять либо 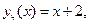 либо
либо 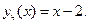
Допустим 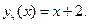 Делаем замену
Делаем замену 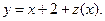 (5.19)
(5.19)
Подставляя (5.19) в (5.17), получим 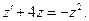
Последнее является уравнением Бернулли. Сводим его к линейному, поделив обе части на 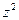 :
: 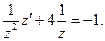 (5.20)
(5.20)
Производим замену 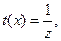 тогда
тогда 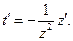 Подставляя замену в (5.20), получаем
Подставляя замену в (5.20), получаем 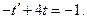 Решая последнее как уравнение с разделяющимися переменными, получаем общее решение уравнения (5.20)
Решая последнее как уравнение с разделяющимися переменными, получаем общее решение уравнения (5.20) 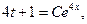 или
или 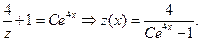 Подставляя последнее выражение в (5.14), получим общее решение исходного уравнения (5.17)
Подставляя последнее выражение в (5.14), получим общее решение исходного уравнения (5.17)