Контрольная расчетная работа по динамике

Задача 3.1

Задача 3.1 относится к прямой задаче динамики точки: по известным (заданным) силам и начальным условиям движения требуется определить движение точки, получив уравнения движения. Для этого следует изобразить движущееся тело (точку) в произвольный момент времени, показать все действующие на тело (заданные) силы, освободиться от связей, заменив их действие соответствующими реакциями. Затем составить дифференциальные уравнения движения (два при криволинейном и одно при прямолинейном движениях) и проинтегрировать их. Значения постоянных интегрирования определить из начальных условий. Исходные данные для различных вариантов даны в табл. 9.

Таблица 9

Цифра шифра	1-я цифра шифра	2-я цифра шифра	3-я цифра шифра
v0, м/с	a, м	b, м	a, град	Силы, Н	Номер условия	Номер схемы (рис. 18)	f
F	P
		4,5	1,0				3.1.1		–
		5,0	1,5				3.1.1		–
		5,5	2,0				3.1.1		–
		6,0	2,5				3.1.1		–
		6,5	3,0				3.1.2		–
		7,0	3,5				3.1.2		–
		7,5	4,0				3.1.3		0,10
		8,0	4,5				3.1.3		0,12
		8,5	5,0				3.1.4		0,14
		9,0	5,5				3.1.4		0,16

Условия

3.1.1. Тяжелая материальная точка М брошена под углом a к горизонту со скоростью v₀. В начальный момент времени точка находилась в положении М₀. Пренебрегая сопротивлением среды, определить уравнения движения точки в заданной системе координат (см. рис. 18, схемы 1 – 4).

3.1.2. Тело М весом Р брошено вертикально вверх (см. рис. 18, схема 5) или вниз (см. рис. 18, схема 6) со скоростью v₀. При движении на тело действует сила ветра F. В начальный момент тело находилось в положении М_о. Определить уравнение движения, приняв его за материальную точку, в заданной системе координат (см. рис. 18, схемы 5, 6).

3.1.3. Груз весом Р движется прямолинейно по горизонтальной плоскости. На груз действует сила F, составляющая с горизонталью угол a. Коэффициент трения скольжения груза о плоскость равен f. В начальный момент времени груз находился в положении М_о на расстоянии a от начала координат и имел скорость v₀. Определить уравнение движения груза в заданной системе координат (см. рис. 18, схемы 7, 8).

3.1.4. Груз весом Р движется вверх (см. рис. 18, схема 9) или вниз (см. рис. 18, схема 10) по шероховатой наклонной плоскости. Коэффициент трения скольжения груза о плоскость равен f. В начальный момент груз находился в положении М_о на расстоянии a от начала координат и имел скорость v₀. Определить уравнение движения груза в заданной системе координат (см. рис. 18, схемы 9, 10).

Примечание. Для схем 8 и 9 определить уравнение движения груза на первом этапе, когда движение происходит в направлении начальной скорости.

Пример решения задачи 3.1

Условие. Груз весом Р движется вниз по шероховатой наклонной плоскости, составляющей угол a=30°с горизонтом. Коэффициент трения скольжения груза о плоскость f=0,16. В начальный момент груз находился в положении М_о на расстоянии a=9 м от начала координат и имел скорость v₀=30 м/с.

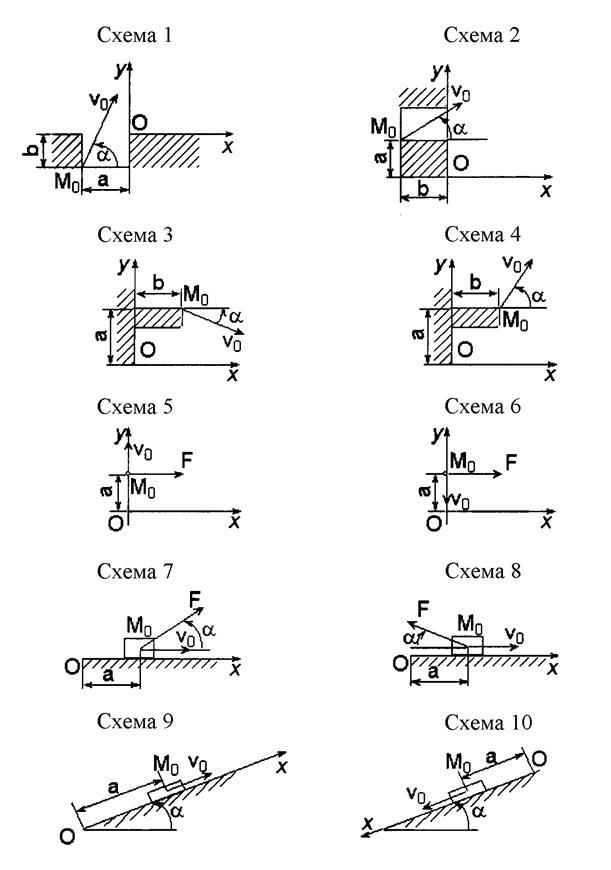
Рис. 18. Схемы к задаче 3.1
Определить уравнение движения груза в заданной системе координат (рис. 19).

Рис. 19

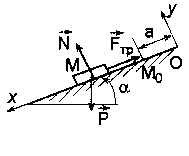
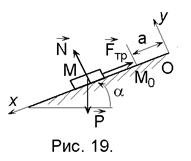Решение. 1. Пусть тело в произвольный момент времени t занимает положение М на наклонной плоскости. Освободим тело от связи (шероховатой наклонной плоскости), заменив ее действие нормальной составляющей реакции N и силой трения F_тр. Тогда тело будет двигаться под действием системы трех сил (Р, N, F_тр).

2. Примем тело за материальную точку. Проектируя основное уравнение динамики точки

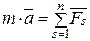
на оси декартовых координат Оx и Оy (ось Оx совпадает с направлением движения точки), получим два дифференциальных уравнения:

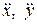Здесь m – масса точки; – проекции ускорения точки на соответствующие оси.

Так как тело движется прямолинейно вдоль оси Оx, то проекция ускорения на ось Оy равна нулю, следовательно, уравнение (2) примет вид .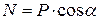

Сила трения по закону Кулона равна 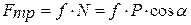. С учетом этого выражения дифференциальное уравнение (1) примет следующий вид:

.

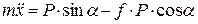После замены 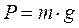, где 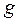– ускорение свободного падения тела, и очевидных преобразований получим следующее дифференциальное уравнение второго порядка:

.

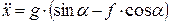Для понижения порядка уравнения произведем замену 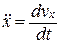, получим дифференциальное уравнение первого порядка с разделяющимися переменными:

.

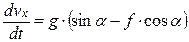Разделив переменные, проинтегрируем дифференциальное уравнение с учетом начальных условий (при t=0, v_x=v₀):

Произведем замену для понижения порядка уравнения 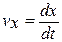и, разделив переменные, проинтегрируем дифференциальное уравнение второй раз с учетом начальных условий (при t=0 x=x₀=a):

Подставив в соотношение (4) значения заданных величин, получим окончательно следующее уравнение движения груза:

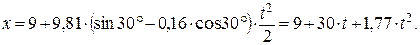
Задача 3.2

Данная задача решается с применением теоремы об изменении кинетической энергии механической системы. Прежде всего требуется определить систему, т.е. перечислить те тела, которые включены в состав системы. Затем нужно изобразить систему в произвольный момент времени, показать все силы (заданные и реакции связей), действующие на тела системы, определить скорости тел и перемещения точек приложения сил. После этого необходимо вычислить кинетическую энергию системы в начальном и конечном положениях, вычислить работу всех сил на заданных перемещениях и подставить полученные результаты в формулу, выражающую теорему об изменении кинетической энергии механической системы в конечной (интегральной) форме. Исходные данные приведены в табл. 10.

Таблица 10

Цифра шифра	1-я цифра шифра	2-я цифра шифра	3-я цифра шифра
r, см	S, м	M, Н м	Силы, кН	Номер схемы (рис. 20)	a, град	f
P	Q	F
		2,1		1,1	3,1	8,1+0,5S			0,06
		2,2		1,2	3,2	8,2+0,4S			0,07
		2,3		1,3	3,3	8,3+0,3S			0,08
		2,4		1,4	3,4	8,4+0,2S			0,09
		2,5		1,5	3,5	8,5+0,1S			0,10
		2,6		1,6	3,6	8,6+0,5S			0,06
		2,7		1,7	3,7	8,7+0,4S			0,07
		2,8		1,8	3,8	8,8+0,3S			0,08
		2,9		1,9	3,9	8,9+0,2S			0,09
		3,0		2,0	4,0	9,0+0,1S			0,10

Условие

Однородный каток В весом Q и радиусом R соединен гибкой нерастяжимой и невесомой нитью с грузом А весом Р (рис. 20). Нить переброшена через невесомый блок О радиусом r. К оси С катка (см. рис. 20, схемы 1–5) или к грузу А (см. рис.20, схемы 6–8) или к свободному концу нити (см. рис.20, схемы 9,10) приложена сила F, линейно зависящая от величины перемещения S. Каток катится без скольжения; коэффициент трения скольжения груза о плоскость равен f, момент сил сопротивления в подшипнике блока – М. Определить скорость груза А, когда он переместится на величину S. В начальный момент система находилась в покое.

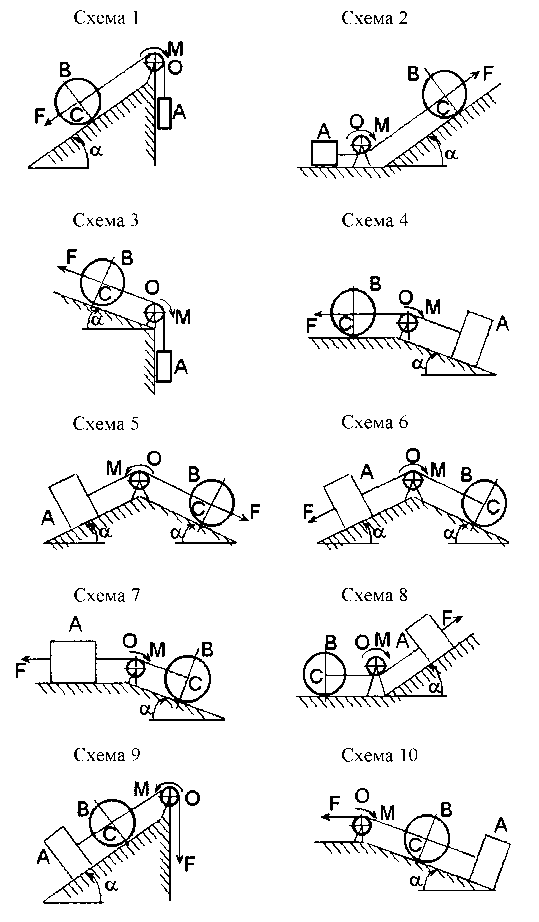
Рис. 20. Схемы к задаче 3.2

Пример решения задачи 3.2

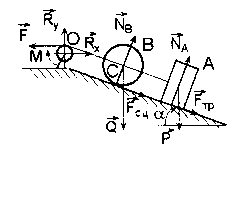Условие. Однородный каток В весом Q=4 кН и радиусом R и груз А весом Р=2 кН, соединенные гибкой нерастяжимой и невесомой нитью, помещены на шероховатую поверхность, наклоненную к горизонту под углом a=30⁰ (рис. 21). Нить переброшена через невесомый блок О радиусом 30 см. К свободному концу нити приложена сила F, линейно зависящая от величины перемещения s: F=9,0+0,15×s (кН). Каток катится без скольжения; коэффициент трения скольжения груза о плоскость f=0,1, момент сил сопротивления в подшипнике блока М=300 Н м. Определить скорость груза А, когда он переместится на величину s=3 м. В начальный момент система находилась в покое.

Рис. 21

Решение. Формула, выражающая теорему об изменении кинетической энергии механической системы в конечной (интегральной) форме, имеет вид

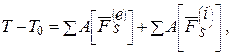(1)

где T, T₀ – кинетическая энергия системы соответственно в конечный и начальный моменты времени;

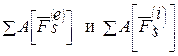– суммы работ соответственно всех внешних и внутренних сил, действующих в данной системе.

В рассматриваемой задаче система состоит из катка, груза, блока и нити. Система сил, действующих на систему, включает активные силы Q, P, F, реакции связей N_A, N_B, F_сц, F_тр, R_x, R_y и момент трения в блоке M.

Найдем сумму работ всех внешних сил системы на соответствующих перемещениях точек их приложения:

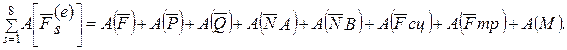
Работы сил N_А и N_B равны нулю, так как направления этих сил составляют прямой угол с направлениями перемещений точек их приложения. Работа силы сцепления F_сц и работы реакций R_x и R_у равны нулю, так как эти силы приложены к неподвижным точкам. Работы сил F, Р, Q, F_тр и пары сил с моментом М определим следующим образом:

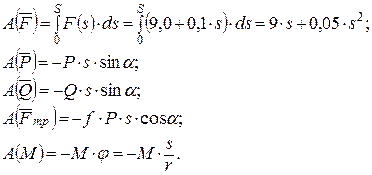
После суммирования получим

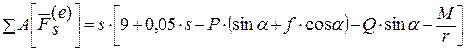. (2)

Рассматриваемая механическая система состоит из абсолютно твердых тел, соединенных идеальной нитью. Для таких систем с идеальными связями сумма работ всех внутренних сил равна нулю

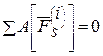. (3)

Рассчитаем кинетическую энергию системы в начальном и конечном положениях.

По условию задачи система в начальный момент находилась в покое, следовательно, ее кинетическая энергия в этот момент равна нулю T₀=0.

Кинетическая энергия груза А, движущегося поступательно, равна

,

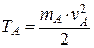где 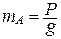– масса груза А; 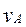– скорость груза.

Кинетическая энергия катка В, совершающего плоское движение, равна

,

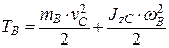где 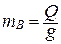– масса катка В;

v_C – скорость центра масс С катка, ;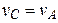

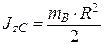– момент инерции катка относительно оси, проходящей через его центр масс;

w_В – угловая скорость катка, .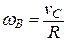

Кинетическая энергия системы равна сумме кинетических энергий всех тел, входящих в нее:

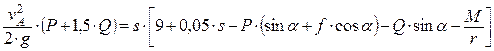. (4)

Подставляя выражения (2) – (4) в формулу (1), выражающую теорему об изменении кинетической энергии системы, получим

,

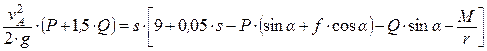откуда искомая скорость груза А, в момент, когда он переместится на расстояние 3 м, равна

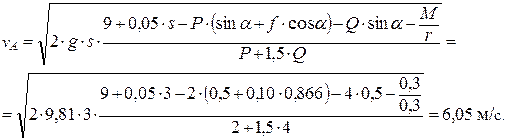
Задача 3.3

Задача решается с применением принципа Даламбера, позволяющего записать уравнения движения системы в форме уравнений равновесия. Для этого надо на схеме показать активные силы, реакции опор, силу инерции точечного груза и равнодействующую сил инерции стержня ED; составить уравнения равновесия плоской системы сил в выбранной системе координат и из решения этих уравнений найти требуемые величины. Исходные данные представлены в табл. 11.

Таблица 11

Цифра шифра	1-я цифра шифра	2-я цифра шифра	3-я цифра шифра
Длины, см	Силы, Н	Номер схемы (рис. 22)	a, град	n, об/мин
a	B	l1	l2	Q	P1	P2

Условие

К вертикальному валу весом Q жестко приварен невесомый стержень длиной l₁ с точечным грузом М весом Р₁ на конце и тонкий однородный стержень ED длиной l₂ весом Р₂, лежащие в одной плоскости (рис. 22). Определить реакции подпятника А и цилиндрического подшипника B, если вал вращается равномерно с частотой вращения n об/мин.

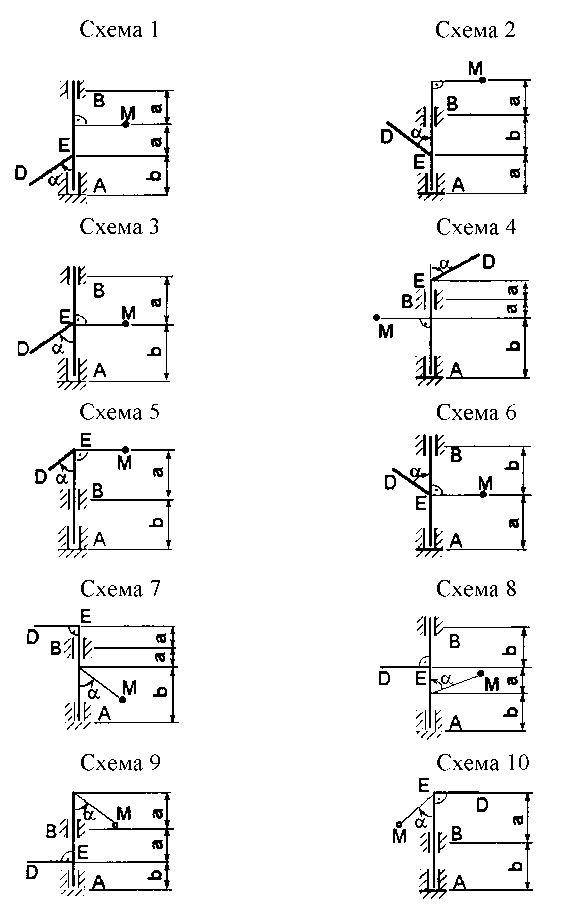
Рис. 22. Схемы к задаче 3.3
Пример решения задачи 3.3

Рис. 23

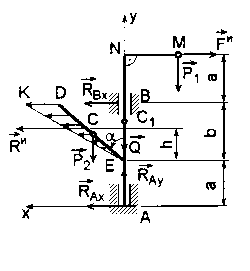
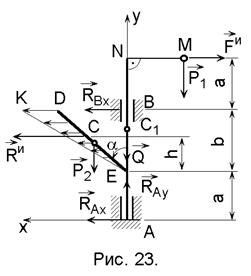Условие. К вертикальному валу весом Q=64 Н жестко приварен невесомый стержень длиной l₁=14 см с точечным грузом М весом Р₁=14 Н на конце и тонкий однородный стержень ED длиной l₂=28 см весом Р₂=28 Н, расположенные в одной плоскости (рис. 23). Определить реакции подпятника А и цилиндрического подшипника B, если вал вращается рав­номерно с частотой вращения n=300 об/мин, угол a=45⁰, a=44 см, b=58 см.

Решение. Введем вращающуюся вместе с валом систему координат Axy, как показано на рис. 23.

На вал действует плоская система сил: активные силы (Q, P₁, P₂), реакции подпятника А (R_Ax, R_Ay) и цилиндрического подшипника В (R_Bx). Введем в рассмотрение силы инерции Даламбера, которые присоединим к действующим на вал силам и введенным реакциям связей. Поскольку вал вращается с постоянной угловой скоростью, то касательные составляющие сил инерции равны нулю.

Центробежная сила инерции груза М равна

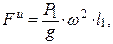
где 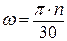– угловая скорость вала.

Сила инерции груза направлена в сторону, противоположную осестремительному ускорению точки М.

Для каждого элемента стержня ED массой Dm центробежная сила инерции определяется по формуле

,

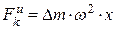где x – расстояние от элемента до оси вращения Ay.

Сила инерции элемента стержня направлена в сторону, противоположную осестремительному ускорению этого элемента.

Равнодействующая R^и этих распределенных по линейному закону параллельных сил проходит через центр тяжести треугольника EDK, на расстоянии 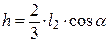и приводится к главному вектору сил инерции стержня ED

,

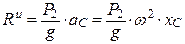где 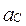– ускорение центра масс С стержня ED, x_С – абсцисса центра масс С стержня ED.

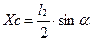
Полученная плоская система сил Q, P₁, P₂, R_Ax, R_Ay, R_By, F^и, и R^и в соответствии с принципом Даламбера является уравновешенной и для нее справедливы следующие уравнения равновесия:

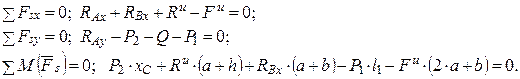
Решая эту систему трех уравнений с тремя неизвестными реакциями, получим

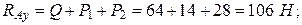
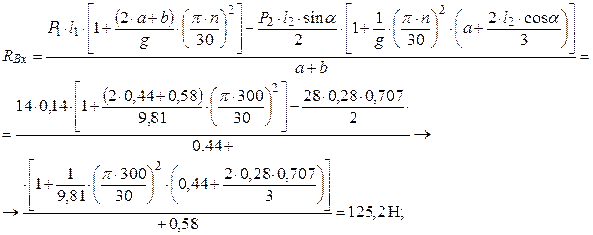
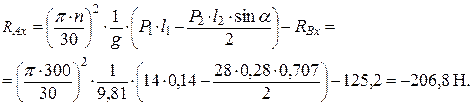
Знак минус, полученный в результате расчета реакции R_Ax, показывает, что истинное направление этой реакции противоположно указанному на рис. 23.

Для проверки правильности выполненного решения подсчитаем сумму моментов всех сил относительно любой точки (кроме использованной при составлении уравнений равновесия), например точки В:

;

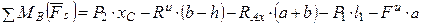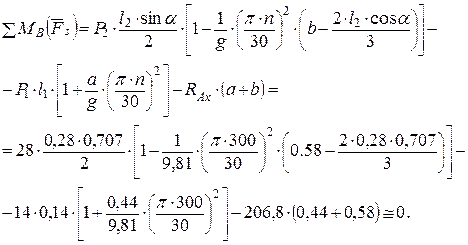
Полученный результат свидетельствует о правильности определения реакций.

Задания и методические указания к контрольным работам
по курсам "Теоретическая механика" и "Теоретическая и прикладная механика" Часть 1

Подписано в печать __.__.__. Формат 60х84/16. Бумага для множ. аппаратов. Печать плоская. Усл. печ. л. 2,63. Уч. - изд. л. 3,0. Тираж ___ экз. Заказ ___

Издательство Российского государственного профессионально-педагогического университета. Екатеринбург, ул. Машиностроителей, 11.

Ризограф РГППУ. Екатеринбург, ул. Машиностроителей, 11.