Принцип Даламбера (метод кинетостатики)

В каждый момент движения сумма активных сил, реакций связей и сил инерции равна нулю 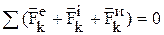— принцип Даламбера для материальной точки.

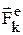– внешняя сила, 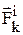– внутренняя сила. Сила инерции: 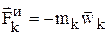, знак (–) показывает, что сила инерции направлена в противоположную сторону ускорению.

Для системы добавляется уравнение моментов: .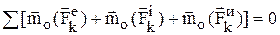

Обозначают: 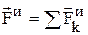– главный вектор сил инерции, 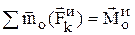– главный момент сил инерции. Учитывая, что геометрическая сумма внутренних сил и сумма их моментов равна нулю 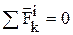, , 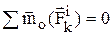получаем: 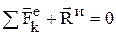, 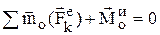— уравнения кинетостатики. Принцип Даламбера для системы – если в любой момент времени к каждой точке системы приложить, кроме реально действующих сил, соответствующие силы инерции, то полученная система сил будет находиться в равновесии и к ней можно применять уравнения статики. Это упрощает процесс решения задач.

Главный вектор сил инерции 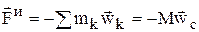равен произведению массы тела на ускорение его центра масс и направлен противоположно этому ускорению.

Главный момент сил инерции зависит от вида движения: при поступательном движении 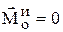; при плоском 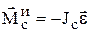, при вращении вокруг оси z, проходящей через центр масс тела, .

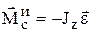Определение реакций при вращении твердого тела вокруг неподвижной оси.

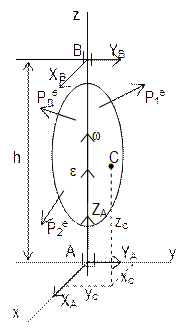При вращении тела вокруг неподвижной оси возникают динамические давления на опоры. Их определение удобно решать методом кинетостатики. Прикладываем силы инерции для каждой точки: центробежная 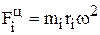, вращательная 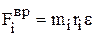, r_i– расстояние от точки до оси вращения. Проектируя сумму этих сил на оси и учитывая, что 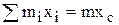и 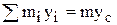, С – центр масс, получаем проекции главного вектора сил инерции:

, .

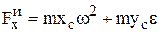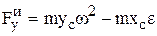Проекции главного момента сил инерции = сумме моментов центробежных и вращательных сил инерций относительно осей координат:

,

,

,

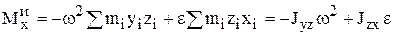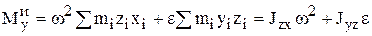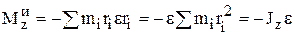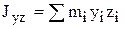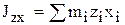, – центробежные моменты инерции,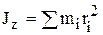

Учитывая внешние силы, можно записать уравнения равновесия кинетостатики:

,

,

,

,

,

.

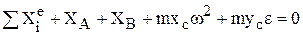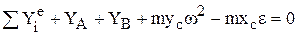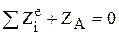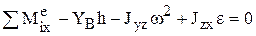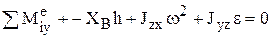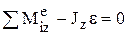Последнее уравнение не содержит реакций опор и представляет собой дифференциальное уравнение вращения тела. Остальные пять уравнений позволяют определить пять неизвестных реакций. Динамические составляющие реакций определяются слагаемыми, которые зависят от сил инерции.

Условия отсутствия динамических составляющих:

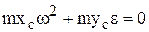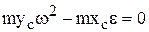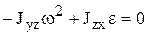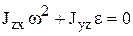, , , , откуда

x_C= 0, y_C= 0, J_yz= 0, J_zx= 0, это означает, что центр тяжести должен находиться на оси вращения тела и ось вращения тела z должна быть главной осью инерции тела. Т.е. ось вращения должна являться главной центральной осью инерции тела (ось, которая проходит через центр масс тела, и центробежные моменты инерции с индексом этой оси равны нулю). Для выполнения этого условия проводится специальная балансировка быстро вращающихся тел.