Определитель, содержащий нулевую строку. Перестановка строк

Перестановки и подстановки. Число перестановок из n символов. Транспозиция.

Перестановка порядка N – называется любое расположение первых n-натуральных чисел в некотором фиксированном порядке.

Теорема1: Число различных перестановок порядка n равно n!=1*2*3*…*(n-1)*n.

Док-во:

α₁ α₂ α_{3 ...} α_n

α₁ – n-способов

α₂ – (n-1)-способов

α₁* α₂ – n(n-1)-способов

α₁* α₂*α₃ – n(n-1)(n-2)-способов

n=3; 3!=1*2*3=6;

123; 132; 213; 231; 312; 321.

Транспозиция – если в некоторой перестановке поменять местами какие-либо два числа, а остальные оставить на месте, то мы получим новую перестановку.

n=5

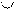2 3 1 4 5 2 4 1 3 5

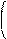
транспозиция

Теорема2:

Все n! перестановок из n чисел можно расположить в таком порядке, что каждая следующая будет получаться из предыдущей с помощью одной транспозиции.

Подстановкой n-го порядка, называется взаимнооднозначное отображение множества натуральных чисел от 1 до n на себя.

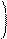1 2 3 ... n

α₁ α₂ α_{3 ...} α_n

Например:

1 2 3 4 5 1 5 3 4 2 2 1 3 4 5

3 4 5 1 2 3 2 5 1 4 3 4 5 1 2

Для подстановок справедливы теоремы 1-4.

Инверсия. Четность перестановки. Теорема о транспозиции и четности.

Инверсия – нарушение нормального порядка двух элементов в перестановке независимо от того, стоят ли эти два элемента рядом или отделены друг от друга какими-либо элементами.

α₁ α₂ α_{3 ...} α_i α_{j ...} α_n

Числа α_i и α_j образуют инверсию, если i<j, на α_i>α_j.

n=6

1 2 3 4 5 6 – 0 инверсий

3 2 1 4 5 6; 3 2, 3 1; 2 1; 4 1. 4 – инверсии, четная перестановка.

Если число инверсий чётное, то перестановка – чётная.

Если число инверсий нечётное, то перестановка – нечётная.

Теорема3:

Любая транспозиция меньше чётности перестановки.

Теорема4:

Число чётной перестановки из n-чисел равно числу нечётной равной n!/2

Определитель произвольного порядка. Определитель транспонированной матрицы.

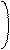
a₁₁ a₁₂ … a_1n

d

a₂₁ a₂₂ … a_2n

_{..........................}

a_n1 a_n2 … a_nn

Определителем n-го порядка – называется алгебраическая сумма n!-членов, которые представляют собой всевозможные произведения n-элементов матрицы, взятых по одному из каждой строки и столбца. Члены определителя берутся со знаком +, если его индексы составляют чётную подстановку и со знаком - если нечетную.

Транспортировать матрицу – строки сделать столбцами.

Определитель не меняется при транспонировании (det).

det A = det A^T

Док-во:

?

a₁₁ a₁₂ … a_1n a₁₁ a₁₂ … a_1n

a₂₁ a₂₂ … a_2n a₂₁ a₂₂ … a_2n

_{........................... ...........................}

a_n1 a_n2 … a_nn a_n1 a_n2 … a_nn

_{I II}

Любой член определителя I или вид. a_1α1 a_2α2 … a_nαn при чем все множители остаются в разных строках и разных столбцах, поэтому такое произведение также является и членом определителя II.

Определитель, содержащий нулевую строку. Перестановка строк.

Если одна из строк определителя состоит из нулей, то определитель равен 0.

Док-во: a_1α1*…* a_nαn

От перестановки двух строк у определителя меняется только знак

a₁₁ a₁₂ … a_1n

i a_j1 a_j2 … a_jn

j a_i1 a_i2 … a_in

a_n1 a_n2 … a_nn

i и j строки поменяем местами.

Получим определитель, который будет состоять из тех же членов, что и исходный определитель.

а_1αi *…* а_iαi*…* а_jαj*…* а_nαn

= φ1

1 α …i … j …n

α₁α_i…α_i…α_j…α_n

=φ2

1 α … j … i …n

α₁α_i…α_i…α_j…α_n

φ₁ и φ₂ – отличаются на одну транспозицию.