Умови існування різниці, її єдиність

Теорема про існування різниці цілих невід’ємних чисел: «Різниця цілих невід’ємних чисел а і b існує тоді і тільки тоді, коли b ≤ а».

Доведення.

1) Якщо а = b, то а – b = 0, тобто різниця а – b існує.

2) Якщо b < а, то за означенням відношення «менше» існує таке натуральне число с, що а = b + с. Тоді за означенням різниці с = а – b, тобто різниця а–b існує.

3) Якщо різниця а – b існує, то за означенням різниці існує таке ціле невід’ємне число с, що а = b + с. Якщо с = 0, то а = b; якщо с > 0, то b < а за означенням відношення «менше». Отже, b ≤ а.

Теорема про єдиність різниці цілих невід’ємних чисел: «Якщо різниця цілих невід’ємних чисел існує, то вона єдина».

Доведення. Нехай існують два значення різниці а – b: а – b = с₁ та а – b = с₂. Тоді за означенням різниці маємо а = b + с₁ та а = b + с₂. Звідси маємо в + с₁ = b + с₂, тому с₁ = с₂.

Правила віднімання

Правило віднімання числа від суми: «Щоб відняти число від суми, достатньо відняти його від одного з доданків та до отриманого результату додати інший доданок».

Дане правило сформулюємо символічно.

Якщо а, b, с – цілі невід’ємні числа, то:

1) при а ≥ с маємо, що (а + b) – с = (а – с) + b;

2) при b ≥ с маємо, що (а + b) – с = а + (b – с);

3) при а ≥ с та b ≥ с можемо використати будь-яку з даних рівностей.

Доведення (для випадку 1).

Нехай а ≥ с, тоді різниця а – с існує. Позначимо її буквою р, тобто а – с = р. Звідси а = р + с. Підставимо суму р + с замість а у вираз (а + b) – с та виконаємо перетворення: (а + b) – с = (р + с + b) – с = р + b. Але так як р = а – с, то (а + b) – с = = (а – с) + b, що й треба було довести.

Доведення для випадків 2 і 3 аналогічне.

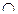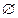Покажемо графічне зображення доведення даного правила за допомогою кругів Ейлера. Розглянемо три скінчені множини A, B та C такі, що n (A) =а, n (В) = b, n (С) = с, A B = та C 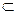A. Тоді (а + b ) – с – це кількість елементів множини (А 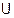В)\С, а число (а – с) + b – це кількість елементів множини (А\С) 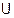В. На кругах Ейлера множина (А 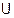В)\С зображена заштрихованою областю. Але множина (А\С) 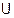В зображується такою ж самою областю. Тому (А 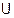В)\С = (А\С) 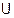В для даних множин А, В і С. Отже, n ((А 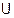В)\С) = n ((А\С) 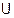В) та (а + b) – с = (а – с) + b.

Аналогічно можна показати графічне зображення для випадків 2 і 3.

Правило віднімання суми від числа: «Щоб від даного числа відняти суму, достатньо відняти від нього послідовно кожен доданок», тобто якщо а, b, с – цілі невід’ємні числа, то при а ≥ b + с маємо

а – (b + с) = (а – b) – с = (а – с) – в.

Доведення даного правила та його теоретико-множинне тлумачення за допомогою кругів Ейлера є аналогічними.

Дані правила в початковій школі розглядаються на конкретних прикладах при визначенні раціонального способу обчислення. Правило віднімання суми від числа є основою прийому віднімання по частинам:

12 – 5 = 12 – (2 + 3) = (12 – 2) – 3 = 10 – 3 = 7.

Також ці правила застосовуються при розв’язуванні задач різними способами. Наприклад задачу «На столі лежали 15 маленьких та 7 великих трикутників. Для аплікації використали 5 трикутників. Скільки трикутників залишилось?» можна розв’язати трьома способами:

1 спосіб: 1) 15 + 7 = 22 (тр.)

2) 22 – 5 = 17 (тр.)

2 спосіб: 1) 15 – 5 = 10 (тр.)

2) 10 + 7 = 17 (тр.)

3 спосіб: 1) 7 – 5 = 2 (тр.)

2) 15 + 2 = 17 (тр.).

5. Відношення «більше на», «менше на»

При розв’язуванні задач та в практичній діяльності буває необхідно не тільки визначити, що число а більше (або менше) числа b, але й дізнатися на скільки число а більше (або менше) числа b.

Встановимо теоретико-множинний смисл відношень «більше на» та «менше на». Нехай а і b – цілі невід’ємні числа такі, що а = n (А), b = n (В), причому а < b. Це означає, що у множині В можна виділити власну підмножину В₁, яка рівнопотужна множині А, та множина В\В₁ не є порожньою. Нехай n (В\В₁) = с, причому с ≠ 0. Тоді у множині В стільки ж елементів, що і у множині А, та ще с елементів. У цьому випадку кажуть, що число а менше числа b на с або число b більше числа а на с.

Так як с = n (В\В₁), де В₁ – підмножина множини В, то с = а–b.

Отже, щоб дізнатися, на скільки одне число більше або менше другого, треба від більшого числа відняти менше.

Відношення «більше на», «менше на» зустрічаються в простих текстових задачах з відношенням: це задачі на різницеве порівняння чисел, задачі на збільшення (зменшення) числа на декілька одиниць.

Задача 1: «На городі посадили 4 кущі малини та 9 кущів порічок. На скільки більше посадили кущів порічок?».

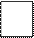
Згідно з правилом відповідь на питання задачі знаходимо за допомогою виразу на віднімання 9 – 4 = 5. Та чи можна від 9 кущів порічок відняти 4 кущі малини? Але в даному випадку від 9 кущів порічок віднімають 4 кущі порічок. Тож покажемо це, позначивши кущі малини кругами, а кущі порічок квадратами.

D

Z

Z₁

Щоб дати відповідь на питання задачі, виділимо у множині кущів порічок підмножину Z₁, рівнопотужну множині кущів малини. Тоді кущі порічок, що залишилися, утворюють доповнення множини Z₁ до множини Z та їх кількість дорівнює різниці чисел 9 і 4.

Задача 2: «На городі посадили 4 кущі малини, а кущів порічок на 5 більше. Скільки посадили кущів порічок?».

В цій задачі маємо дві множини: D – множина кущів малини, Z – множина кущів порічок. Відомо, що n (D) = 4, а кількість елементів множини Z треба знайти за умови, що в ній на 5 елементів більше, ніж у D. Тому n (Z) – n (D) = 5, звідки n (Z) = 5 + n (D) = 5 + 4 = 9.

Це також можна пояснити, спираючись на попереднє графічне зображення даних множин. Так як у множині Z на 5 елементів більше, ніж у множині D, а це означає, що у Z стільки ж елементів, скільки у D, та ще 5 елементів. Іншими словами, множину Z можна розглядати як об’єднання двох множин Z₁ і Z₂ таких, що Z₁~D та n (Z₂) = 5. Так як множини Z₁ і Z₂ не мають спільних елементів, то n (Z) = n (Z₁ 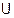Z₂) = n (Z₁) + n (Z₂) = 4 + 5 = 9.

Задача 3: «На городі посадили 9 кущів порічок, а малини на 3 кущі менше. Скільки кущів малини посадили?».

В цій задачі також маємо дві множини: множину кущів порічок (Z) та множину кущів малини (D), причому n (Z) = 9, а кількість елементів множини D треба знайти за умови, що в ній на 3 елемента менше, ніж у Z. Тому n (Z) – n (D) = = 3, звідки n (D) = n (Z) – 3 = 9 – 3 = 6.

Використовуючи наступне графічне зображення, розв’язання задачі здійснюється так: оскільки кущів малини на 3 менше, ніж кущів порічок, то кущів порічок на 3 більше, тому, видаливши із множини Z підмножину з трьох елементів, отримаємо множину, рівнопотужну множині D, тобто n (D) = 9 – 3 = 6.

Z

D

Тема. Текстова задача. Способи розв’язування текстових задач. Прийоми пошуку плану розв’язування текстових задач, способи запису і перевірки. Прості текстові задачі на додавання і віднімання

У початковому навчанні математики значну роль відіграють текстові задачі.

Під математичною задачеюрозуміють будь-яку вимогу обчислити, побудувати, довести що-небудь, що стосується кількісних відношень і просторових форм, створених людським розумом на основі знань про навколишній світ.

Арифметичною задачею називають вимогу знайти числове значення деякої величини, якщо дано числове значення інших величин і існує залежність, яка пов’язує ці величини як між собою, так і з шуканою.

У системі навчання учнів початкових класів загальноосвітньої школи переважають арифметичні задачі. Задачі на побудову, найпростіші доведення, а також завдання логічного порядку займають порівняно незначне місце. Задачі з одного боку становлять специфічний розділ програми, матеріал якого учні мають засвоїти, а з другого – виступають як дидактичний засіб навчання, виховання і розвитку школярів. Отже, задачі мають такі функції, як:

· пізнавальні, якими передбачаєтьсязасвоєння елементів арифметичної теорії: зміст арифметичних дій, властивості арифметичних дій, взаємозв’язок між результатом і компонентами арифметичних дій, кількісні відношення між числами;

· навчальні, які спрямовані на формування системи математичних ЗУН на різних етапах засвоєння;

· виховні, що дають змогу пов’язати навчання з життям, ознайомити учнів з пізнавально важливими фактами, сприяють розвитку в учнів свідоме ставлення до навчання;

· розвивальні,що спрямовані на формування в учнів науково – теоретичного (функціонального) стилю мислення, на оволодіння учнями прийомами розумової діяльності (аналізом, синтезом, конкретизацією, абстрагуванням, порівнянням, узагальненням), на висловлення власних суджень і міркувань.

У початкових класах, в основному, розглядають так звані сюжетні задачі, в яких описується кількісний бік якихось явищ, а знаходження невідомого зводиться до виконання певних арифметичних дій. В умові сюжетних задач подаються значення величин і деякі залежності (відношення) між цими значеннями, причому ці залежності мають певні числові характеристики.

Сюжетну задачу, для розв’язання якої треба виконати одну арифметичну дію, називають простою.

Сюжетну задачу називають складеною, якщо для її розв’язання виконують дві або більше арифметичних дій.

Структура текстової задачі:

· умова (числові значення величин і описання залежності між ними);

· питання (або вимога задачі – у наказовій формі формулювання);

· розв’язання;

· відповідь.

Вимоги до елементів задачі:

· умова задачі повинна містити реальні поняття та їх числові характеристики;

· умова задачі повинна бути логічно пов’язана із запитанням;

· повинні існувати наявні відношення між даними в умові;

· текст задачі лаконічний, правильно побудований з точки зору вимог мовлення.

Якщо завдання не відповідає якійсь з вимог до задач, його не вважають задачею. Наприклад:

1) Іван Царевич зірвав з першої яблуні 8 чарівних яблук, а з другої – 10. Скільки чарівних яблук зірвав Іван Царевич з третьої яблуні?

2) Мама купила 5 книжок. 2 книжки з’їли за обідом. Скільки книжок залишилося?

3) На дереві сиділо 8 риб, прилетіло ще 4. Скільки риб стало на дереві?

4) Скільки коштують 2 ляльки?

Етапи роботи над текстовою задачею:

1. Ознайомлення зі змістом задачі (читання вчителем, читання 1 учнем вголос, читання хором, самостійне читання учнями).

2. Бесіда за змістом задачі:

– Про що йдеться мова в задачі? (...)

– Що відомо? (...)

– Яке питання в задачі? (...)

3. Складання інтерпретації до задачі (порядкової, табличної, схематичної)

4. Повторення задачі вцілому.

5. Пошук розв’язання задачі.

6. Запис розв’язання і відповіді.

7. Творча робота над задачею.