Порядок структурного анализа плоского механизма

Установлен следующий порядок структурного анализа механизма:

- определение степени подвижности механизма (число степеней свободы);

- выделение структурных групп механизма;

- выделение механизма I класса;

- определение класса механизма.

Степень подвижности механизма W определяет число независимых параметров, которые необходимо задать механизму, чтобы движения всех звеньев механизма были определены, т. е. определяет число ведущих звеньев.

Группа, состоящая изведущего звена(или ведущих звеньев), соединенного кинематической парой со стойкой, должна иметь степень подвижности равную степени подвижности всего механизма.

Ведущее звено, соединённое со стойкой одной кинематической парой, условно называется механизмом I класса со степенью подвижности W= 1 (рис. 11).

W = 1

Рис. 11. Механизм I класса

Если к механизму I класса присоединить кинематическую цепь, то получится кинематическая схема механизма. При этом степень подвижности всего механизма не должна измениться.

Принцип образования механизмов, впервые сформулированный Л.В. Ассуром, заключается в следующем. Схема любого механизма может быть составлена последовательным присоединением к механизму I класса групп звеньев с нулевой степенью подвижности – групп Ассура.

Группой Ассура называется незамкнутая кинематическая цепь с нулевой степенью подвижности. Сколько бы групп Ассура ни присоединяли к механизму Iкласса, степень подвижности механизма остаётся равной единице.

Для плоского механизма, состоящего только из кинематических пар
5-го класса, степень подвижности групп Ассура определится согласно формуле Чебышева (2.1):

W = 3n – 2 p₅ = 0.(2.2)

Поскольку nи p₅ могут быть только целыми числами, из равенства (2.2) следует, что в группах Ассура возможны следующие сочетания количества звеньев и примыкающих к ним кинематических пар:

n = 2, p₅ = 3;

n = 4, p₅ = 6;

n = 6, p₅ = 9 и т. д.

На практике встречаются только первые два сочетания (рис. 12).

а) б)

Рис. 12. Примеры структурных групп Ассура

Разложение механизма на структурные группы необходимо для решения задач кинематического и динамического анализа, что обеспечит статическую определимость составляющих частей схем плоских механизмов.

Структурный анализ механизма следует проводить путем расчленения его на структурные группы в порядке, обратном образованию механизма. Выделение групп Ассура начинают с наиболее удаленной группы (последней в порядке присоединения к механизму I класса). В результате отсоединения структурных групп остается механизм I класса.

Класс группыАссура определяетсянаивысшим числом кинематических пар, примыкающих к замкнутому контуру, входящему в группу.

Класс механизма –наивысшим классом структурной группы, входящей в механизм.

Группы второго класса и второго порядка (n = 2,p₅ =3) делятся на 5 видов, которые определяются взаимным расположением вращательных и поступательных пар (рис. 13).

а) б)

в) г) д)

Рис. 13. Виды структурных групп II класса:

а) группа 1-го вида (все пары вращательные); б) группа 2-го вида (на конце одного из звеньев поступательная пара); в)группа 3-го вида (в середине поступательная пара); г)группа 4-го вида (на конце обоих звеньев поступательные пары); д)группа 5-го вида (в середине и на конце одного из звеньев поступательные пары)

Пример. Выполнить структурный анализ шарнирного механизма (рис. 14).

Рис. 14. Структурная схема шарнирного механизма

В соответствии с установленным порядком проведения структурного анализа:

1. Определяем степень подвижности механизма (число степеней свободы)

W = 3n – 2p₅ – p₄;

W = 3 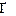3 – 2 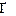4 – 0 = 1.

2. Выделяем структурную группу механизма – группу Ассура (последние два звена и три кинематических пары). Это группа II класса 1-го вида со степенью подвижности, равной

W = 3 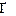2 – 2 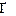3 – 0 = 0.

3. Выделяем механизм I класса (ведущее звено со стойкой). Его степень подвижности равна

W = 3 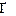1 – 2 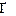1 – 0 = 1.

4. Определяем класс и порядок механизма.

В данном случае механизм образован присоединением группы Ассура II класса 1-го вида к механизму I класса. Этот механизм является механизмом II класса.